动态规划-斐波拉契数列笔记
@TOC

简介
Hello!
非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~
ଘ(੭ˊᵕˋ)੭
昵称:海轰
标签:程序猿|C++选手|学生
简介:因C语言结识编程,随后转入计算机专业,获得过国家奖学金,有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验:扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语!
唯有努力💪
算法知识点


算法题目来源
来源:leetcode.cn/
算法题目描述
斐波那契数,通常用 F(n) 表示,形成的序列称为斐波那契数列。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
给定 N,计算 F(N)。
示例 1:
输入:2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1.
示例 2:
输入:3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2.
示例 3:
输入:4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3.
提示:
- 0 ≤ N ≤ 30
做题思路
方法一:递归
从题目中可以看出,f(0)=0,f(1)=1,所以N<=1时,f(N)=N;N>1时,f(N)=f(N-1)+f(N-2)
那么可以很快写出下面的代码:
class Solution {
public:
int fib(int n) {
if(n <= 1) return n;
return fib(n-1) + fib(n-2);
}
};
运行结果

上面代码是一个基础的递归写法。对于递归,海轰有这种感受:看到答案后,这题太简单了吧;只看题目,emm,太难,大概知道方法是啥,但就是写不出代码!
初学递归时,最难的就是无法知道程序具体是如何运行的?每一步干啥了?
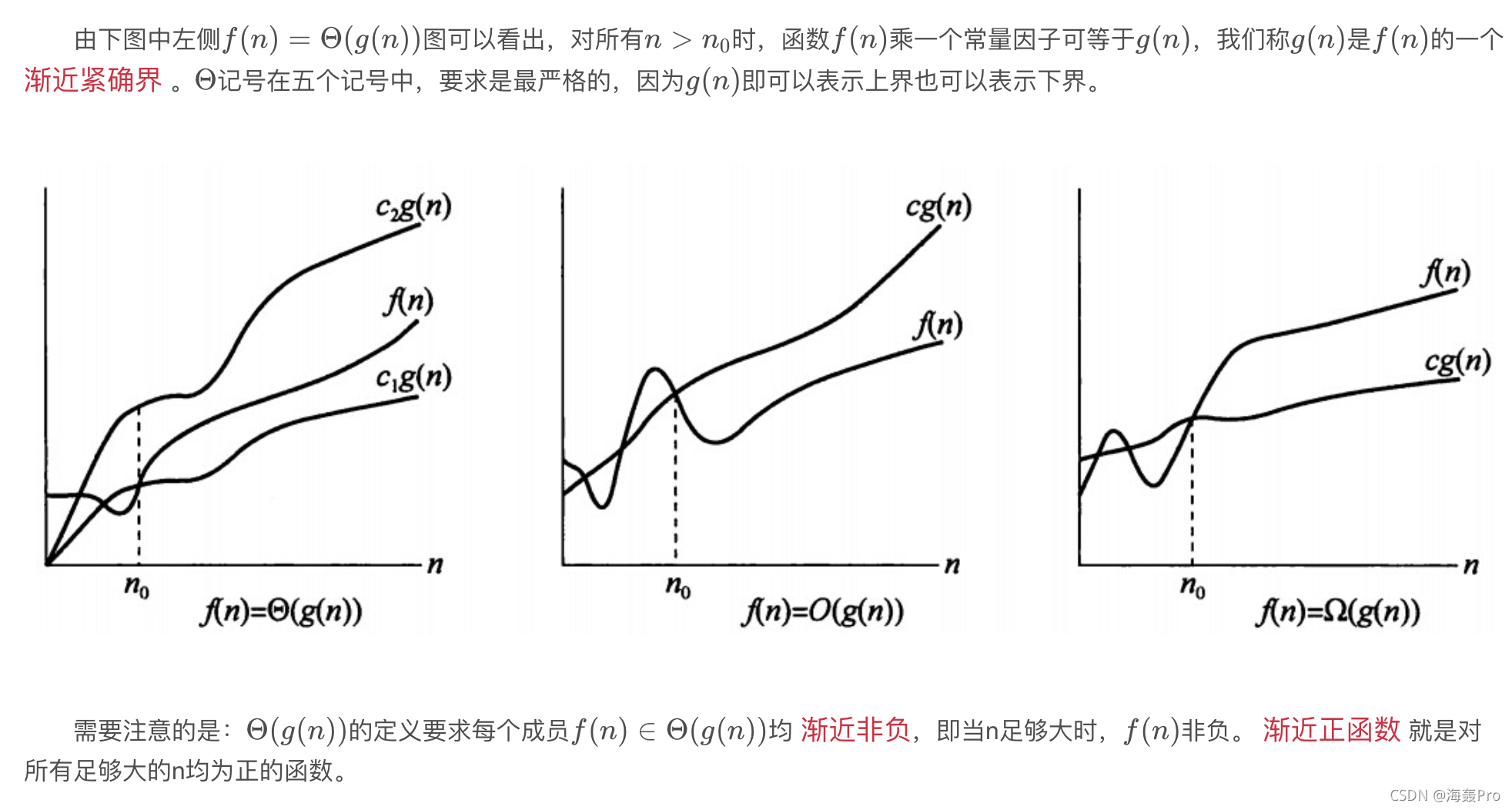
笨鸟先飞!既然咱们的大脑想不出,那就动手模拟程序的运行过程,想象自己就是计算机,运行一次代码。这里我们假设需要计算f(4),得到如下的程序运行图:
从图中我们可以发现:首先进入fib函数时,N=4,发现不满足N<=1的条件,那么就运行return 语句,而运行retun fib(3)+fib(2),首先需要计算fib(3),那么进而转入下一个fib函数,此时N=3,发现不满足N<=1,那么就运行return, 而运行return f(2)+f(1),又需要计算f(2),那么又转了下一个fib函数,此时N=2…
按照上图的路径跑一下f(4)是如何计算出的,那么对于f(N)的一般过程我们也就可以懂了。开始的时候觉得这样画图很浪费时间,没有必要,但是每次遇到递归时,都需要思考很久,因为不知道具体程序如何运行,特别是二叉树那里!多画了几次后,渐渐也懂了递归的思想,简单题慢慢也可以做出了。
方法二:利用辅助数组
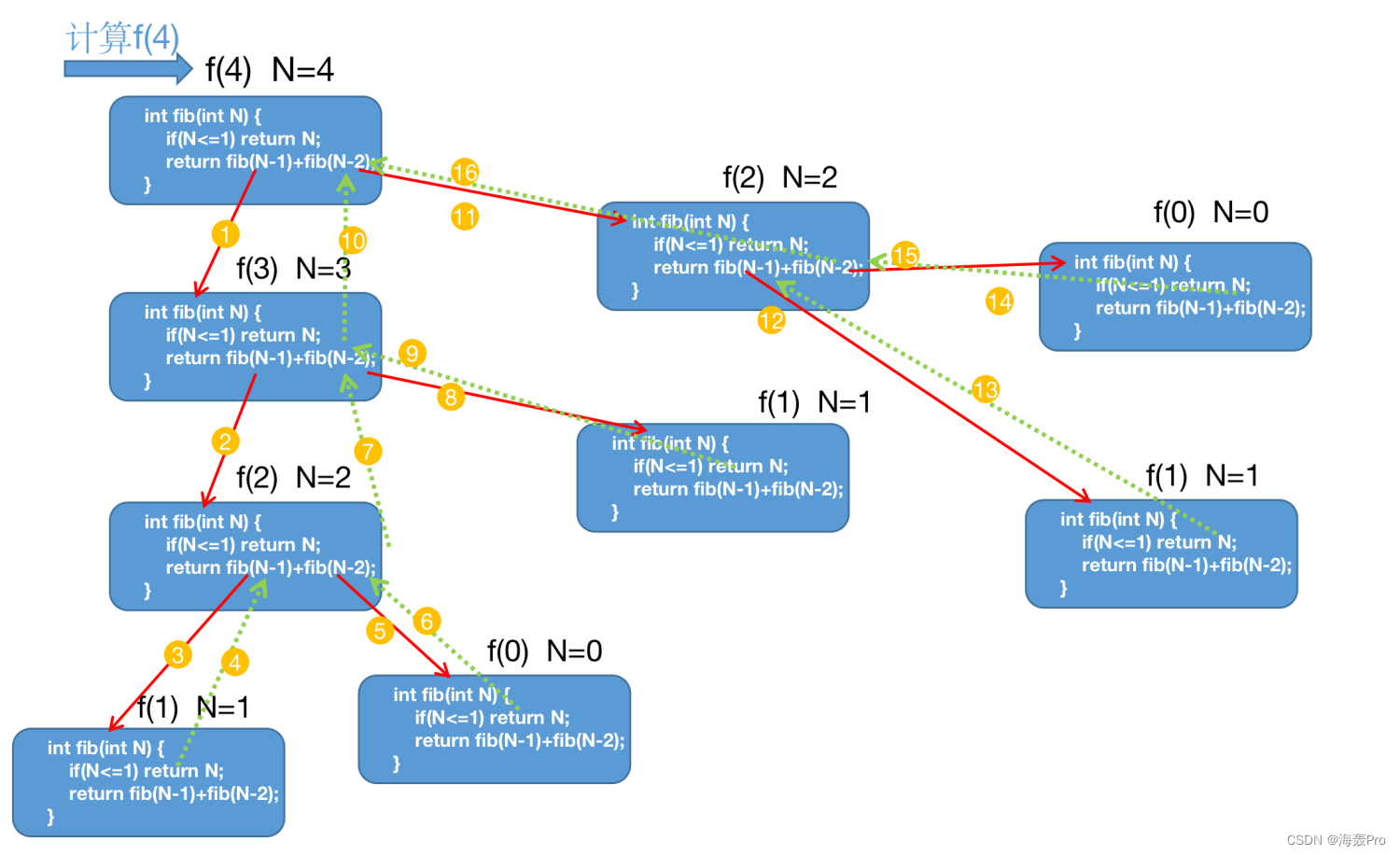
将上面的图简化,得到下图。
我们可以发现使用方法一,我们做了非常多的无用功:比如计算f(4)时,我们需要算出f(2),而在计算f(3)时,我们又需要计算f(2)…当N非常大的时候,这样的重复计算就会浪费非常多的时间。
那么有什么办法可以解决这个问题呢?
假设第一次计算出f(2)后,我们将它保存在数组中,下一次需要用到f(2)时,我们直接从数组中提取。这样一来,每个f(n)就只计算了一次,大大提高了运行效率。
编写代码如下:(递归+全局辅助数组)
// 定义全局辅助数组,因为由题目已知最大N=30,那么数组长度最多为31,初始化都为-1,
// 计算出一个f值,填入对应数组中的一个元素
// 每次先测试对应数组中的元素,如果为-1,表示尚未计算,需要进行第一次的计算
// 如果不为-1 表示已经计算过了 直接提取即可
// 假设我们需要f(10),首先看看a[10]是否为-1,如果a[10]=-1,则需要计算f(10)
// 反之 直接提取a[10]中的值即可
vector<int> a= vector<int> (31,-1);
int fib(int N)
{
if (N <= 1)
return N;
// 如果已经计算过 则直接返回存在数组中的值
if (a[N] != -1)
return a[N];
// 若没有 则需要计算出 并保存在相应的位置
a[N] = fib(N - 1) + fib(N - 2);
return a[N];
}
运行结果

在上面的代码中,海轰使用了全局辅助数组来存储f(n)。不知道细心的小伙伴发现没有,数组a的长度这里是直接采用的N的最大值+1。题目中N<=30,但假设N=10000时,我们每次都生成长度为10001长度的数组,那么在计算f(3)、f(10)…的时候,会造成非常大的空间浪费。
优化方案:动态分配,根据N的大小,每次固定分配N+1的空间(生成长度为N+1的数组)
改进后编写代码如下:(递归+辅助数组)
int help(vector<int> &a,int N){
if(N<=1) return N;
if(a[N]!=-1) return a[N];
a[N]=help(a,N-1)+help(a,N-2);
return a[N];
}
int fib(int N)
{
vector<int> a(N+1,-1);//每次生成数组的长度永远都是N+1 动态变化
return help(a,N);
}
运行结果

方法三:动态规划
在方法二中,我们可以发现,计算f(20)时,需要先计算f(19)【注:f(20)=f(19)+f(18),代码中是return f(n-1)+f(n-2),所以会需要先计算f(19),f(19)计算完成后,再计算f(18)】;计算f(19)时,需要先计算f(18)…可以发现程序计算的顺序是:20->19->18->17… 从顶向下的。
那么是否可以反过来?从底向上呢?答案是:可以的。
通过表达式f(N)=f(N-1)+f(N-2)可得,一个表达式的值是由前面两个表达式决定的【f(0)、f(1)除外】。假设我们求f(4),由已知:f(0)=0 f(1)=1, 可以求得 f(2)=f(1)+f(0)=1+0=1 f(3)=f(2)+f(1)=1+1=2 f(4)=f(3)+f(2)=3。这样不就是从底向上求得结果了吗?【哈哈,其实仔细想想,这不就是我们平时自己的思路吗】
那么如何模拟这种思路呢?这里我们依然借助一个数组a,长度为N+1【为啥长度是N+1?假设N=4,那么我们需要计算f(0)、f(1)、f(2)、f(3)、f(4),需要长度为5的数组存储每一个f(n)】
首先f(0)=0 f(1)=1是已知的,也就有:a[0]=1 a[1]=1,然后依次计算f(2)、f(3)…
以f(2)计算为例:
f(2)=f(1)+f(0)=1+0=1
计算出后,立马存入a[2]:a[2]=1
计算f(3)时 如果用f(3)=f(2)+f(1),这里f(2)是未知的哦
但是还记得我们在数组中存储了f(2)吧 也就是a[2]
所以
f(3)=a[2]+a[1]
依次类推 得出规律
a[n]=a[n-1]+a[n-2] // 需要求f(n) ,仔细想想,是不是就是求a[n]
编写代码如下:(自底向上)
class Solution {
public:
int fib(int N)
{
// N<2 直接返回N
if(N<=1) return N;
// N>=2时
// 利用一个辅助数组,存下N对应于数组中的值
// 比如 算出f(2)=1后,令a[2]=1 便于后面的运算
vector<int> a(N+1,0);
a[0]=0;
a[1]=1;
for(int i=2;i<=N;++i){
a[i]=a[i-1]+a[i-2];
}
return a[N];
}
};
运行结果

思考:
不知道有小伙伴发现没有,其实每次参与运算的变量其实就两个:一个f(n),一个f(n-1),以f(7)为例:f(2)=f(1)+f(0)–>f(3)=f(2)+f(1)–>f(4)=f(3)+f(2)… f(7)=f(6)+f(5)
优化:
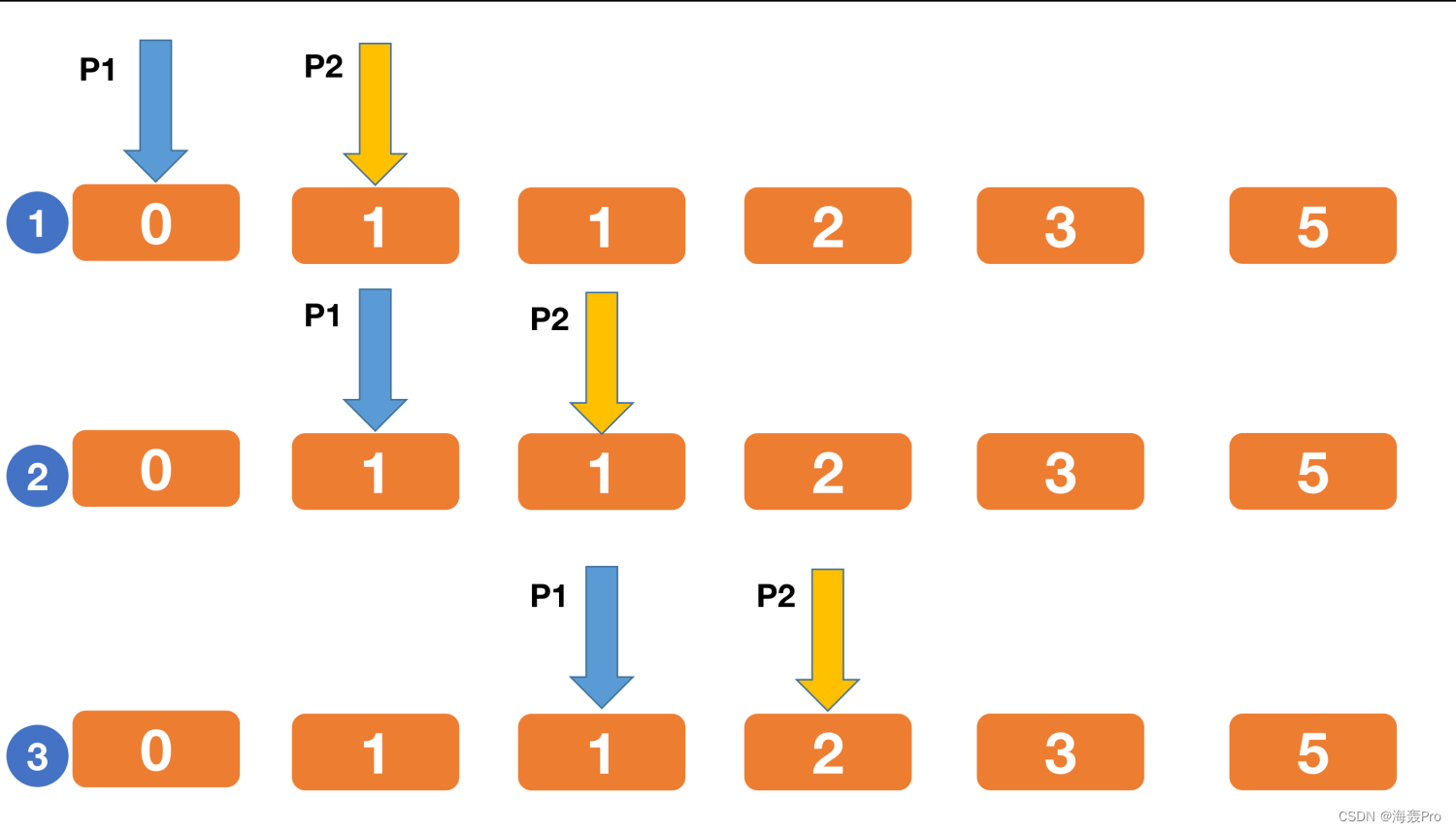
我们可以使用两个变量P1、P2,其中P1是左边较小,P2是右边较大的。
初始化:P1=0 P2=1
两个指针分别更新:P2=P2+P1 P1=P2(这里的P2是指原来的P2=1,不是与P1相加后的P2,所以需要一个临时变量存储原来的P2)
移动规则:
temp=P2
P2=P2+P1;
P1=temp;
编写代码如下:
int fib(int N)
{
if(N<=1) return N;
int p1=0;
int p2=1;
for(int i=2;i<=N;++i){
int temp=p2;
p2+=p1;
p1=temp;
}
return p2;
}
运行结果

注:优化后性能确实会提升,上图仅为某一次运行截图
方法四:矩阵求幂
由数学可得:斐波那契数列矩阵方程
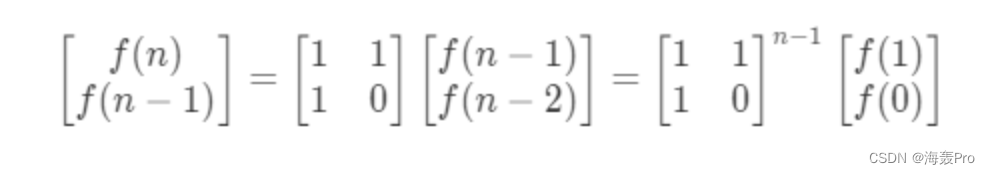
方程解释如下:

编写代码如下:
int fib(int N)
{
if(N<=1) return N;
int A[2][2]={
{1,1},
{1,0}};
martixpower(A,N-1);// 求 A矩阵的n-1次方
return A[0][0];// 从上面公式证明可以看出,答案就是n-1方中结果的[0][0]项
}
// 计算矩阵A的n-1次方
void martixpower(int A[2][2],int N){
int B[2][2]={
{1,1},
{1,0}
};
// 利用循环 模拟n-1次方
for(int i=0;i<N-1;++i){
multiply(A,B);
}
}
// 矩阵乘法 A*B
void multiply(int A[2][2],int B[2][2]){
int x = A[0][0] * B[0][0] + A[0][1] * B[1][0];
int y = A[0][0] * B[0][1] + A[0][1] * B[1][1];
int z = A[1][0] * B[0][0] + A[1][1] * B[1][0];
int w = A[1][0] * B[0][1] + A[1][1] * B[1][1];
A[0][0] = x;
A[0][1] = y;
A[1][0] = z;
A[1][1] = w;
}
运行结果

思考:
假设我们需要求
=?
使用for循环:333…33 ,那么将会做99次乘法
但从另一个角度思考:
=
:如果知道
那么再与自身相乘就可以得
,需要一次乘法
=
…
通过上面我们可以发现
–>
–>
–>
–>
–>
…
总结:通过1次方可以求出2次方,2次方可以求出4次方,4次方可以求出8次方…
所以,利用递归,求A的N-1次方代码如下:(这里求矩阵的N-1次方也用到了递归哦 小伙伴可以试试 会有收获的)
int fib(int N)
{
if(N<=1) return N;
int A[2][2]={
{1,1},
{1,0}};
martixpower(A,N-1);// 求 A矩阵的n-1次方
return A[0][0];
}
// 递归求N-1次方
void martixpower(int A[2][2],int N){
if(N<=1) return;
martixpower(A,N/2);// 求A矩阵的(n-1)/2 次方
multiply(A,A); 求的(n-2)/次方后 再与自身相乘
// 如果N是奇数 则还需要在乘一次B
if(N%2==1){
int B[2][2]={
{1,1},
{1,0}
};
multiply(A,B);
}
}
void multiply(int A[2][2],int B[2][2]){
int x = A[0][0] * B[0][0] + A[0][1] * B[1][0];
int y = A[0][0] * B[0][1] + A[0][1] * B[1][1];
int z = A[1][0] * B[0][0] + A[1][1] * B[1][0];
int w = A[1][0] * B[0][1] + A[1][1] * B[1][1];
A[0][0] = x;
A[0][1] = y;
A[1][0] = z;
A[1][1] = w;
}
测试结果

方法五:公式法
对于斐波那契数列,通项公式如下:
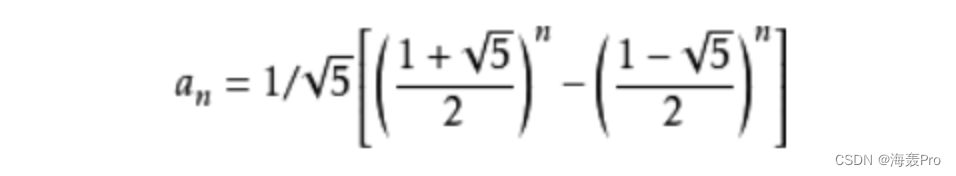
通过公式编写代码如下:
int fib(int N)
{
double goldenRatio = (1 + sqrt(5)) / 2;
double goldenRatiox=(1-sqrt(5))/2;
return (int)round((pow(goldenRatio, N)-pow(goldenRatiox,N))/ sqrt(5));
}
测试结果

但是力扣官方给出的代码如下:
int fib(int N)
{
double goldenRatio = (1 + sqrt(5)) / 2;
return (int)round(pow(goldenRatio, N)/ sqrt(5));
}
开始看代码的时候,总觉得官方代码少了一部分,但计算结果还能对,非常神奇!
仔细观察发现二者的区别在于:后者省略了(1-
)/2 的n次方。
那么为什么可以简化为官方那样的代码呢?
通过计算:
(1-
)/2 的0次方=1
(1-
)/2 的1次方=-0.618(黄金分割比)
(1-
)/2 的2次方=0.3819
(1-
)/2 的3次方=-0.2360
(1-
)/2 的4次方=0.1458
(1-
)/2 的5次方=-0.0901
(1-
)/2 的6次方=0.0557
我们发现:随着n的增大,(1-
)/2 的n次方也越来越趋近于0,之后可忽略不计。n较小时,我们利用round函数(四舍五入取整)即可,这样是可以达到和原公式规整代码一样结果的。
模板代码
int fib(int N)
{
if(N<=1) return N;
int A[2][2]={
{1,1},
{1,0}};
martixpower(A,N-1);// 求 A矩阵的n-1次方
return A[0][0];
}
// 递归求N-1次方
void martixpower(int A[2][2],int N){
if(N<=1) return;
martixpower(A,N/2);// 求A矩阵的(n-1)/2 次方
multiply(A,A); 求的(n-2)/次方后 再与自身相乘
// 如果N是奇数 则还需要在乘一次B
if(N%2==1){
int B[2][2]={
{1,1},
{1,0}
};
multiply(A,B);
}
}
void multiply(int A[2][2],int B[2][2]){
int x = A[0][0] * B[0][0] + A[0][1] * B[1][0];
int y = A[0][0] * B[0][1] + A[0][1] * B[1][1];
int z = A[1][0] * B[0][0] + A[1][1] * B[1][0];
int w = A[1][0] * B[0][1] + A[1][1] * B[1][1];
A[0][0] = x;
A[0][1] = y;
A[1][0] = z;
A[1][1] = w;
}
结语
文章仅作为个人学习笔记记录,记录从0到1的一个过程
希望对您有一点点帮助,如有错误欢迎小伙伴指正

- 点赞
- 收藏
- 关注作者


评论(0)