图的遍历 深度和广度遍历算法

#include"stdio.h"
#include"stdlib.h"
#define MaxVertexNum 100     //定义最大顶点数
typedef struct {
	char vexs[MaxVertexNum];        //顶点表
	int edges[MaxVertexNum][MaxVertexNum];   //邻接矩阵，可看作边表
	int n, e;          //图中的顶点数n和边数e
}MGraph;              //用邻接矩阵表示的图的类型
//建立邻接矩阵
void CreatMGraph(MGraph *G)
{
	int i, j, k;
	char a;
	printf("Input VertexNum(n) and EdgesNum(e): ");
	scanf("%d,%d", &G->n, &G->e);         //输入顶点数和边数
	scanf("%c", &a);
	printf("Input Vertex string:");
	for (i = 0; i < G->n; i++)
	{
		scanf("%c", &a);
		G->vexs[i] = a;             //读入顶点信息，建立顶点表
	}
	for (i = 0; i < G->n; i++)
		for (j = 0; j < G->n; j++)
			G->edges[i][j] = 0;    //初始化邻接矩阵
	printf("Input edges,Creat Adjacency Matrix\n");
	for (k = 0; k < G->e; k++) {       //读入e条边，建立邻接矩阵  
		scanf("%d%d", &i, &j);        //输入边（Vi，Vj）的顶点序号
		G->edges[i][j] = 1;
		G->edges[j][i] = 1;
		//若为无向图，矩阵为对称矩阵;若建立有向图，去掉该条语句 
	}
}
//定义标志向量，为全局变量
typedef enum { FALSE, TRUE } Boolean;
Boolean visited[MaxVertexNum];
//DFS：深度优先遍历的递归算法
void DFSM(MGraph *G, int i)
{ //以Vi为出发点对邻接矩阵表示的图G进行DFS搜索，邻接矩阵是0，1矩阵
	int j;
	printf("%c", G->vexs[i]);     //访问顶点Vi
	visited[i] = TRUE;             //置已访问标志
	for (j = 0; j < G->n; j++)          //依次搜索Vi的邻接点
		if (G->edges[i][j] == 1 && !visited[j])
			DFSM(G, j);  //（Vi，Vj）∈E，且Vj未访问过，故Vj为新出发点
}
void DFS(MGraph *G)
{
	int i;
	for (i = 0; i < G->n; i++)
		visited[i] = FALSE;            //标志向量初始化
	for (i = 0; i < G->n; i++)
		if (!visited[i])              //Vi未访问过
			DFSM(G, i);               //以Vi为源点开始DFS搜索
}
//BFS：广度优先遍历
void BFS(MGraph *G, int k)
{         //以Vk为源点对用邻接矩阵表示的图G进行广度优先搜索
	int i, j, f = 0, r = 0;
	int cq[MaxVertexNum];        //定义队列   
	for (i = 0; i < G->n; i++)
		visited[i] = FALSE;	         //标志向量初始化
	for (i = 0; i < G->n; i++)
		cq[i] = -1;                    //队列初始化
	printf("%c", G->vexs[k]);     //访问源点Vk
	visited[k] = TRUE;
	cq[r] = k;          //Vk已访问，将其入队。注意，实际上是将其序号入队
	while (cq[f] != -1) {          //队非空则执行
		i = cq[f]; f = f + 1;             //Vf出队
		for (j = 0; j < G->n; j++)         //依次Vi的邻接点Vj
			if (G->edges[i][j] == 1 && !visited[j]) {  //Vj未访问
				printf("%c", G->vexs[j]);         //访问Vj
				visited[j] = TRUE; 		         r = r + 1; cq[r] = j;          //访问过Vj入队
			}
	}
}
//main
void main()
{
	int i;
	MGraph *G;
	G = (MGraph *)malloc(sizeof(MGraph));   //为图G申请内存空间
	CreatMGraph(G);          //建立邻接矩阵
	printf("Print Graph DFS: ");
	DFS(G);                  //深度优先遍历
	printf("\n");
	printf("Print Graph BFS: ");
	BFS(G, 3);             //以序号为3的顶点开始广度优先遍历
	printf("\n");
}


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
 

举例：

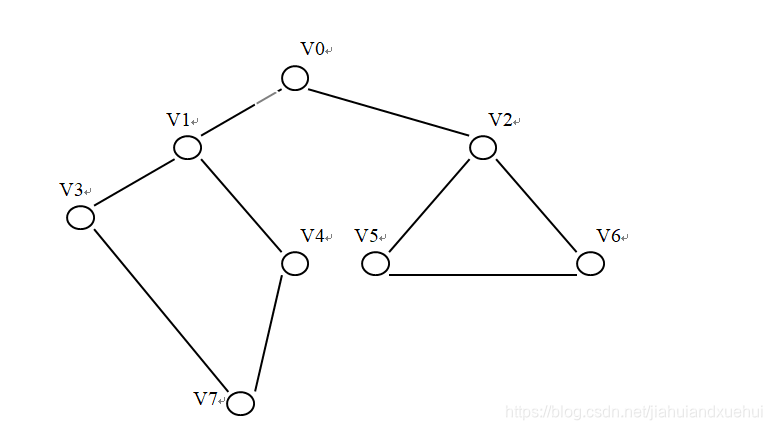
执行顺序：
Input VertexNum(n) and EdgesNum(e): 8，9
Input Vertex string: 01234567
Input edges,Creat Adjacency Matrix
0 1
0 2
1 3
1 4
2 5
2 6
3 7
4 7
5 6
Print Graph DFS: 01374256
Print Graph BFS: 31704256

文章来源: blog.csdn.net，作者：肥学，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/jiahuiandxuehui/article/details/110485592