图的二种遍历-广度优先遍历和深度优先遍历
图的广度优先遍历
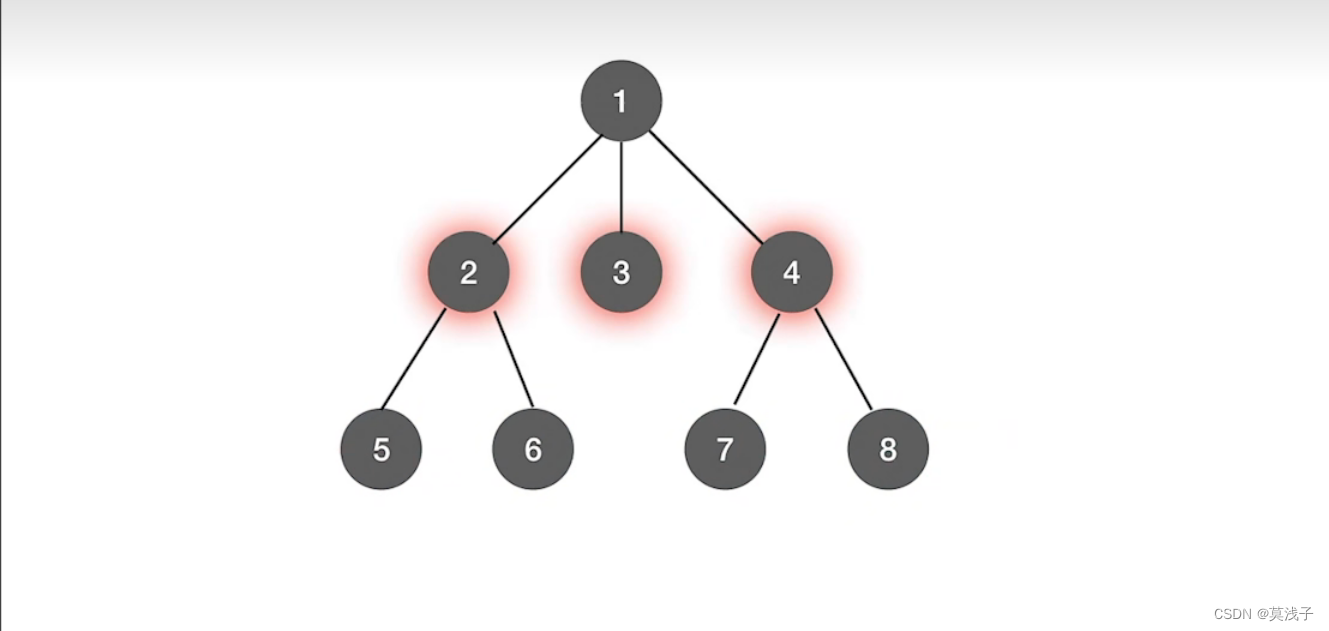
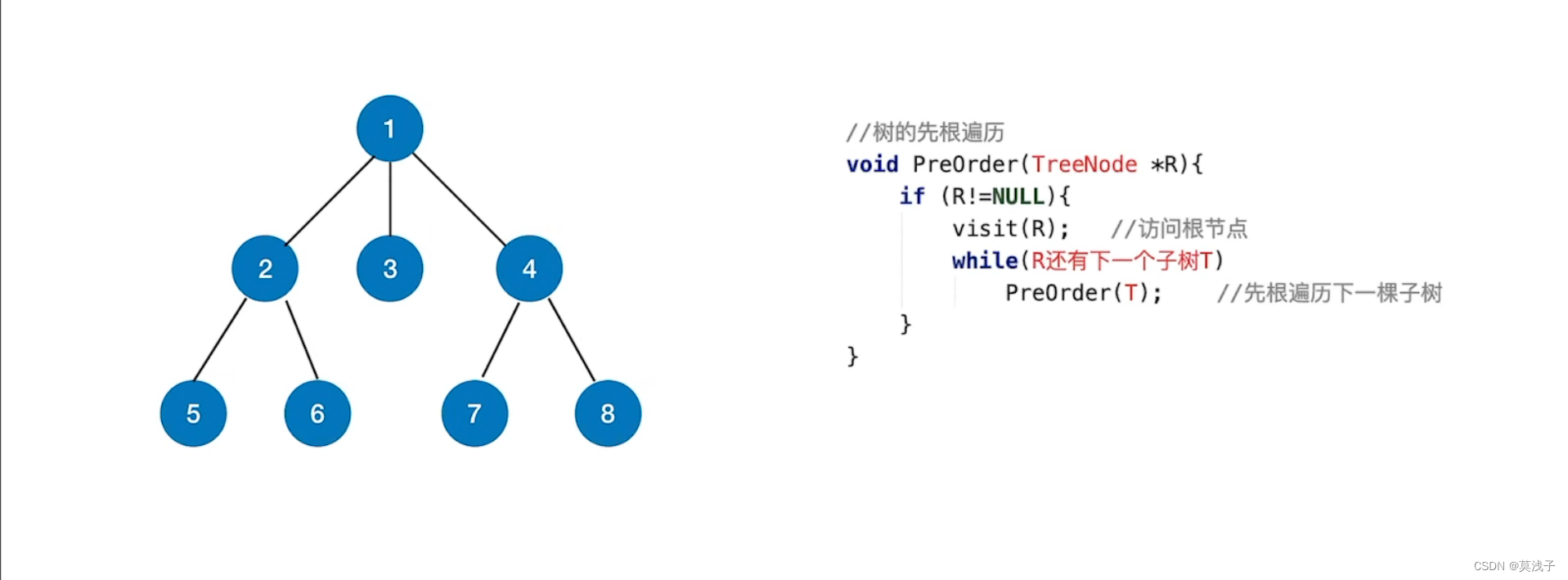
1.树的广度优先遍历
这样一个图中，是如何实现广度优先遍历的呢，首先，从1遍历完成之后，在去遍历2,3,4，最后遍历5 ，6 , 7 , 8。这也就是为什么叫做广度优先遍历，是一层一层的往广的遍历
不存在“回路”，搜索相邻的结点时，不可能搜到已经访问过的结点
树的广度优先遍历（层序遍历)
①若树非空，则根节点入队
②若队列非空，队头元素出队并访问，同时将该元素的孩子依次入队
③重复②直到队列为空
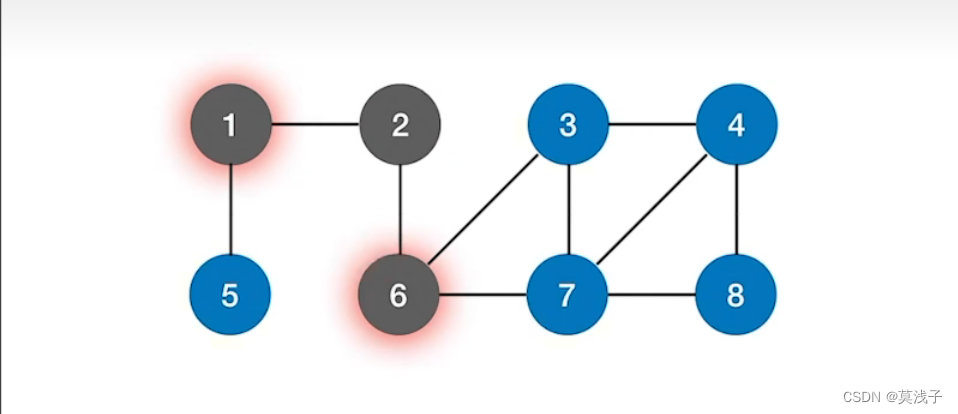
2.图的广度优先遍历
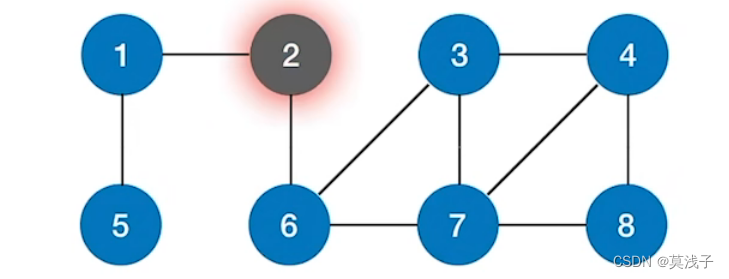
图的广度优先和树的广度优先还是非常相似的，首先我们假设我们从 2 号结点开始，然后广度优先遍历 1 , 6 （这里面1和6的顺序无所谓，但是还是为了保持一定的顺序，一般从小的开始）然后1的话再遍历就是5 ， 6再找相邻的就是 3 和 7 ，于是访问的就是 5 ，3 ，7 。在找到下一层就是 4 ，8 。
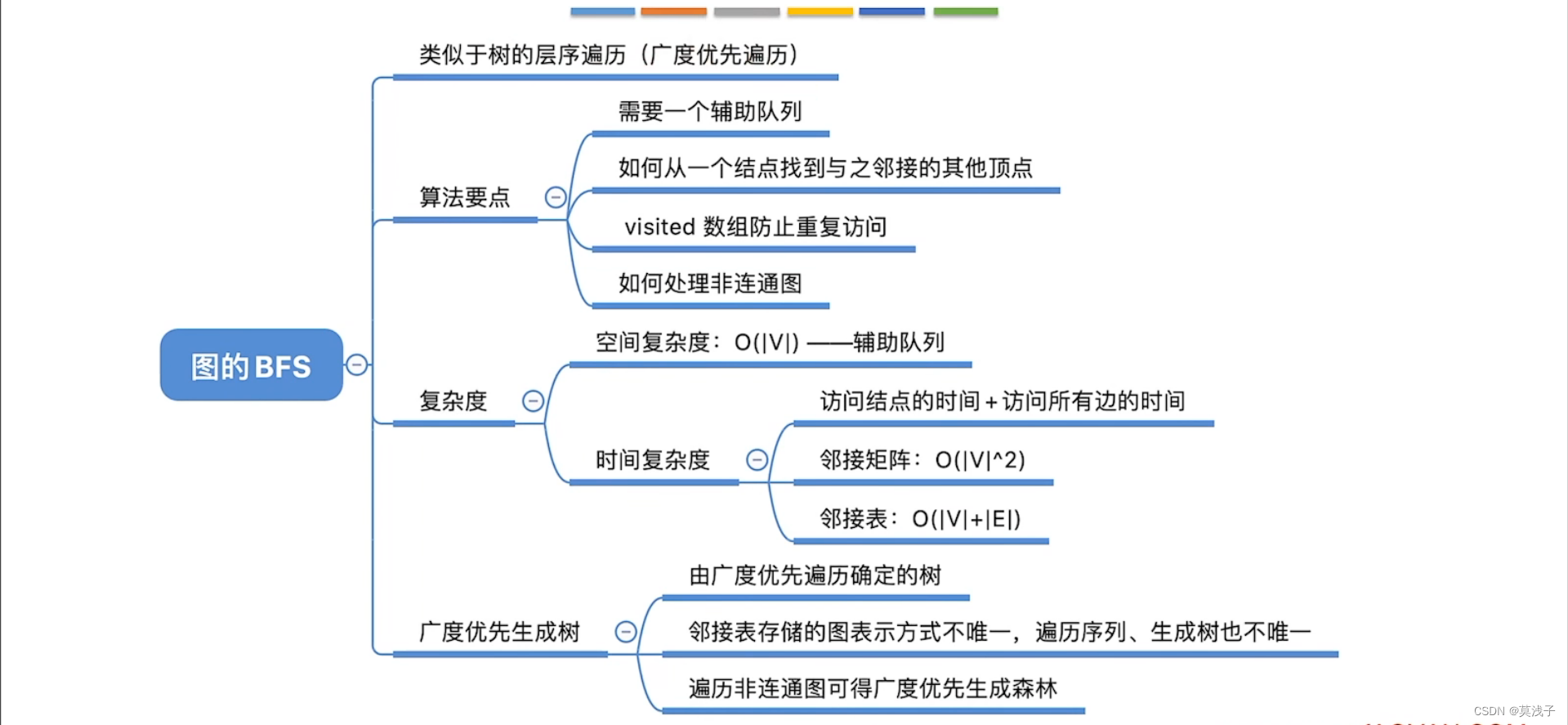
广度优先遍历(Breadth-First-Search, BFS)要点:
1．找到与一个顶点相邻的所有顶点·
2、标记哪些顶点被访问过
3．需要一个辅助队列
FirstNeighbor(G,x):求图G中顶点x的第一个邻接点，若有则返回顶点号。若x没有邻接点或图中不存在x，则返回-1。
NextNeighbor(G,x,y)︰假设图G中顶点y是顶点x的一个邻接点，返回除y之外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1。
代码
bool visited [MAX_VERTEX_NUM];/访问标记数组
//广度优先遍历
void BFS( Graph G,int v){//从顶点v出发，广度优先遍历图G
visit(v); //访问初始顶点v
visited [v]=TRUE; //对v做已访问标记
Enqueue(Q,v); //顶点v入队列Q
while( !isEmpty(Q) ){
DeQueue(Q, v); //顶点v出队列
for(w=FirstNeighbor(G,v ) ;w>= ; w=NextNeighbor(G,v,w))
//检测v所有邻接点
if( !visited [w] )//w为v的尚未访问的邻接顶点
{
visit(w);//访问顶点w
visited [w]=TRUE;//对w做已访问标记
EnQueue(Q,w);//顶点w入队列
}
}
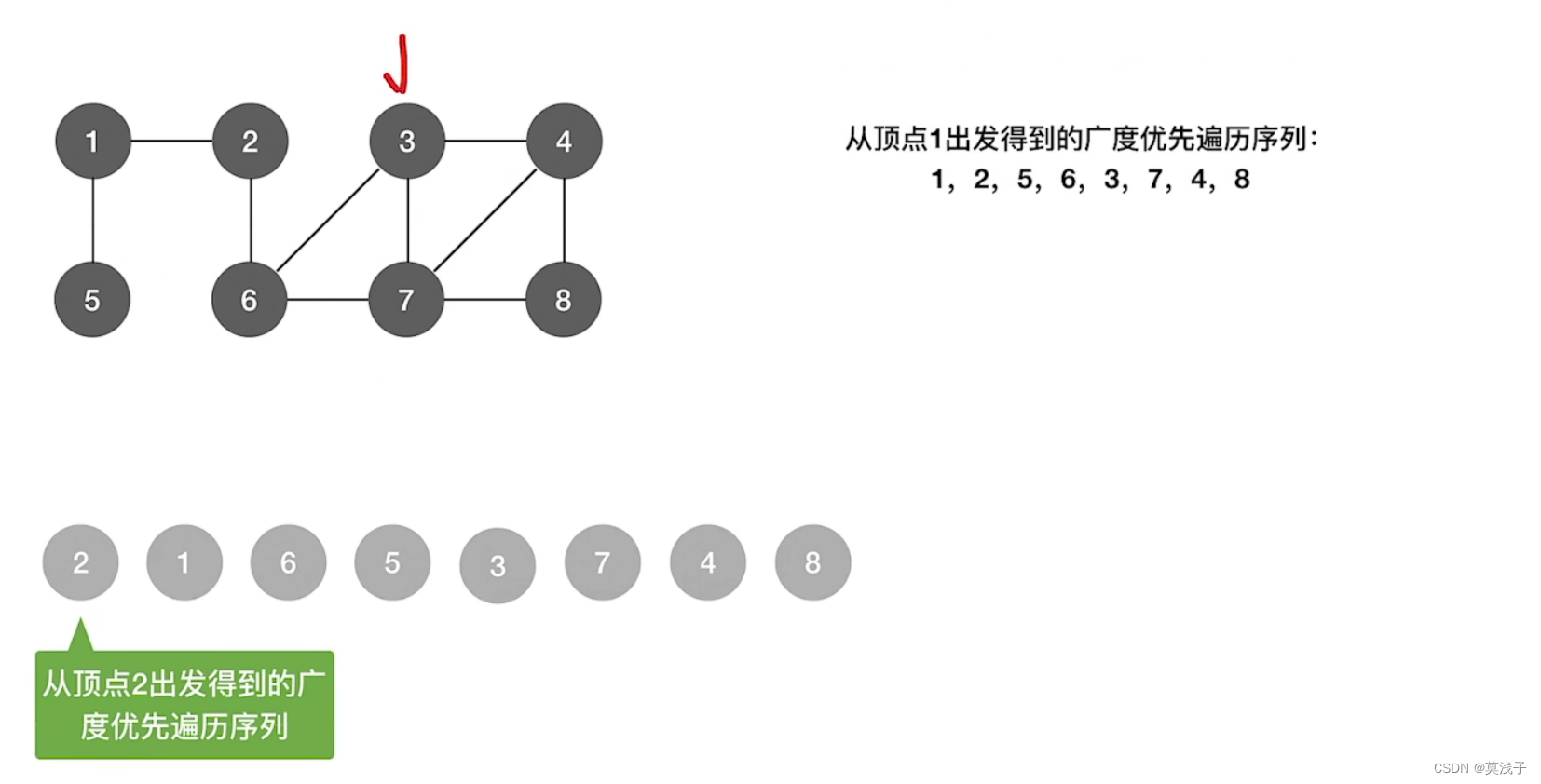
按照上面的例子，首先
我们先遍历到 2 ，2 放到队列，如果队列不空，把 1 和 6 放到队尾，然后 1号出队，和 1号邻的为
5和 2 ，由于 2被visit了所以访问未被访问的结点5,5号结点入队，都访问完了，看六号结点，六号结点出队。6号结点相邻的且未被访问的是3 ， 7 。visit 3 和 7 并且都放在队尾，然后看3 ，和3相邻的且未被访问的是4 号，访问4号结点，让4 号结点入队，最后，3号出队，看7号结点，与7号结点相邻的且未被访问的是8号结点。最后所有结点都被访问。
3.算法存在的问题和解决方案
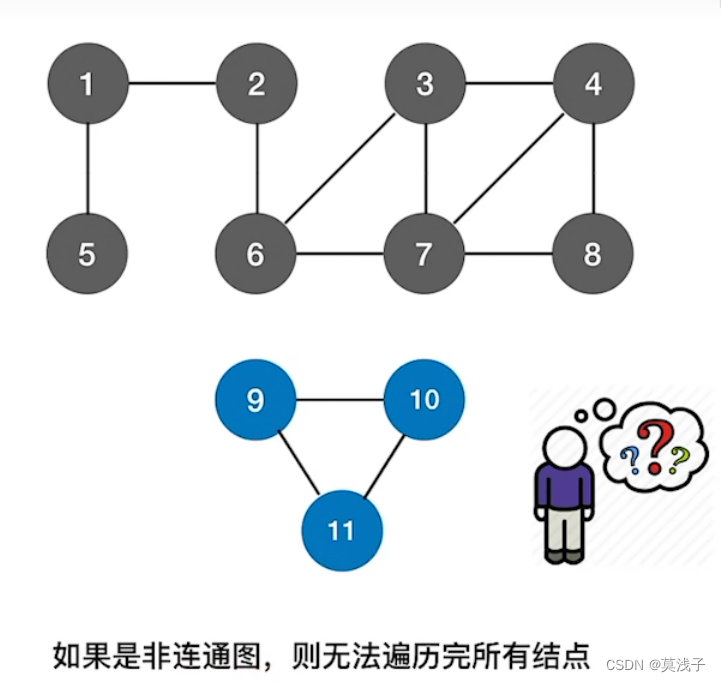
前面介绍的都是连通图，如果是非连通图，那么上面算法就实现不了。我们可以直接从0号结点开始，遍历所有结点查看是否有未被访问的结点，找到第一个值为false的结点。从这个结点出发调用BFS。
代码
bool visited [MAX_VERTEX_NUM] ; //访问标记数组
void BFSTraverse(Graph G){ //对图G进行广度优先遍历
for( i=0; i<G.vexnum;++i)
visited[i]=FALSE; //访问标记数组初始化
InitQueue(Q); //初始化辅助队列Q
for( i=0; i<G.vexnum;++i) //从0号顶点开始遍历
if( !visited[i]) //对每个连通分量调用一次BFS
BFS(G,i); // vi未访问过，从vi开始BFS
}
bool visited [MAX_VERTEX_NUM];/访问标记数组
//广度优先遍历
void BFS( Graph G,int v){//从顶点v出发，广度优先遍历图G
visit(v); //访问初始顶点v
visited [v]=TRUE; //对v做已访问标记
Enqueue(Q,v); //顶点v入队列Q
while( !isEmpty(Q) ){
DeQueue(Q, v); //顶点v出队列
for(w=FirstNeighbor(G,v ) ;w>= ; w=NextNeighbor(G,v,w))
//检测v所有邻接点
if( !visited [w] )//w为v的尚未访问的邻接顶点
{
visit(w);//访问顶点w
visited [w]=TRUE;//对w做已访问标记
EnQueue(Q,w);//顶点w入队列
}
}
4.知识回顾与总结
图的深度优先遍历
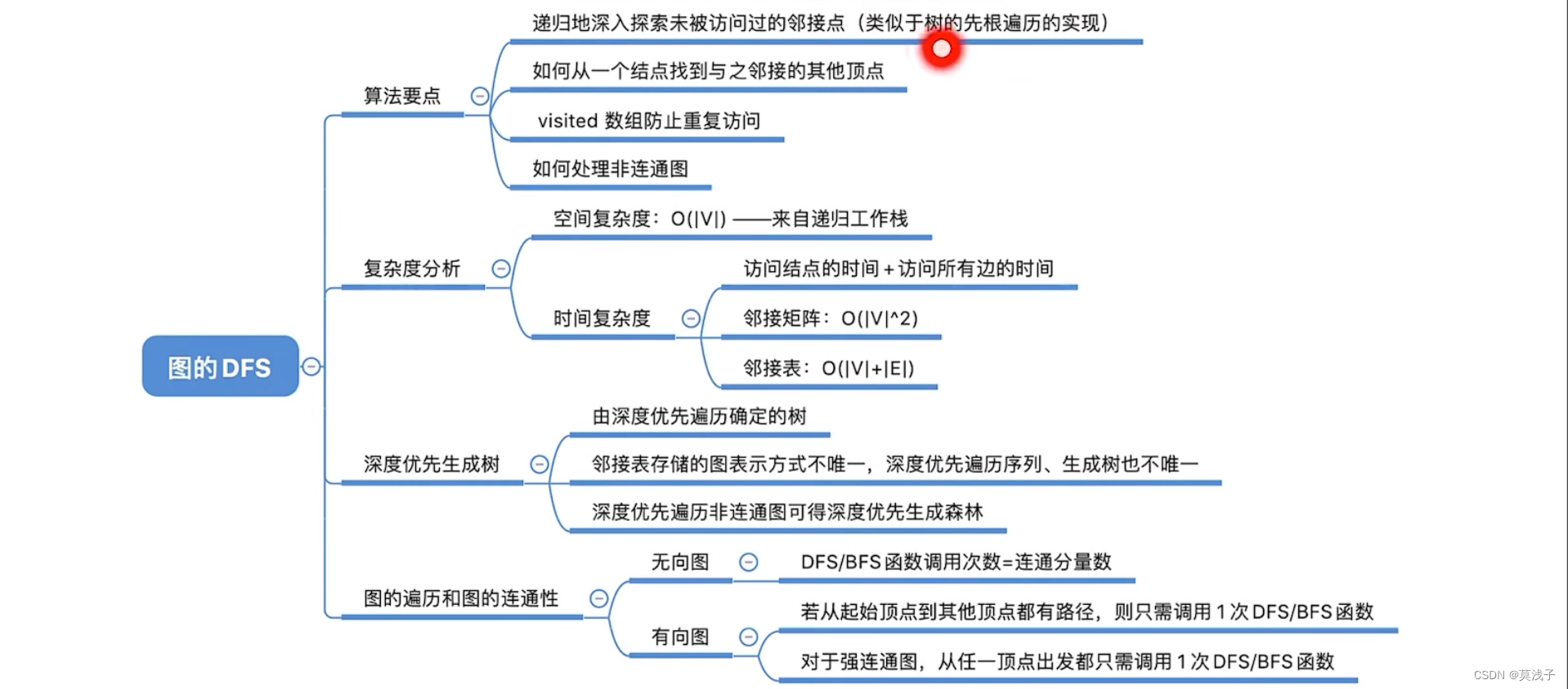
1.树的深度优先遍历
树的深度优先遍历有点类似于先根遍历
首先遍历 1 2 5 6 3 4 7 8 ，它的遍历更趋向于先深层的遍历树。
2.图的深度优先遍历
首先我们可以先看一下2，和2相邻的是1号结点和6号结点。和2相邻的第一个结点是1，所以先访问1，1号结点未被访问。和1号结点相邻的为2 号和5号，但是2号被访问过了，所以看5号结点。和5号结点相邻的结点点都被访问过。这个顶点的DFS调用完，返回到1号接点调用层，但是1号节点调用都被调用完了，那么就可以返回2号结点调用层，2号结点身边的结点未被访问。即是6号结点。和6号结点相近的且未被访问的是 3和 7号结点，先访问3号结点，下一个应该被访问的是4号结点，和4号相邻的且未被访问的是7号结点，最后8号结点未被访问，访问一下8号结点。
代码
bool visited [MAX_VERTEX_NUM] ;//访问标记数组
void DFS(Graph G,int v){ //从顶点v出发，深度优先遍历图G
visit(v ); //访问顶点v
visited [v]=TRUE; //设已访问标记
for( w=FirstNeighbor(G,v) ;w>=0 ; w=NextNeighor(G,v,w) )
if( !visited [w] ){ //w为u的尚未访问的邻接顶点
DFS(G,w) ;
}
3.算法存在的问题和解决方案
与广度优先算法一样，如果存在非连通图，那么同样的，我们可以直接从0号结点开始，遍历所有结点查看是否有未被访问的结点，找到第一个值为false的结点。从这个结点出发调用BFS。
最终代码
bool visited [MAX_VERTEX_NUM];//访问标记数组
void DFSTraverse(Graph G){ //对图G进行深度优先遍历
for( v=0; v<G.vexnum;++v)
visited[v]=FALSE; //初始化已访问标记数据
for( v=0 ; v<G.vexnum; ++v) //本代码中是从v=0开始遍历
if( !visited[v])
DFS(G,v);
}
bool visited [MAX_VERTEX_NUM] ;//访问标记数组
void DFS(Graph G,int v){ //从顶点v出发，深度优先遍历图G
visit(v ); //访问顶点v
visited [v]=TRUE; //设已访问标记
for( w=FirstNeighbor(G,v) ;w>=0 ; w=NextNeighor(G,v,w) )
if( !visited [w] ){ //w为u的尚未访问的邻接顶点
DFS(G,w) ;
}
4.知识回顾与总结
- 点赞
- 收藏
- 关注作者
评论（0）