MEASUREMENT MODELS AND PRINCIPLES FOR TOA SOURCE LOCALIZATION

The TOA, TDOA, RSS, and DOA signal models and their basic positioning principles are presented in Sections 2.2.1 – 2.2.4 , respectively. In fact, all the models can be generalized as

where r is the measurement vector, x is the source position to be determined, f ( x ) is a known nonlinear function in x , and n is an additive zero - mean noise vector.

TOA

TOA is the one - way propagation time of the signal traveling between a source and a receiver. This implies that the target and all receivers are required to be precisely synchronized to obtain the TOA information, although such synchronization is not needed if the round - trip or two - way TOA is measured. Multiplying the TOAs by the known propagation speed, denoted by c , provides the distances between the source and receivers. For example, c ≈ 340 m/s and c ≈ 3 * 10 ^8 m/s are the speeds of sound and light, respectively, in the in - air scenarios. In the absence of measurement error, each TOA corresponds to a circle centered at a receiver on which the source must lie in the 2 - D space. As discussed in Chapter 1 , geometrically, three or more circles deduced from the noise - free TOAs will result in a unique intersection, which is the source position, implying that at least three sensors are needed for 2 - D positioning.

Note that two TOA circles generally have two intersection points, which correspond to two possible source locations. Nevertheless, these circles may not intersect or have multiple intersections in the presence of disturbance, and hence it is not an effective way to solve the problem using the circles directly. In fact, with three or more receivers, it is more appropriate to convert the noisy TOAs into a set of circular equations from which the source position can be determined according to an optimization criterion, with the knowledge of the sensor array geometry.

Mathematically, the TOA measurement model is formulated as follows. Let be the unknown source position and be the known coordinates of the l th sensor, l = 1, 2, … , L , where L ≥ 3 is the number of receivers. The distance between the source and the l th sensor, denoted by , is simply

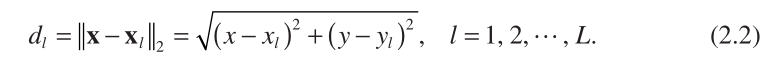
Without loss of generality, we assume that the source emits a signal at time 0 and the l th sensor receives it at time  ; that is, { } are the TOAs and we have a simple relationship between  and

In practice, TOAs are subject to measurement errors. As a result, the range measurement based on multiplying  by c, denoted by  is modeled as

实际上，TOA会受到测量误差的影响。 结果，基于  乘以 c 的范围测量 表示为  它被建模为

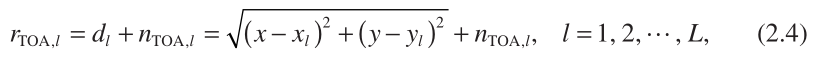
where  is the range error in  , which results from the TOA disturbance.

Equation 2.4 can also be expressed in vector form as

Here,   represents the known function, which is parameterized by x , and in fact, it is the noise - free distance vector. The source localization problem based on TOA measurements is to estimate x given { } or .

To facilitate the algorithm development and analysis as well as the CRLB computation, it is assumed that {  } are zero - mean uncorrelated Gaussian processes with variances . It is noteworthy that the zero - mean property indicates LOS transmission. The probability density function ( PDF ) for each scalar random variable , denoted by , has the form of

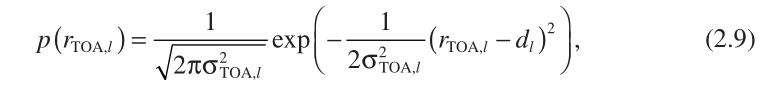
为了便于算法开发和分析以及CRLB(Cramer-Rao Lower Bound)计算，假设{  } 为零均值不相关的高斯过程，方差为 . 值得注意的是，零均值属性表明LOS（line-of-sight）传输。每一个随机变量  的概率密度函数为式（2.9）.

文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。

原文链接：reborn.blog.csdn.net/article/details/83660507