前言

复习acwing算法基础课的内容，本篇为讲解数学知识：拓扑排序，关于时间复杂度：目前博主不太会计算，先鸽了，日后一定补上。

一、拓扑排序

需要注意只有有向图才有拓扑序列
有向无环图一定存在拓扑序列，有向无环图也被称为拓扑图
这里再来介绍两个概念：
入度：这个点由几个点可直接到达
出度：这个点由几条出边

这里举一个例子来说明这两个概念，比如对于下图：

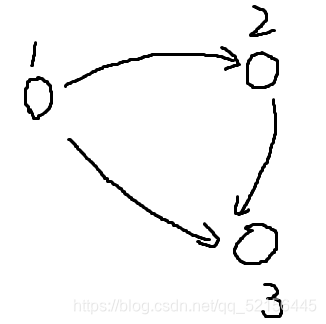
    入度    出度
1    0       2
2    1       1
3    2       0

注意：一个有向无环图一定至少存在一个入度为0的点

二、AcWing 848. 有向图的拓扑序列

本题链接：AcWing 848. 有向图的拓扑序列
本博客提供本题截图：

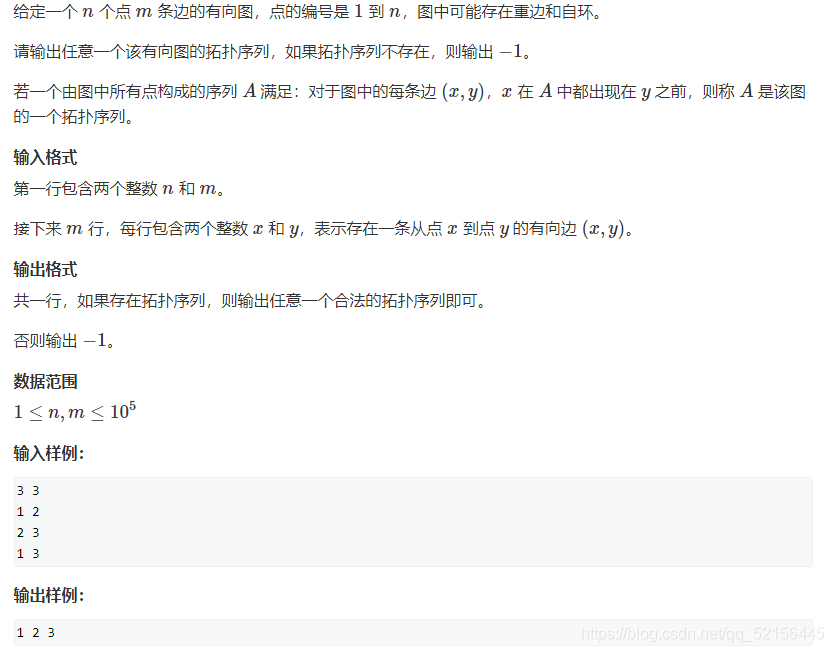
本题解析

数组d存储的是每一个点的入度，本题用到了用数组模拟队列，链表，BFS的相关知识，对于这些知识，本博客不做解释.
我们首先把所有入度为0的点都加入到我们的队列中，入度为0的点代表的就是起点，对于每次操作都是取出队头t，然后枚举t的所有出边，注意取出队头t的时候，我们需要把t能到达的所有出边对应的入度减1，如果减1之后这个点的入度为0的话，就把它加入到队列之中，最后我们队列中的存储的就是整个拓扑序列.

AC代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int h[N], e[N], ne[N], idx;
int d[N];
int q[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool topsort()
{
    int hh = 0, tt = -1;

    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (-- d[j] == 0)
                q[ ++ tt] = j;
        }
    }

    return tt == n - 1;
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);

        d[b] ++ ;
    }

    if (!topsort()) puts("-1");
    else
    {
        for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);
        puts("");
    }

    return 0;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
 

三、时间复杂度

关于拓扑排序时间复杂度以及证明，后续会给出详细的说明以及证明过程，目前先鸽了。

文章来源: chen-ac.blog.csdn.net，作者：辰chen，版权归原作者所有，如需转载，请联系作者。

原文链接：chen-ac.blog.csdn.net/article/details/117954828