AOV网(Activity On Vertices)

• 在一个表示工程的有向图中，用顶点表示活动，用有向边<Vi, Vj>表示活动Vi 必须先于活动Vj 进行。这种有向图叫做顶点表示活动的AOV网络 。

AOV网特点：

• AOV网中的弧表示活动之间存在的某种制约关系
• AOV网中不能出现回路

算法思想

• 输入AOV网络。令 n 为顶点个数。
• 在AOV网络中选一个没有直接前驱的顶点, 并输出之;
• 从图中删去该顶点, 同时删去所有它发出的有向边;
• 重复以上 2、3 步, 直到：
  • 全部顶点均已输出，拓扑有序序列形成，拓扑排序完成；或：
  • 图中还有未输出的顶点，但已跳出处理循环。这说明图中还剩下一些顶点，它们都有直接前驱，再也找不到没有前驱的顶点了。这时AOV网络中必定存在有向环。

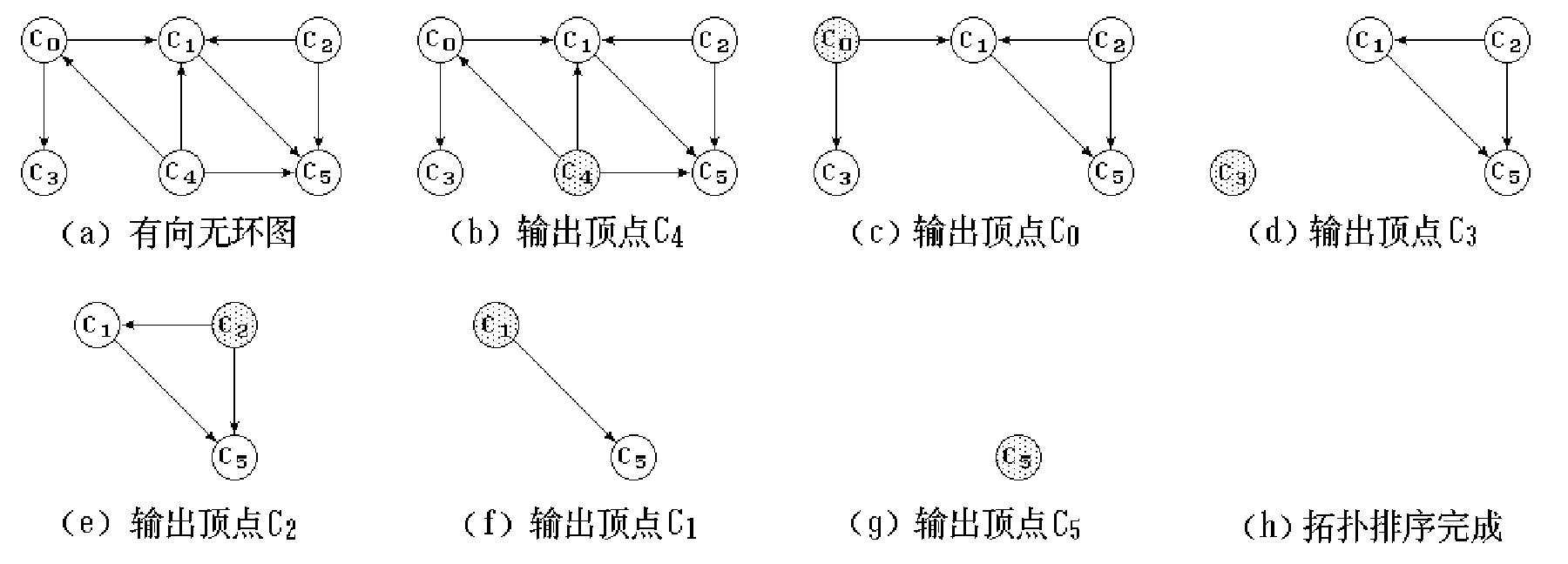
算法实现

为避免每次都要搜索入度为零的顶点，在算法中设置一个**“栈”**，以保存“入度为零”的顶点。

void FindInDegree(ALGraph G, int indegree[]){
	// 求各顶点的入度
	for(i = 0; i < G.vexnum; i++)
		indegree[i] = 0;
	for(i = 0; i <G.vexnum; ++i){
		p = G.vertices[i].firstarc;
		while(p != NULL){ indegree[p->adjvex]++; p = p->nextarc;
		}
	}
}

void TopologicalSort(ALGraph G){
	// 拓扑排序
	FindInDegree(G, indegree);  // 对各顶点求入度
	InitStack(S);
	for(i = 0; i < G.vexnum; i++)
		if(!indegree[i]) Push(S, i);  // 入度为零的顶点入栈
	count = 0;  // 对输出顶点计数
	while(!EmptyStack(S)){
		Pop(S, i);
		++count;
		cout << G.vertices[i].data;
		for(p = G.vertices[i].firstarc; p; p = p->nextarc){ k = p->adjvex; --indegree(k);  // 弧头顶点的入度减一 if(!indegree[k]) Push(S, k);  // 新产生的入度为零的顶点入栈
		}
	}
	if(count < G.vexnum)
		cout << "图中有回路";
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
 

文章来源: ruochen.blog.csdn.net，作者：若尘，版权归原作者所有，如需转载，请联系作者。

原文链接：ruochen.blog.csdn.net/article/details/103977070