1、机器学习背后的微分入门
为了理解更深层次的原理,让我们再来讨论一下最简单的神经网络——感知器(perceptron)。感知器是由Frank Rosenblatt在1957年发明的,要想理解它,请参考图1。

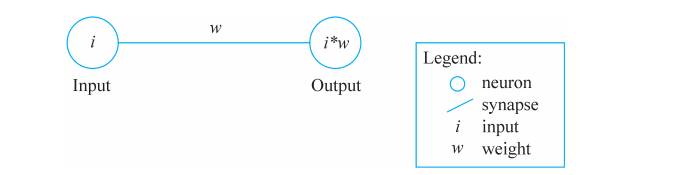
■ 图1 感知器概念表示
图1中有两个圆,一个在左边,另一个在右边,有一条线连接着这两个圆。如果你把它映射到生物学术语上,可以将圆看作神经元(neurons),而这条线将是一个突触(synapse)。这条线有一个叫作权重(weight)的值,它描述了两个神经元之间连线的重要程度。
简言之,神经元是一种特殊的细胞,是人类神经系统中可以携带信号的一个基本单元。突触是两个神经元之间的连接。
左边的神经元称为输入神经元。你不需要计算它的值,而是为它提供一个值,假设我们给了它一个0.2的值。右边的神经元称为输出神经元,它的值取决于与它相连的神经元的值。在本例中,只有一个神经元连接到输出神经元,输出神经元的值是输入神经元的值和突触的值的乘积。
换言之,你将每个输入神经元乘以其各自的权重,并将这些乘积相加在一起,就可以得到输出神经元的值。假设权重的值为0.4,现在让我们根据输入i和权重w计算输出神经元o的值:

就是这样!现在让我们代入值并查看结果:

现在我们得到了一个输出值。但是一个神经网络并没有这么简单,除非你可以训练它提供你想要的输出。在本例中,假设我们希望神经网络做一个简单的任务: 对提供的输入取负。所以,在这个例子中,我们想得到输出-0.2,但我们却得到了0.08。
下表给出了变量最初的简化视图。

为了获得更好的输出,我们需要改变权重的值,以更接近预期的结果。那么我们该怎么做呢?我们需要用到一些微分的知识。别担心,你不需要知道任何高级的微分知识。
在我们弄清楚新的权重应该是什么之前,我们需要首先看看神经网络距离预期输出有多少偏差,这被称为损失函数或误差函数。在本例中,我们取期望输出和神经网络输出之间的平方差,假设预期输出z为

让我们来计算一下损失:

这就是说,神经网络的“不正确性”是0.0784。但这是如何帮助我们计算新权重的呢?答案是通过计算损失函数的导数,我们有了一个新的函数,它可以告诉我们如何更新权重以更接近期望的输出。你不需要担心该函数是如何工作的,你只需要知道

这就是说,神经网络的“不正确性”是0.0784。但这是如何帮助我们计算新权重的呢?答案是通过计算损失函数的导数,我们有了一个新的函数,它可以告诉我们如何更新权重以更接近期望的输出。你不需要担心该函数是如何工作的,你只需要知道

是损失函数对权重的导数,我们继续来计算一下。

计算结果如下:

现在我们得到了损失函数的导数值。我们应该如何使用它更新权重呢?
在这里,你需要明白一些事情: 你不能只更新权重,你必须通过一定的量调整权重,这被称为学习率(learning rate)。就像人类一样,如果学习率太高(一个学得太快的人),神经网络根本就不会学到很多内容;如果学习率太低,神经网络则需要太长时间进行学习。所以你需要一个很合适的学习率。在本例中,我们使用0.1的学习率:

计算结果如下:
好吧!让我们尝试用神经网络进行预测:

哇,我们比之前更接近期望输出了。我们想要的输出是-0.2,但我们得到的输出是0.08,我们的输出值0.08距离-0.2为0.28。然而,在我们通过微分运算进行处理后,我们得到的输出为0.07776。现在,这个新输出0.07776距离-0.2是0.27776。
下表给出了一次迭代后系统如何学得比以前更好的简化视图。

从另一个角度来看,让我们再次计算损失:

我们从0.078降到了0.077。现在,如果我们继续重复这个过程,我们应该会得到一个可接受的值。对于更大的数据集,我们可能需要重复成千上万次才能获得较好的结果。
此外,你只是根据一个训练样本计算了一个新的权重值。数据并不是很多,神经网络需要更多的数据进行学习。如果你想用更多的样本进行训练,那么一种方法就是对多个训练样本的损失进行平均。

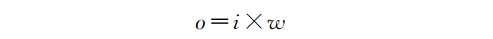
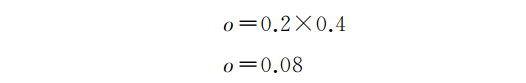

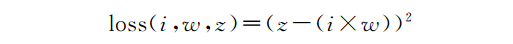
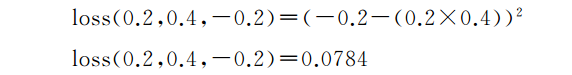
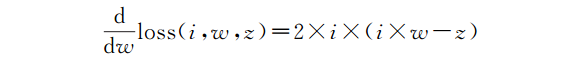
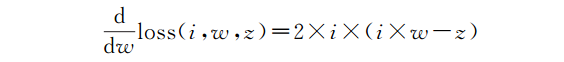
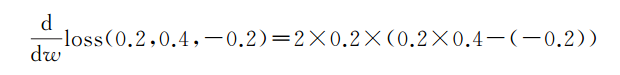
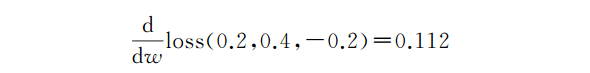
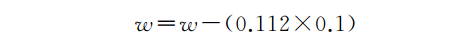
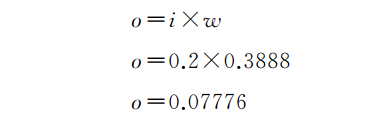

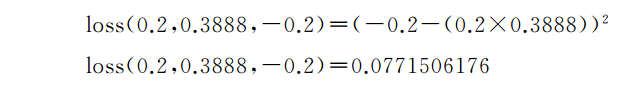

评论(0)