致谢

本文参考资料如下

拉普拉斯平滑（Laplacian smoothing）_潜心学习的渣渣的博客-CSDN博客_拉普拉斯平滑

极大似然估计详解_知行流浪-CSDN博客_极大似然估计

极大似然估计原理详细说明_majunfu-CSDN博客_极大似然估计的原理

(1条消息) 多项式分布的理解概率公式的理解_猪逻辑公园-CSDN博客_多项式分布

常用的概率分布:伯努利分布、二项式分布、多项式分布、先验概率，后验概率 - 志光 - 博客园 (cnblogs.com)

十分钟学习 统计学习方法 李航 第二版 之《4.1 朴素贝叶斯法：核心——贝叶斯定理》_哔哩哔哩_bilibili

【AI 版】十分钟学习 统计学习方法 李航 第二版 之《4.4 朴素贝叶斯法：极大似然法之原理篇》_哔哩哔哩_bilibili

6 朴素贝叶斯

6.1 概述

这一讲我们要学习的是朴素贝叶斯算法。其属于有监督学习。

贝叶斯分类是一种分类算法的总称，这种算法均以贝叶斯定理为基础，故统称为贝叶斯分类。

贝叶斯分类器的主要特点有：

• 属性可以离散，也可以稳定。
• 数学基础扎实，分类效率稳定。
• 对缺失和噪声数据不太敏感。
• 属性如果不相关，分类效果很好，如果相关，则不低于决策树

让我们来直观对比一下KNN和朴素贝叶斯吧。在KNN中，我们通过模型来预测的结果一般可以通过和某类别的点距离远近给出该样本的所在分类；而对于决策树，其一般是算出该样本在各个类别中的概率，在哪个类别概率大就属于哪个类别。

现在假如我们引出一个事件。

有一天我们坐在办公室里，看到有人快速的走过，我们没有看到这个人是谁。但是我们做一个猜测，Alex和Brenda坐在办公室的时间一样长，那么这两人都各有百分之五十的概率是那个快速走过的人。

那现在我们又有一条新的推断信息，两个人都有一件红色的毛衣，而那个快速走过的人身上就穿了一件红色的毛衣。对于Alex来说她一个星期穿两次，而Brenda一个星期穿三次，所以这样的话快速走过的人是Alex的概率变成了百分之四十，是Brenda的概率变成了百分之六十。

在这里，在我们还没有新信息时，我们得到的百分之五十是先验概率。然后我们有了新信息后，我们得到了百分之四十和百分之六十。最后猜测的这两个概率被称为后验概率。

现在还是刚才那个例子，加入我们还是看到一个人飞跑过去，跑的太快我们没注意，然后靠推断看看这个人是谁。我们最开始知道的消息是，Alex一个星期中有三天是待在办公室的，而Brenda一个星期只有一天是待在办公室的。所以Alex的先验概率是0.75，而Brenda是0.25，然后我们假设连续好几周都是这种情况，那么我们可以很简单的列一个表格。

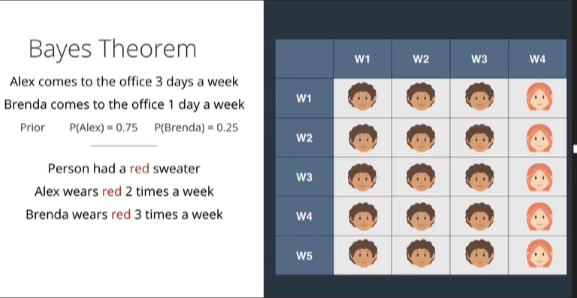
那么现在很先前一样，Alex每周有两次穿红色毛衣，而Brenda每周有三次穿红色毛衣。那么穿毛衣总数我们把他在表格中标红，两人穿红色毛衣的次数共九次。

因此，如果我们看到一个穿着红色毛衣的人快速经过，这个人是Alex的概率（后验概率）是三分之二，是Brenda的概率（后验概率）是三分之一。那么穿毛衣总数我们把他在表格中标红，两人穿红色毛衣的次数共九次。

因此，如果我们看到一个穿着红色毛衣的人快速经过，这个人是Alex的概率（后验概率）是三分之二，是Brenda的概率（后验概率）是三分之一。

总的来说就是：先验概率为主观判断的概率，某种新信息改变我们的主观判断后，得出的最终结论我们叫做后验概率。

让我们用下面的数学方式来算一次：

我们开始的时候，Alex一个星期在办公室三次，Brenda一个星期在办公室一次，那么就是四分之三和四分之一的概率，而后，两人穿红毛衣的概率和不穿红毛衣概率分别是0.4和0.6，0.6和0.4。然后分别计算他们的条件概率，如下图所示。

然而，我们要的仅仅是找出那个人，找不出的因素和我们没什么关系，所以我们把其他因素舍去，然后使主要因素的总数之和为一。

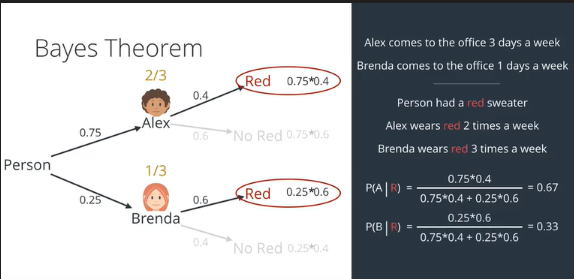
由上图我们可以把步骤一般化，那么可得贝叶斯公式如下。

现在我们换一个更好的例子来理解贝叶斯公式。

假如你身体不舒服，要去医院看医生，医生告诉你，你可能的了某种严重的疾病，而且诊断这种疾病的准确率是百分之99。（先验概率）然后你在等待检测的过程中，上网搜索了一下资料，然后发现平均有万分之一的人患这种病。结果你在检测完的第二天医生就打电话来告诉你，你的检查结果为阳性，这时候你感到开始恐慌了，那请问我们患病的概率是多少？

我们用数学的方法好好来计算一下，假设现在有一百万人，那么就有999900人健康，100人患病，健康的人中，可能有9999的人会被误诊，有989901个人检测正确，而患病的人里面有99个成功检测并得到治疗，有一个人是诊断不出来而乖乖送死。

那么按我们刚才的计算，我们应该计算出来的患病概率为：0.0098

6.2 概率论

6.2.1 大数定律

我们来对上面的知识做一个归档。假如现在我们有一枚硬币，我们定义一个概率事件：扔出一个硬币，结果头像朝上的可能性为几。

如果在这个硬币质地均匀的情况下，我们会不加思索地回答：百分之50。实际上，这个浅显易懂的道理是根据大数定律推断出来的。大数定律的内容是：如果统计数据足够大，那么事件出现的概率就能无限接近它的期望值。

6.2.2 基本概念

• 事件：每种结果

• 样本空间（结果空间）：所有基本事件的集合Ω，例如投掷一次硬币的样本空间是：{正,反}；投掷一次骰子的样本空间是：{1,2,3,4,5,6}

• 样本点：样本空间元素（基本事件w）

• 联合概率：联合概率也是我们说的and事件，即A = a和B = b同时发生的概率是多少。

• 条件概率：设AB两个事件，且P(B)>0，则称$\frac{P(AB)}{P(B)}$为事件B已发生的条件下事件A发生的条件概率记为P(A|B)。

• 独立性：我们常说的独立性说成大白话就是互不影响，比如连续抛出两次骰子，第二次抛出不会受第一次影响；还有投篮啊，打靶啊都是独立的；也就是说，设有A、B是两个任意事件，如果P(AB) = P(A)P(B)，则称事件A和B相互独立，简称A和B独立。

• 乘法定理：P(A|B) = $\frac{P(AB)}{P(B)}$

• 贝叶斯定理：贝叶斯定理也叫逆概公式。由于P(AB)可以以乘法定理为桥梁，拓展出$P(AB)=P(B|A)P(A)或者P(AB)=P(A|B)P(B)$ , 所以当以P(AB)为桥梁时，贝叶斯定理就产生了

  $P(A|B)=\frac{P(B|A)P(A)}{P(B)}$

6.2.3 极大似然估计

为了下面的学习更加顺畅，我们有必要讲述一下概率论中的极大似然估计（最大似然估计）。

最大似然估计原理的思想可以用一个例子来说明。假设由两个外形完全相同的箱子，甲箱有99只白球，1只黑球；乙箱有99只黑球，一只白球。假设现在有个人摸到一颗球拿到你的面前，你大概率认为它是从乙箱拿出来的。

这里我们讲的“大概率”，被人们称为最大似然原理。

如果从前面的叙述来看，我们用标准的叙述来表述上面的知识点，最大似然估计在做一件事是：利用已知的样本结果，反推最有可能导致这个结果的参数值。在概率论中，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即模型已定，参数位置。通过若干次实验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为最大似然估计。

6.2.4 多项式分布

多项式分布式二项分布的推广。在这之前，我们先了解一些其他的概念。

6.2.4.1 伯努利分布

伯努利分布又叫0-1分布，指一次随机试验，结果只有两种。这种分布典型的是投一次硬币，预测结果是正是反。

6.2.4.2 二项分布

二项分布为n次伯努利实验的结果。如果我们扔n次硬币，p为硬币朝上的概率，那么扔第k次硬币朝上的概率如下所示：
$$P(X=k)=C_n^k{p}^k(1-p{)}^{n-k},k=0,1,2,3,4,...n$$

6.2.5 朴素贝叶斯

下面我们来举个朴素贝叶斯最热门的应用——垃圾邮件过滤器。我们手机上或多或少都收到垃圾邮件过，每个垃圾邮件上面写的是什么：赢钱很容易之类的词，而正常邮件上面写的是什么：你好，你过的怎么样之类的词。而我们要做的，就是拿到一封邮件时，赢钱这类词属于垃圾邮件的概率是多少。如下图：

这里我们根据上面可以看出，垃圾邮件含有容易这个词的概率是三分之一，含有钱这个词的概率是三分之二。我们现在就是根据贝叶斯公式算出含有容易这个词的垃圾邮件出现的概率是二分之一，含有钱这个词垃圾邮件出现的概率是三分之二。

而朴素贝叶斯的“朴素”此时就要体现在这里了。

我们假设“容易”和“钱”是相互独立互不影响的两个词，那么我们可以利用事件的独立性对两个概率相乘。那么我们得出来的概率即为：如果同时含有“容易”和“钱”的两个词，那么这个邮件是垃圾邮件的概率是多少三分之一。

当然，这种想法肯定在数学上是不合逻辑的，但是这样的假设通常能帮我们得到理想的结果，毕竟他还是有一定道理的。即使这种假设是天真、不成立的假设，但是在实践中效果很好，使算法效率变高。

总结一句话就是：朴素贝叶斯实际上等于朴素+贝叶斯，其中朴素是指特征相互独立，而贝叶斯是指贝叶斯公式。朴素贝叶斯常用于文本分类。

6.3 朴素贝叶斯文本分类

6.3.1 一个例子

我们把上述的贝叶斯公式应用于文本分类中，则公式可变为：
$$P(C|F_1,F_2,...)=\frac{P(F_1,F_2,...|C)P(C)}{P(F_1,F_2,...)}$$
其中公式可以分为三个部分：

• P©：每个文档类别的概率（某文档的类别数/总文档数量）
• P(W|C)：给定类别下特征的概率（被预测文档中出现的词）。
  • 计算方法：$P(F_1)=N_i/N(训练文档中去计算)$，其中$Ni$为该$F_1$词在C类别所有文档中出现的次数，N为所属类别C下的文档所有词出现的次数和。
• P(F_1,F_2，…)：预测文档中每个词的概率

可能以上的公式绕的你眼花缭乱，我们结合例子来看一下。

在下面的例子中我们要做的是这么一件事，在某些特别的分类文档如China类中，它们时常会出现训练集中的词，如Chinese Beijing、Chinese等。但是出现这类词不一定就是China类。而我们要做的，就是在测试集中给出一篇新文章，根据文章中的词来判断该文章属不属于China类。

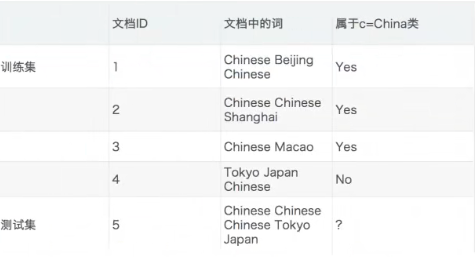
让我们用贝叶斯公式来计算一下，我们实际上是要计算测试集中该文档的$P = (C|Chinese,Chinese,Chinese,Tokyo,Japan) 和 P(非C|Chinese,Chinese,Chinese,Tokyo,Japan) $，然后比对其大小即可判断该文档是否属于该类别。我们看一下下面的计算过程，如果不是没有笔的情况，我建议你也算一下。

可以看出，最后算出来$P(F|C)$的概率为0，也就意味着带入贝叶斯公式，$P(C|F)$的概率也为0，这怎么可能！从测试集中文档含有三个Chinese来看，这篇文档再怎么不济也不可能属于Chinese的概率是0。而之所以概率为0，究其原因是因为样本量太少，没有出现Tokyo和Japan。为了防止这种概率为0的情况发生，我们引入下面的知识点。

6.3.2 拉普拉斯平滑系数

拉普拉斯平滑系数是法国数学家拉普拉斯首先提出来的，是为了解决零概率问题的发生。其基本思想是假定训练样本很大，每个分量x的计数加1造成的估计概率变化可以忽略不计，但是这种操作却可以有效地避免零概率问题。

对于上述6.3.1的文本分类问题，我们可以把拉普拉斯平滑系数改写为如下形式：
$$\begin{gathered} P(F1|C)=\frac{N_i+a}{N+am} \\ 其中a为指定的系数，一般为1 \\ m为训练文档中统计出的特征词个数 \end{gathered}$$
结果拉普拉斯平滑系数这把利剑，让我们再次计算上面的$P(F|C)$。

6.3.3 算法实现

我们要做一个案例来加强我们前面的学习，我们要利用多项式贝叶斯分类器来对新闻组数据集进行分类。分类的步骤如下：

• 获取数据
• 划分数据集
• 特征工程
• 朴素贝叶斯估计器流程
• 模型评估

在sklearn中朴素贝叶斯的API为：

sklearn.naive_bayes.MultinomialNB(alpha = 1.0，fit_prior = True, class_prior = None)

• 其中alpha为拉普拉斯平滑系数，浮点数类型

新闻数据集的来源为：

20个新闻组数据集是大约20000个新闻组文档的集合，平均分布在20个不同的新闻组中。它最初是由Ken lang手机的。

数据被组织成20个不同的新闻组，每个新闻组对应不同的主题。

# 导入模块
from sklearn.datasets import fetch_20newsgroups
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer


def nb_news():
    """导入数据并且处理"""
    # 获取数据
    news = fetch_20newsgroups(subset="all")

    # 2 划分数据集
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, random_state=6)

    # 3 文本特征抽取
    transfer = TfidfVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4 朴素贝叶斯算法预估器流程
    estimator = MultinomialNB()
    estimator.fit(x_train, y_train)

    # 5 模型评估
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对预测值和真实值：\n", y_test == y_predict)

    # 计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

    return None


nb_news()

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
 

6.4 贝叶斯分类器

虽然掌握一个贝叶斯分类器已经很艰难了，但请允许我让你更难受。在下面，我们讲述其余种类的贝叶斯分类器。我们将使用手写数据集为例子进行分类。

6.4.1 多项式贝叶斯分类器

实际上，我们前面用到的贝叶斯分类器是多项式贝叶斯分类器，让我们仔细看一下它。

sklearn.naive_bayes.MultinomialNB(alpha = 1.0，fit_prior = True, class_prior = None)

• 其中alpha为拉普拉斯平滑系数，浮点数类型
• 多项式贝叶斯分类器实际上假设特征的条件概率符合多项式分布

6.4.2 高斯贝叶斯分类器

sklearn.naive_bayes.GaussianNB

• 该分类器没有参数
• 该分类器假设特征的条件概率分布满足高斯分布

6.4.3 伯努利贝叶斯分类器

sklearn.naive_bayes.BernoulliNB(alpha = 1.0,binarize = 0.0,fit_prior = True,class_prior = None)

• alpha：拉普拉斯平滑系数
• binarize：一个浮点数或者None，如果是None则假定原始数据已经二元化，如果是浮点数则以该数为界，特征取值大于它的作为1，特征取值小于它的作为0
• fit_prior：布尔值。如果为True，则不去学习P($y=c_k$)，替代以均匀分布；如果为false，择取学习P($y=c_k$)
• class_prior：一个数组。它指定了每个分类的先验概率。如果指定了该参数，则每个分类的先验概率不再从数据集中学得

6.4.4 代码实现

# 导入模块
from sklearn import datasets, naive_bayes
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt


def show_digits():
    """查看手写数据集内容"""
    digits = datasets.load_digits()
    # 构建画布
    fig = plt.figure()
    # 输出
    print("vector from image 0:", digits.data[0])
    for i in range(25):
        ax = fig.add_subplot(5, 5, i + 1)
        ax.imshow(digits.images[i], cmap=plt.cm.gray_r, interpolation='nearest')
        plt.show()


def load_data():
    """加载数据集"""
    digits = datasets.load_digits()
    return train_test_split(digits.data, digits.target, test_size=0.25, random_state=0)


def test_MutinomialNB():
    """调用多项式贝叶斯分类器"""
    digits = datasets.load_digits()
    x_train, x_test, y_train, y_test = load_data()
    # 设置转换器
    estimator = naive_bayes.MultinomialNB()
    estimator.fit(x_train, y_train)
    # 模型评估
    print("MutinomialNB Train Score:\n", estimator.score(x_train, y_train))
    print("MutinomialNB Test Score:\n", estimator.score(x_test, y_test))


def test_GaussianNB():
    """调用高斯贝叶斯分类器"""
    x_train, x_test, y_train, y_test = load_data()
    # 设置转换器
    estimator = naive_bayes.GaussianNB
    estimator.fit(x_train, y_train)
    # 模型评估
    print("GaussianNB Train Score:\n", estimator.score(x_train, y_train))
    print("GaussianNB Test Score:\n", estimator.score(x_test, y_test))


def test_BernoulliNB():
    """调用伯努利贝叶斯分类器"""
    x_train, x_test, y_train, y_test = load_data()
    # 设置转换器
    estimator = naive_bayes.BernoulliNB
    estimator.fit(x_train, y_train)
    # 模型评估
    print("BernoulliNB Train Score:\n", estimator.score(x_train, y_train))
    print("BernoulliNB Test Score:\n", estimator.score(x_test, y_test))


# 调用函数
# test_MutinomialNB()
# test_GaussianNB()
test_BernoulliNB()

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
 

文章来源: blog.csdn.net，作者：ArimaMisaki，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/chengyuhaomei520/article/details/123370921