• [Python从零到壹] 十.Selenium爬取在线百科知识万字详解（NLP语料构造必备技能）

• [Python从零到壹] 十三.机器学习之聚类分析万字总结全网首发（K-Means、BIRCH、层次聚类、树状聚类）
• [Python从零到壹] 十四.机器学习之分类算法五万字总结全网首发（决策树、KNN、SVM、分类对比实验） 
• [Python从零到壹] 十五.文本挖掘之数据预处理、Jieba工具和文本聚类万字详解
• [Python从零到壹] 十六.文本挖掘之词云热点与LDA主题分布分析万字详解
• [Python从零到壹] 十七.可视化分析之Matplotlib、Pandas、Echarts入门万字详解
• [Python从零到壹] 十八.可视化分析之Basemap地图包入门详解

一.图像几何变换

图像几何变换不改变图像的像素值，在图像平面上进行像素变换。适当的几何变换可以最大程度地消除由于成像角度、透视关系乃至镜头自身原因所造成的几何失真所产生的负面影响。几何变换常常作为图像处理应用的预处理步骤，是图像归一化的核心工作之一[1]。

一个几何变换需要两部分运算：

• 空间变换：包括平移、缩放、旋转和正平行投影等，需要用它来表示输出图像与输入图像之间的像素映射关系。
• 灰度插值算法：按照这种变换关系进行计算，输出图像的像素可能被映射到输入图像的非整数坐标上[2]。

图像几何变换在变换过程中会建立一种原图像像素与变换后图像像素之间的映射关系，通过这种关系，能够从一方的像素计算出另一方的像素的坐标位置。通常将图像坐标映射到输出的过程称作向前映射，反之，将输出图像映射到输入的过程称作向后映射。向后映射在实践中使用较多，原因是能够避免使用向前映射中出现映射不完全和映射重叠的问题。

图6-1展示了图像放大的示例，右边图中只有(0,0)、(0,2)、(2,0)、(2,2)四个坐标根据映射关系在原图像中找到了相对应的像素，其余的12个坐标没有有效值[3]。

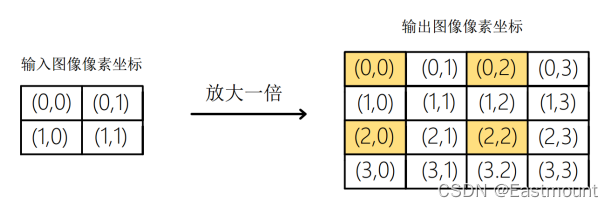
对于数字图像而言，像素的坐标是离散型非负整数，但是在进行变换的过程中有可能产生浮点坐标值。这在图像处理中是一个无效的坐标。为了解决这个问题需要用到插值算法。常见算法如下：

• 最近邻插值
• 双线性插值
• 双立方插值
  图像变换是建立在矩阵运算基础上，通过矩阵运算可以很快找到对应关系。在这篇文章中，我们将介绍常见的图像几何变换，包括图形平移、图像缩放、图像旋转、图像镜像、图像仿射、图像透视等。

二.图像平移

图像平移是将图像中的所有像素点按照给定的平移量进行水平或垂直方向上的移动。假设原始像素的位置坐标为（x0，y0），经过平移量（△x，△y）后，坐标变为（x1, y1），如图6-2所示[3-5]。

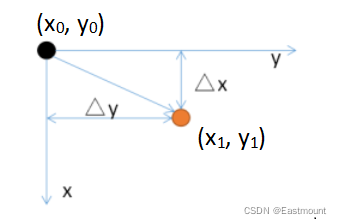
用数学式子表示为公式（6-1）。

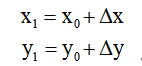
用矩阵表示如公式（6-2）所示：

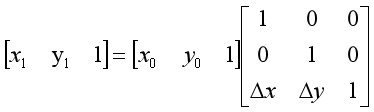
式子中，矩阵称为平移变换矩阵或因子，△x和△y称为平移量。图像平移首先定义平移矩阵M，再调用warpAffine()函数实现平移，核心函数如下：

• M = np.float32([[1, 0, x], [0, 1, y]])
  – M表示平移矩阵，其中x表示水平平移量，y表示垂直平移量
• shifted = cv2.warpAffine(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]])
  – src表示原始图像
  – M表示平移矩阵
  – dsize表示变换后的输出图像的尺寸大小
  – dst为输出图像，其大小为dsize，类型与src相同
  – flag表示插值方法的组合和可选值
  – borderValue表示像素外推法，当borderMode = BORDER_TRANSPARENT时，表示目标图像中的像素不会修改源图像中的“异常值”。
  – borderValue用于边界不变的情况，默认情况下为0

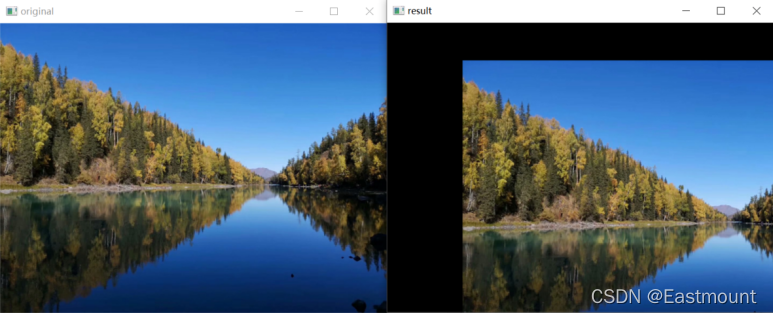
下面代码是图像平移的一个简单案例，它定义了图像平移矩阵M，然后调用warpAffine()函数将原始图像垂直向下平移了50个像素，水平向右平移了100个像素。

# -*- coding:utf-8 -*-
# By：Eastmount
import cv2
import numpy as np

#读取图片
src = cv2.imread('scenery.png')

#图像平移矩阵
M = np.float32([[1, 0, 100], [0, 1, 50]])

#获取原始图像列数和行数
rows, cols = src.shape[:2]

#图像平移
result = cv2.warpAffine(src, M, (cols, rows)) 

#显示图像
cv2.imshow("original", src)
cv2.imshow("result", result)

#等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

输出结果如图6-3所示：

下面一个案例是将图像分别向下、向上、向右、向左平移，再调用matplotlib绘图库依次绘制的过程。

# -*- coding:utf-8 -*-
# By：Eastmount
import cv2  
import numpy as np
import matplotlib.pyplot as plt
 
#读取图片
img = cv2.imread('scenery.png')
image = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)

#图像平移
#垂直方向 向下平移100
M = np.float32([[1, 0, 0], [0, 1, 100]])
img1 = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

#垂直方向 向上平移100
M = np.float32([[1, 0, 0], [0, 1, -100]])
img2 = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

#水平方向 向右平移100
M = np.float32([[1, 0, 100], [0, 1, 0]])
img3 = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

#水平方向 向左平移100
M = np.float32([[1, 0, -100], [0, 1, 0]])
img4 = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

#循环显示图形
titles = [ 'Image1', 'Image2', 'Image3', 'Image4']  
images = [img1, img2, img3, img4]  
for i in range(4):  
   plt.subplot(2,2,i+1), plt.imshow(images[i], 'gray')  
   plt.title(titles[i])  
   plt.xticks([]),plt.yticks([])  
plt.show()

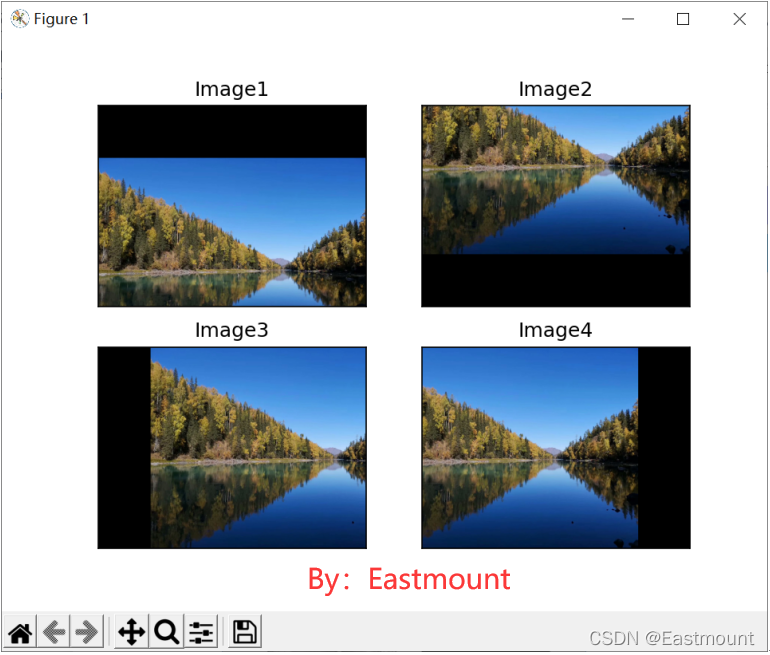
输出结果如图6-4所示，它从四个方向都进行了平移，并且调用subplot()函数将四个子图绘制在一起。

三.图像缩放

图像缩放（image scaling）是指对数字图像的大小进行调整的过程。在Python中，图像缩放主要调用resize()函数实现，函数原型如下：

• result = cv2.resize(src, dsize[, result[. fx[, fy[, interpolation]]]])
  – src表示原始图像
  – dsize表示图像缩放的大小
  – result表示图像结果
  – fx表示图像x轴方向缩放大小的倍数
  – fy表示图像y轴方向缩放大小的倍数
  – interpolation表示变换方法。CV_INTER_NN表示最近邻插值；CV_INTER_LINEAR表示双线性插值（缺省使用）；CV_INTER_AREA表示使用像素关系重采样，当图像缩小时，该方法可以避免波纹出现，当图像放大时，类似于CV_INTER_NN；CV_INTER_CUBIC表示立方插值

常见的图像缩放两种方式如下所示，第一种方式是将原图像设置为(160, 160)像素大小，第二种方式是将原始图像缩小为0.5倍。

• result = cv2.resize(src, (160,160))
• result = cv2.resize(src, None, fx=0.5, fy=0.5)

设(x1, y1)是缩放后的坐标，(x0, y0)是缩放前的坐标，sx、sy为缩放因子，则图像缩放的计算公式（6-3）所示：

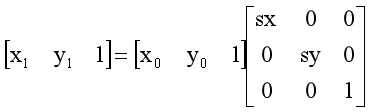
下面是Python实现图像缩放的代码，它将所读取的风景图像进行缩小。

# -*- coding:utf-8 -*-
# By：Eastmount
import cv2  
import numpy as np  
 
#读取图片
src = cv2.imread('scenery.png')

#图像缩放
result = cv2.resize(src, (200,100))
print(result.shape)

#显示图像
cv2.imshow("original", src)
cv2.imshow("result", result)

#等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

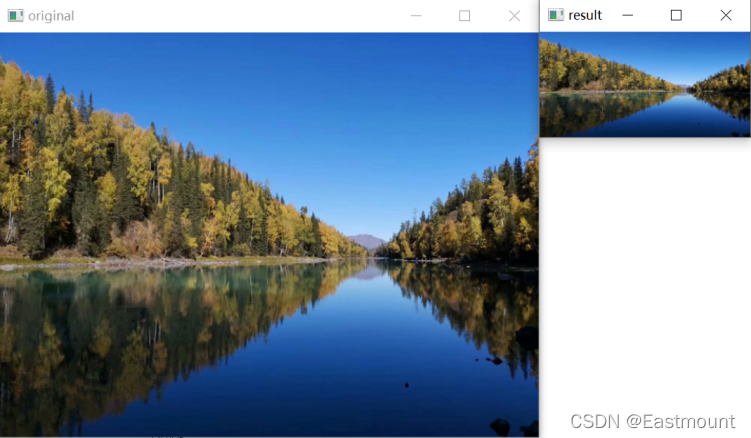
输出结果如图6-5所示，图像缩小为(100, 200, 3)像素。注意，代码中调用函数 cv2.resize(src, (200,100)) 设置新图像大小dsize的列数为200，行数为100。

下面讲解另一种图像缩放变换的方法，通过原始图像像素乘以缩放系数进行图像变换，代码如下：

# -*- coding:utf-8 -*-
# By：Eastmount
import cv2  
import numpy as np  
 
#读取图片
src = cv2.imread('scenery.png')
rows, cols = src.shape[:2]
print(rows, cols)

#图像缩放 dsize(列,行)
result = cv2.resize(src, (int(cols*0.6), int(rows*1.2)))

#显示图像
cv2.imshow("src", src)
cv2.imshow("result", result)
cv2.waitKey(0)
cv2.destroyAllWindows()

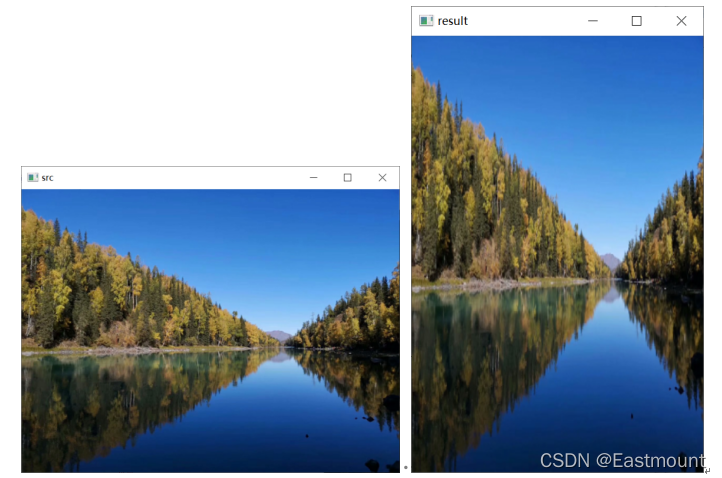
获取图片“scenery.png”的元素像素值，其rows值为384，cols值为512，接着进行宽度缩小0.6倍、高度放大1.2倍的处理，运行前后对比效果如图6-6所示。

最后讲解调用(fx,fy)参数设置缩放倍数的方法，对原始图像进行放大或缩小操作。下面代码是fx和fy方向缩小至原始图像0.3倍的操作。

# -*- coding:utf-8 -*-
# By：Eastmount
import cv2  
import numpy as np  
 
#读取图片
src = cv2.imread('scenery.png')
rows, cols = src.shape[:2]
print(rows, cols)

#图像缩放
result = cv2.resize(src, None, fx=0.3, fy=0.3)

#显示图像
cv2.imshow("src", src)
cv2.imshow("result", result)

#等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

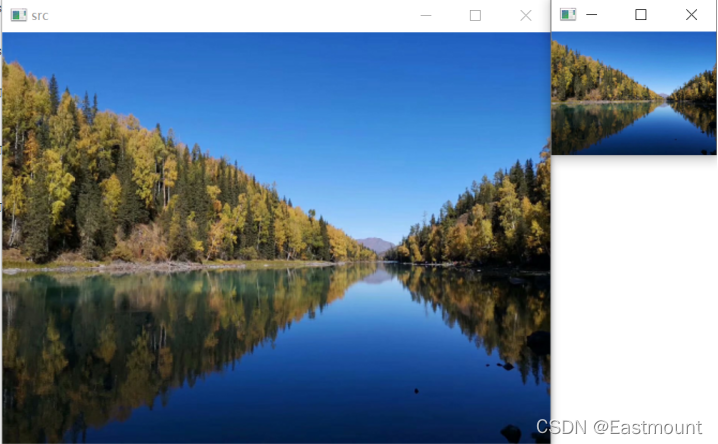
输出的结果如图6-7所示，这是按比例0.3×0.3缩小的。

四.图像旋转

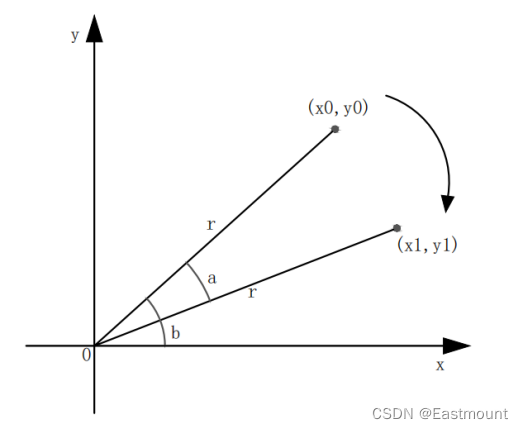
图像旋转是指图像以某一点为中心旋转一定的角度，形成一幅新的图像的过程。图像旋转变换会有一个旋转中心，这个旋转中心一般为图像的中心，旋转之后图像的大小一般会发生改变。图6-8表示原始图像的坐标(x0, y0)旋转至(x1, y1)的过程。

旋转公式如（6-4）所示，其中(m,n)是旋转中心，a是旋转的角度，(left,top)是旋转后图像的左上角坐标。

图像旋转变换主要调用getRotationMatrix2D()函数和warpAffine()函数实现，绕图像的中心旋转，函数原型如下：

• M = cv2.getRotationMatrix2D(center, angle, scale)
  – center表示旋转中心点，通常设置为(cols/2, rows/2)
  – angle表示旋转角度，正值表示逆时针旋转，坐标原点被定为左上角
  – scale表示比例因子

• rotated = cv2.warpAffine(src, M, (cols, rows))
  – src表示原始图像
  – M表示旋转参数，即getRotationMatrix2D()函数定义的结果
  – (cols, rows)表示原始图像的宽度和高度

实现代码如下所示：

# -*- coding:utf-8 -*-
# By：Eastmount
import cv2  
import numpy as np  
 
#读取图片
src = cv2.imread('scenery.png')

#源图像的高、宽 以及通道数
rows, cols, channel = src.shape

#绕图像的中心旋转
#函数参数：旋转中心 旋转度数 scale
M = cv2.getRotationMatrix2D((cols/2, rows/2), 30, 1)

#函数参数：原始图像 旋转参数 元素图像宽高
rotated = cv2.warpAffine(src, M, (cols, rows))  

#显示图像
cv2.imshow("src", src)
cv2.imshow("rotated", rotated)

#等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

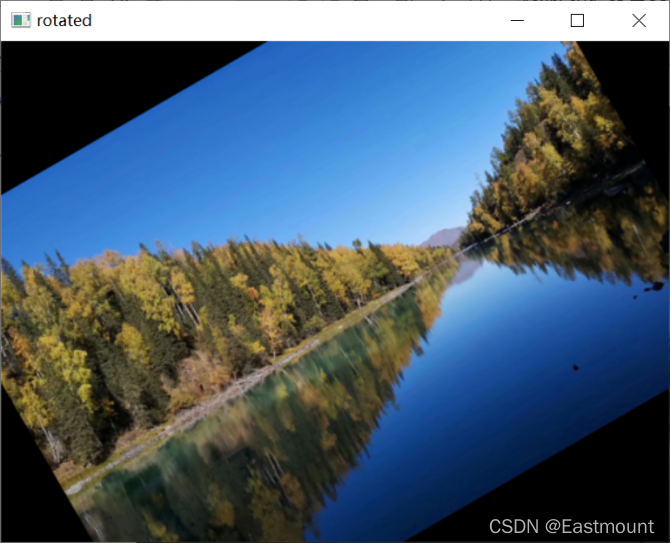
显示效果如图6-9所示，绕图像中心点逆时针旋转30度。

五.总结

本章主要讲解Python和OpenCV的图像几何变换，详细介绍了图像平移、图像缩放和图像旋转，这些知识点也是我们PC端或手机端图像处理应用常见的算法，读者可以尝试结合这些应用完成一套图像处理软件。

最近寒假日更，为了感谢读者。同时感谢在求学路上的同行者，不负遇见，勿忘初心。图像处理系列主要包括三部分，分别是：

感恩能与大家在华为云遇见！
希望能与大家一起在华为云社区共同成长，原文地址：https://blog.csdn.net/Eastmount/article/details/122723951

(By:娜璋之家 Eastmount 2022-04-24 夜于武汉)

参考文献：

• [1]冈萨雷斯. 数字图像处理（第3版）[M]. 北京：电子工业出版社, 2013.
• [2]阮秋琦. 数字图像处理学（第3版）[M]. 北京：电子工业出版社，2008.
• [3]毛星云, 冷雪飞. OpenCV3编程入门[M]. 北京：电子工业出版社, 2015.
• [4]Eastmount. [Python图像处理] 六.图像缩放、图像旋转、图像翻转与图像平移[EB/OL]. (2018-09-06). https://blog.csdn.net/Eastmount/article/details/82454335.
• [5]Eastmount. [数字图像处理] 六.MFC空间几何变换之图像平移、镜像、旋转、缩放详解[EB/OL]. (2015-06-04). https://blog.csdn.net/Eastmount/article/details/46345299.