[Python从零到壹] 十四.机器学习之分类算法五万字总结全网首发(决策树、KNN、SVM、分类对比实验) 丨【百变AI秀】
欢迎大家来到“Python从零到壹”,在这里我将分享约200篇Python系列文章,带大家一起去学习和玩耍,看看Python这个有趣的世界。所有文章都将结合案例、代码和作者的经验讲解,真心想把自己近十年的编程经验分享给大家,希望对您有所帮助,文章中不足之处也请海涵。Python系列整体框架包括基础语法10篇、网络爬虫30篇、可视化分析10篇、机器学习20篇、大数据分析20篇、图像识别30篇、人工智能40篇、Python安全20篇、其他技巧10篇。您的关注、点赞和转发就是对秀璋最大的支持,知识无价人有情,希望我们都能在人生路上开心快乐、共同成长。
前一篇文章讲述了聚类算法的原理知识级案例,包括K-Means聚类、BIRCH算法、PCA降维聚类、均值漂移聚类、文本聚类等。本文将详细讲解分类算法的原理知识级案例,包括决策树、KNN、SVM,并通过详细的分类对比实验和可视化边界分析与大家总结。四万字基础文章,希望对您有所帮助。
文章目录
下载地址:
前文赏析:
第一部分 基础语法
第二部分 网络爬虫
第三部分 数据分析+机器学习
- [Python从零到壹] 十三.机器学习之聚类分析万字总结全网首发(K-Means、BIRCH、层次聚类、树状聚类)
- [Python从零到壹] 十四.机器学习之分类算法五万字总结全网首发(决策树、KNN、SVM、分类对比实验)
分类(Classification)属于有监督学习(Supervised Learning)中的一类,它是数据挖掘、机器学习和数据科学中一个重要的研究领域。分类模型类似于人类学习的方式,通过对历史数据或训练集的学习得到一个目标函数,再用该目标函数预测新数据集的未知属性。本章主要讲述分类算法基础概念,并结合决策树、KNN、SVM分类算法案例分析各类数据集,从而让读者学会使用Python分类算法分析自己的数据集,研究自己领域的知识,从而创造价值。
与前面讲述的聚类模型类似,分类算法的模型如图1所示。它主要包括两个步骤:
- 训练。给定一个数据集,每个样本包含一组特征和一个类别信息,然后调用分类算法训练分类模型。
- 预测。利用生成的模型或函数对新的数据集(测试集)进行分类预测,并判断其分类后的结果,并进行可视化绘图显示。
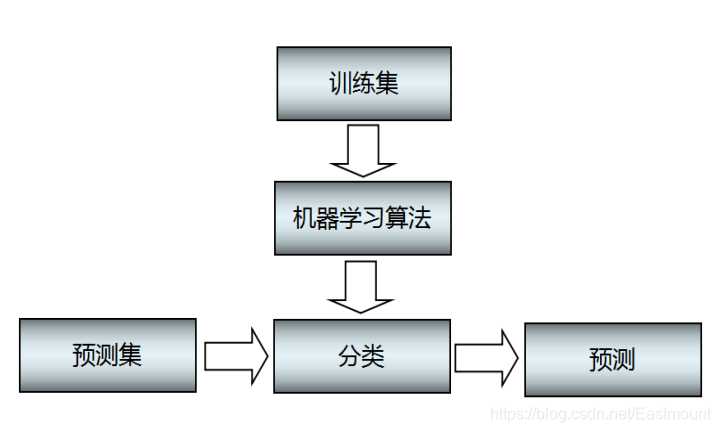
通常为了检验学习模型的性能,会使用校验集。数据集会被分成不相交的训练集和测试集,训练集用来构造分类模型,测试集用来检验多少类标签被正确分类。
下面举一个分类实例进行讲解。假设存在一个垃圾分类系统,将邮件划分为“垃圾邮件”和“非垃圾邮件”,现在有一个带有是否是垃圾邮件类标的训练集,然后训练一个分类模型,对测试集进行预测,步骤如下:
- (1) 分类模型对训练集进行训练,判断每行数据是正向数据还是负向数据,并不断与真实的结果进行比较,反复训练模型,直到模型达到某个状态或超出某个阈值,模型训练结束。
- (2) 利用该模型对测试集进行预测,判断其类标是“垃圾邮件”还是“非垃圾邮件”,并计算出该分类模型的准确率、召回率和F特征值。
经过上述步骤,当收到一封新邮件时,我们可以根据它邮件的内容或特征,判断其是否是垃圾邮件,这为我们提供了很大的便利,能够防止垃圾邮件信息的骚扰。
监督式学习包括分类和回归。其中常见的分类算法包括朴素贝叶斯分类器、决策树、K最近邻分类算法、支持向量机、神经网络和基于规则的分类算法等,同时还有用于组合单一类方法的集成学习算法,如Bagging和Boosting等。
(1) 朴素贝叶斯分类器
朴素贝叶斯分类器(Naive Bayes Classifier,简称NBC)发源于古典数学理论,有着坚实的数学基础和稳定的分类效率。该算法是利用Bayes定理来预测一个未知类别的样本属于各个类别的可能性,选择其中可能性最大的一个类别作为该样本的最终类别。其中,朴素贝叶斯(Naive Bayes)法是基于贝叶斯定理与特征条件独立假设的方法 ,是一类利用概率统计知识进行分类的算法,该算法被广泛应用的模型称为朴素贝叶斯模型(Naive Bayesian Model,简称NBM)。
根据贝叶斯定理,对于一个分类问题,给定样本特征x,样本属于类别y的概率如下:
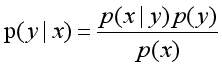
其中p(x)表示x事件发生的概率,p(y)表示y事件发生的概率,p(x|y)表示事件y发生后事件x发生的概率。由于贝叶斯定理的成立本身需要一个很强的条件独立性假设前提,而此假设在实际情况中经常是不成立的,因而其分类准确性就会下降,同时它对缺失的数据不太敏感。本书没有详细介绍朴素贝叶斯分类实例,希望读者下来自行研究学习。
(2) 决策树算法
决策树(Decision Tree)是以实例为基础的归纳学习(Inductive Learning)算法,它是对一组无次序、无规则的实例建立一棵决策判断树,并推理出树形结果的分类规则。决策树作为分类和预测的主要技术之一,其构造目的是找出属性和类别间的关系,用它来预测未知数据的类别。该算法采用自顶向下的递归方式,在决策树的内部节点进行属性比较,并根据不同属性值判断从该节点向下的分支,在决策树的叶子节点得到反馈的结果。
决策树算法根据数据的属性采用树状结构建立决策模型,常用来解决分类和回归问题。常见的算法包括:分类及回归树、ID3 、C4.5、随机森林等。
(3) K最近邻分类算法
K最近邻(K-Nearest Neighbor,简称KNN)分类算法是一种基于实例的分类方法,是数据挖掘分类技术中最简单常用的方法之一。所谓K最近邻,就是寻找K个最近的邻居,每个样本都可以用它最接近的K个邻居来代表。该方法需要找出与未知样本X距离最近的K个训练样本,看这K个样本中属于哪一类的数量多,就把未知样本X归为那一类。
K-近邻方法是一种懒惰学习方法,它存放样本,直到需要分类时才进行分类,如果样本集比较复杂,可能会导致很大的计算开销,因此无法应用到实时性很强的场合。
(4) 支持向量机
支持向量机(Support Vector Machine,简称SVM)是数学家Vapnik等人根据统计学习理论提出的一种新的学习方法,其基本模型定义为特征空间上间隔最大的线性分类器,其学习策略是间隔最大化,最终转换为一个凸二次规划问题的求解。
SVM算法的最大特点是根据结构风险最小化准则,以最大化分类间隔构造最优分类超平面来提高学习机的泛化能力,较好地解决了非线性、高维数、局部极小点等问题,同时维数大于样本数时仍然有效,支持不同的内核函数(线性、多项式、s型等)。
(5) 神经网络
神经网络(Neural Network,也称之为人工神经网络)算法是80年代机器学习界非常流行的算法,不过在90年代中途衰落。现在又随着“深度学习”之势重新火热,成为最强大的机器学习算法之一。图2是一个神经网络的例子,包括输入层、隐藏层和输出层。
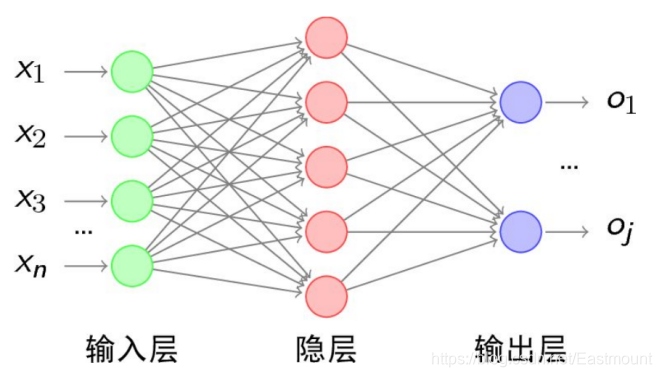
人工神经网络(Artificial Neural Network,简称ANN)是一种模仿生物神经网络的结构和功能的数学模型或计算模型。在这种模型中,大量的节点或称“神经元”之间相互联接构成网络,即“神经网络”,以达到处理信息的目的。神经网络通常需要进行训练,训练的过程就是网络进行学习的过程,训练改变了网络节点的连接权的值使其具有分类的功能,经过训练的网络就可用于对象的识别。
常见的人工神经网络有BP(Back Propagation)神经网络、径向基RBF神经网络、Hopfield神经网络、随机神经网络(Boltzmann机)、深度神经网络DNN、卷积神经网络CNN等。
(6) 集成学习
集成学习(Ensemble Learning)是一种机器学习方法,它使用一系列学习器进行学习,并使用某种规则把各个学习结果进行整合从而获得比单个学习器更好的学习效果。由于实际应用的复杂性和数据的多样性往往使得单一的分类方法不够有效,因此,学者们对多种分类方法的融合即集成学习进行了广泛的研究,它已俨然成为了国际机器学习界的研究热点。
集成学习试图通过连续调用单个的学习算法,获得不同的基学习器,然后根据规则组合这些学习器来解决同一个问题,可以显著的提高学习系统的泛化能力。组合多个基学习器主要采用投票(加权)的方法,常见的算法有装袋(Bagging)、推进(Boosting)等。
在第12篇文章中我们详细讲解了回归分析,13篇详细讲解了聚类分析,本章着重讲解分类分析,而它们之间究竟存在什么区别和关系呢?
- 分类(Classification)和回归(Regression)都属于监督学习,它们的区别在于:回归是用来预测连续的实数值,比如给定了房屋面积,来预测房屋价格,返回的结果是房屋价格;而分类是用来预测有限的离散值,比如判断一个人是否患糖尿病,返回值是“是”或“否”。即明确对象属于哪个预定义的目标类,预定义的目标类是离散时为分类,连续时为回归。
- 分类属于监督学习,而聚类属于无监督学习,其主要区别是:训练过程中是否知道结果或是否存在类标。比如让小孩给水果分类,给他苹果时告诉他这是苹果,给他桃子时告诉他这是桃子,经过反复训练学习,现在给他一个新的水果,问他“这是什么?”,小孩对其进行回答判断,整个过程就是一个分类学习的过程,在训练小孩的过程中反复告诉他对应水果真实的类别。而如果采用聚类算法对其进行分析,则是给小孩一堆水果,包括苹果、橘子、桃子,小孩开始不知道需要分类的水果是什么,让小孩自己对水果进行分类,按照水果自身的特征进行归纳和判断,小孩分成三堆后,再给小孩新的水果,比如是苹果,小孩把它放到苹果堆的整个过程称之为聚类学习过程。
总之,分类学习在训练过程中是知道对应的类标结果的,即训练集是存在对应的类标的;而聚类学习在训练过程中不知道数据对应的结果,根据数据集的特征特点,按照“物以类聚”的方法,将具有相似属性的数据聚集在一起。
分类算法有很多,不同的分类算法又有很多不同的变种,不同的分类算法有不同的特点,在不同的数据集上表现的效果也不同,我们需要根据特定的任务来选择对应的算法。选择好了分类算法之后,我们如何评价一个分类算法的好坏呢?
本书主要采用精确率(Precision)、召回率(Recall)和F值(F-measure或F-score)来评价分类算法。
(1) 精确率(Precision)和召回率(Recall)
精确率定义为检索出相关文档数与检索出的文档总数的比率,衡量的是检索系统的查准率;召回率定义为检索出的相关文档数和文档库中所有相关文档数的比率,衡量的是检索系统的查全率。公式如下:
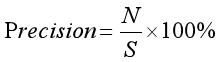
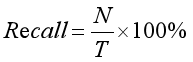
其中,参数N表示实验结果中正确识别出的聚类类簇数,S表示实验结果中实际识别出的聚类类簇数,T表示数据集中所有真实存在的聚类相关类簇数。
(2) F值(F-measure或F-score)
精确率和召回率两个评估指标在特定的情况下是相互制约的,因而很难使用单一的评价指标来衡量实验的效果。F-值是准确率和召回率的调和平均值,它可作为衡量实验结果的最终评价指标,F值更接近两个数中较小的那个。F值指的计算公式如下公式所示:
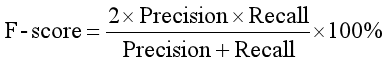
(3) 其他指标
其他常用的分类算法的评价指标包括:
- 准确率(Accuracy)
- 错误率(Error Rate)
- 灵敏度(Sensitive)
- 特效度(Specificity)
- ROC曲线
- …
下面通过一个招聘的案例讲述决策树的基本原理及过程。假设一位程序员与面试官的初次面试的简单对话,我们利用决策树分类的思想来构建一棵树形结构。对话如下:
面试官:多大年纪了?
程序员:25岁。
面试官:本科是不是已经毕业呢?
程序员:是的。
面试官:编程技术厉不厉害?
程序员:不算太厉害,中等水平。
面试官:熟悉Python语言吗?
程序员:熟悉的,做过数据挖掘相关应用。
面试官:可以的,你通过了。
这个面试的决策过程就是典型的分类树决策。相当于通过年龄、学历、编程技术和是否熟悉Python语言将程序员初试分为两个类别:通过和不通过。假设这个面试官对程序员的要求是30岁以下、学历本科以上并且是编程厉害或熟悉Pyhon语言中等以上编程技术的程序员,这个面试官的决策逻辑过程用图3表示。
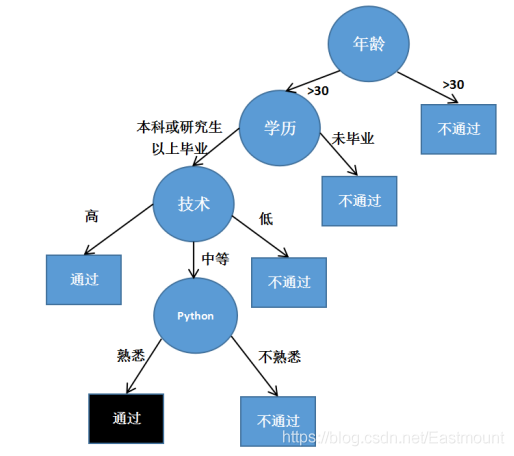
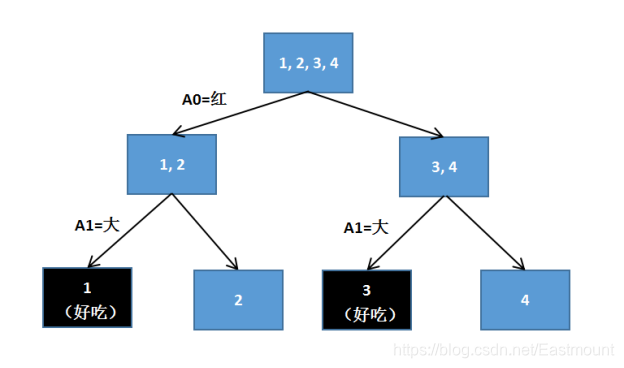
第二个实例是典型的决策树判断苹果的例子,假设存在4个样本,2个属性判断是否是好苹果,其中第二列1表示苹果很红,0表示苹果不红;第三列1表示苹果很大,0表示苹果很小;第4列结果1表示苹果好吃,0表示苹果不好吃。
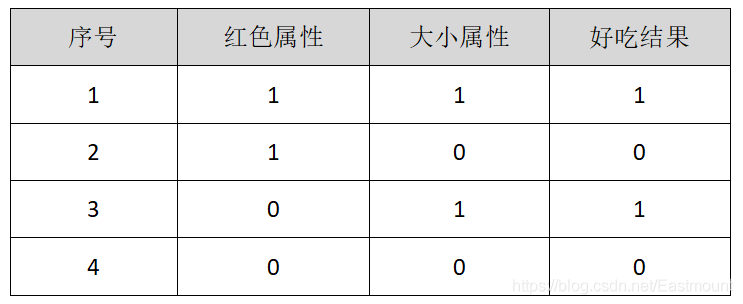
样本中有2个属性,即苹果红色属性和苹果大小属性。这里红苹果用A0表示,大苹果用A1表示,构建的决策树如图19.4所示。图中最顶端有四个苹果(1、2、3、4),然后它将颜色红的苹果放在一边(A0=红),颜色不红的苹果放在另一边,其结果为1、2是红苹果,3、4是不红的苹果;再根据苹果的大小进行划分,将大的苹果判断为好吃的(A1=大),最终输出结果在图中第三层显示,其中1和3是好吃的苹果,2和4是不好吃的苹果,该实例表明苹果越大越好吃。
决策树算法根据数据的属性并采用树状结构构建决策模型,常用来解决分类和回归问题。常见的决策树算法包括:
- 分类及回归树(Classification And Regression Tree,简称CART)
- ID3算法(Iterative Dichotomiser 3)
- C4.5算法
- 随机森林算法(Random Forest)
- 梯度推进机算法(Gradient Boosting Machine,简称GBM)
决策树构建的基本步骤包括4步,具体步骤如下:
- 第一步:开始时将所有记录看作一个节点。
- 第二步:遍历每个变量的每一种分割方式,找到最好的分割点。
- 第三步:分割成两个节点N1和N2。
- 第四步:对N1和N2分别继续执行第二步和第三步,直到每个节点足够“纯”为止。
决策数具有两个优点:
- 模型可以读性好,描述性强,有助于人工分析。
- 效率高,决策树只需要一次构建,可以被反复使用,每一次预测的最大计算次数不超过决策树的深度。
Sklearn机器学习包中,实现决策树(DecisionTreeClassifier,简称DTC)的类是:
- sklearn.tree.DecisionTreeClassifier
它能够解决数据集的多类分类问题,输入参数为两个数组X[n_samples,n_features]和y[n_samples],X为训练数据,y为训练数据标记值。DecisionTreeClassifier构造方法为:
sklearn.tree.DecisionTreeClassifier(criterion='gini'
, splitter='best'
, max_depth=None
, min_samples_split=2
, min_samples_leaf=1
, max_features=None
, random_state=None
, min_density=None
, compute_importances=None
, max_leaf_nodes=None)
DecisionTreeClassifier类主要包括两个方法:
- clf.fit(train_data, train_target)
用来装载(train_data,train_target)训练数据,并训练分类模型。 - pre = clf.predict(test_data)
用训练得到的决策树模型对test_data测试集进行预测分析。
前面第12篇文章介绍过逻辑回归分析鸢尾花的实例,这里再次讲解决策树分析鸢尾花实例,从而加深读者印象。
(1) 数据集回顾
在Sklearn机器学习包中,集成了各种各样的数据集,包括糖尿病数据集、鸢尾花数据集、新闻数据集等。这里使用的是鸢尾花卉Iris数据集,它是一个很常用的数据集,共150行数据,包括四个特征变量:
- 萼片长度
- 萼片宽度
- 花瓣长度
- 花瓣宽度。
同时包括一个类别变量,将鸢尾花划分为三个类别,即:
- 山鸢尾(Iris-setosa)
- 变色鸢尾(Iris-versicolor)
- 维吉尼亚鸢尾(Iris-virginica)
表2为鸢尾花数据集,详细信息如下表所示。
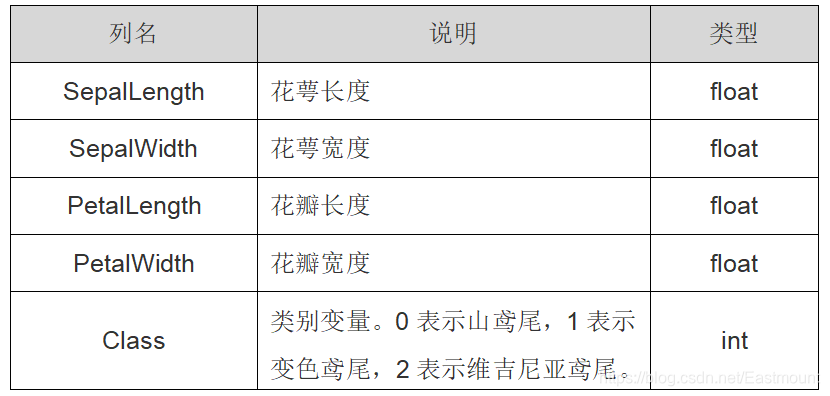
iris是鸢尾植物,这里存储了其萼片和花瓣的长宽,共4个属性,鸢尾植物分三类。 iris数据集中包括两个属性iris.data和iris.target。其中,data数据是一个矩阵,每一列代表了萼片或花瓣的长宽,一共4列,每一行数据代表某个被测量的鸢尾植物,一共采样了150条记录。载入鸢尾花数据集代码如下所示:
from sklearn.datasets import load_iris
iris = load_iris()
print(iris.data)
print(iris.target)

(2) 决策树简单分析鸢尾花
下述代码实现了调用Sklearn机器学习包中DecisionTreeClassifier决策树算法进行分类分析,并绘制预测的散点图。
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-07-06
#导入数据集iris
from sklearn.datasets import load_iris
iris = load_iris()
print(iris.data) #输出数据集
print(iris.target) #输出真实标签
print(len(iris.target))
print(iris.data.shape) #150个样本 每个样本4个特征
#导入决策树DTC包
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()
clf.fit(iris.data, iris.target) #训练
print(clf)
predicted = clf.predict(iris.data) #预测
#获取花卉两列数据集
X = iris.data
L1 = [x[0] for x in X]
L2 = [x[1] for x in X]
#绘图
import numpy as np
import matplotlib.pyplot as plt
plt.scatter(L1, L2, c=predicted, marker='x') #cmap=plt.cm.Paired
plt.title("DTC")
plt.show()
输出结果如图5所示,可以看到决策树算法将数据集预测为三类,分别代表着数据集对应的三种鸢尾花,但数据集中存在小部分交叉结果。预测的结果如下:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
150
(150, 4)
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False,
random_state=None, splitter='best')
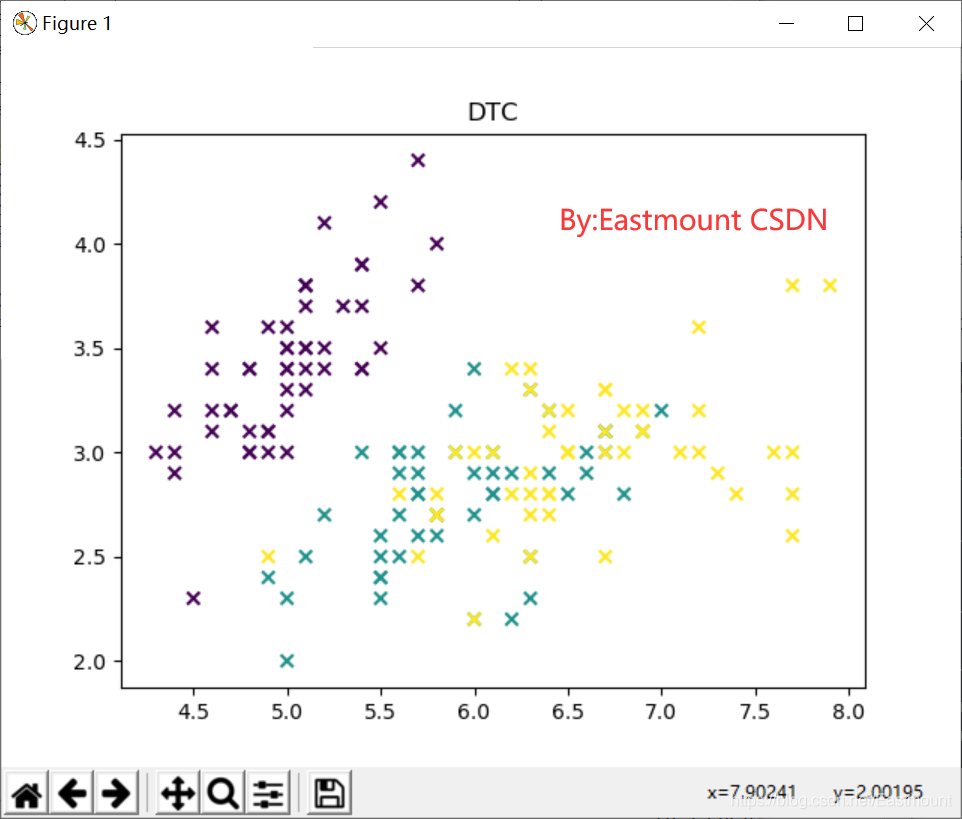
下面对上述核心代码进行简单描述。
- from sklearn.datasets import load_iris
- iris = load_iris()
该部分代码是导入sklearn机器学习包自带的鸢尾花数据集,调用load_iris()函数导入数据,数据共分为数据(data)和类标(target)两部分。
- from sklearn.tree import DecisionTreeClassifier
- clf = DecisionTreeClassifier()
- clf.fit(iris.data, iris.target)
- predicted = clf.predict(iris.data)
该部分代码导入决策树模型,并调用fit()函数进行训练,predict()函数进行预测。
- import matplotlib.pyplot as plt
- plt.scatter(L1, L2, c=predicted, marker=‘x’)
该部分代码是导入matplotlib绘图扩展包,调用scatter()函数绘制散点图。
但上面的代码中存在两个问题:
- 代码中通过“L1 = [x[0] for x in X]”获取了第一列和第二列数据集进行了分类分析和绘图,而真实的iris数据集中包括四个特征,那怎么绘制四个特征的图形呢? 这就需要利用PCA降维技术处理,参考前一篇文章。
- 第二个问题是在聚类、回归、分类模型中,都需要先进行训练,再对新的数据集进行预测,这里却是对整个数据集进行分类分析,而真实情况是需要把数据集划分为训练集和测试集的,例如数据集的70%用于训练、30%用于预测,或80%用于训练、20%用于预测。
这部分内容主要是进行代码优化,将数据集划分为80%训练集-20%预测集,并对决策树分类算法进行评估。由于提供的数据集类标是存在一定规律的,前50个类标为0(山鸢尾)、中间50个类标为1(变色鸢尾)、最后50个类标为2(维吉尼亚鸢)。即:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
这里调用NumPy库中的 concatenate() 函数对数据集进行挑选集成,选择第0-40行、第50-90行、第100-140行数据作为训练集,对应的类标作为训练样本类标;再选择第40-50行、第90-100行、第140-150行数据作为测试集合,对应的样本类标作为预测类标。
代码如下,“axis=0”表示选取数值的等差间隔为0,即紧挨着获取数值。
#训练集
train_data = np.concatenate((iris.data[0:40, :], iris.data[50:90, :], iris.data[100:140, :]), axis = 0)
#训练集样本类别
train_target = np.concatenate((iris.target[0:40], iris.target[50:90], iris.target[100:140]), axis = 0)
#测试集
test_data = np.concatenate((iris.data[40:50, :], iris.data[90:100, :], iris.data[140:150, :]), axis = 0)
#测试集样本类别
test_target = np.concatenate((iris.target[40:50], iris.target[90:100], iris.target[140:150]), axis = 0)
同时,调用sklearn机器学习包中metrics类对决策树分类算法进行评估,它将输出准确率(Precison)、召回率(Recall)、F特征值(F-score)、支持度(Support)等。
#输出准确率 召回率 F值
from sklearn import metrics
print(metrics.classification_report(test_target, predict_target))
print(metrics.confusion_matrix(test_target, predict_target))
分类报告的核心函数为:
sklearn.metrics.classification_report(y_true,
y_pred,
labels=None,
target_names=None,
sample_weight=None,
digits=2)
其中y_true参数表示正确的分类类标,y_pred表示分类预测的类标,labels表示分类报告中显示的类标签的索引列表,target_names参数显示与labels对应的名称,digits是指定输出格式的精确度。评价公式如下:
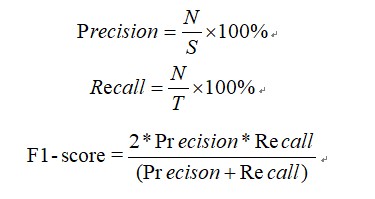
调用 metrics.classification_report() 方法对决策树算法进行评估后,会在最后一行将对所有指标进行加权平均值,详见下面完整代码。
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-07-06
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
import numpy as np
import matplotlib.pyplot as plt
#导入数据集iris
'''
重点:分割数据集 构造训练集/测试集,80/20
70%训练 0-40 50-90 100-140
30%预测 40-50 90-100 140-150
'''
iris = load_iris()
train_data = np.concatenate((iris.data[0:40, :], iris.data[50:90, :], iris.data[100:140, :]), axis = 0) #训练集
train_target = np.concatenate((iris.target[0:40], iris.target[50:90], iris.target[100:140]), axis = 0) #训练集样本类别
test_data = np.concatenate((iris.data[40:50, :], iris.data[90:100, :], iris.data[140:150, :]), axis = 0) #测试集
test_target = np.concatenate((iris.target[40:50], iris.target[90:100], iris.target[140:150]), axis = 0) #测试集样本类别
#导入决策树DTC包
clf = DecisionTreeClassifier()
clf.fit(train_data, train_target) #注意均使用训练数据集和样本类标
print(clf)
predict_target = clf.predict(test_data) #测试集
print(predict_target)
#预测结果与真实结果比对
print(sum(predict_target == test_target))
#输出准确率 召回率 F值
print(metrics.classification_report(test_target, predict_target))
print(metrics.confusion_matrix(test_target, predict_target))
#获取花卉测试数据集两列数据
X = test_data
L1 = [n[0] for n in X]
L2 = [n[1] for n in X]
#绘图
plt.scatter(L1, L2, c=predict_target, marker='x') #cmap=plt.cm.Paired
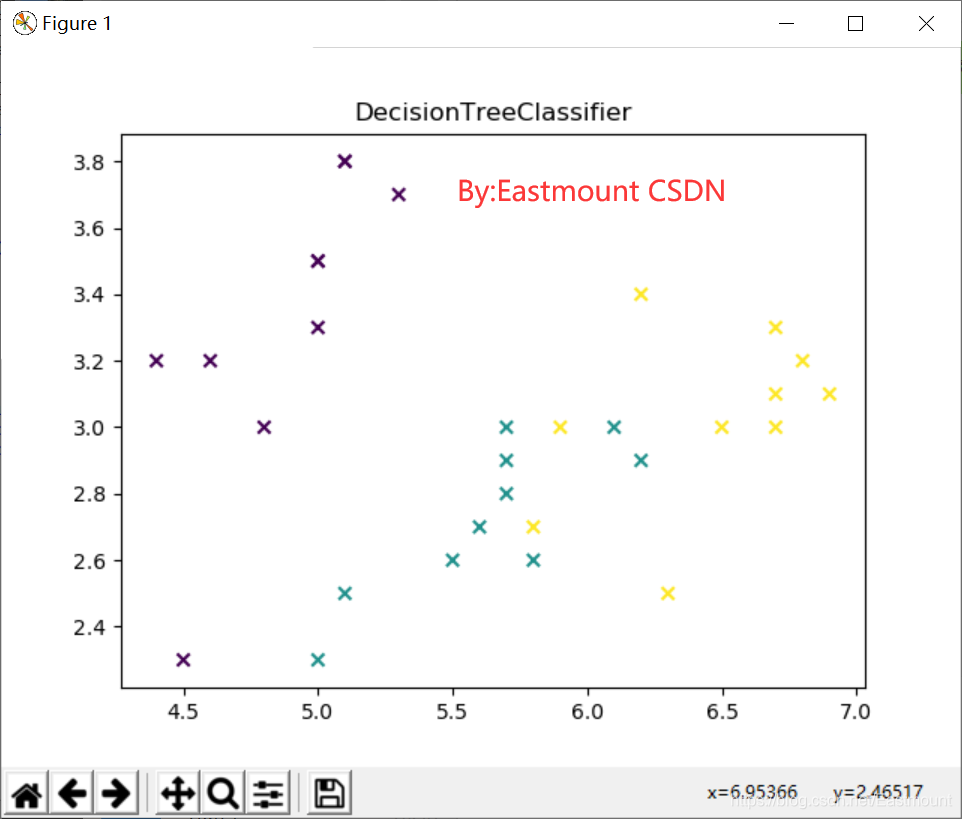
plt.title("DecisionTreeClassifier")
plt.show()
输出结果如下,包括对数据集40-50、90-100、140-150的预测结果,接下来输出的“30”表示整个30组类标预测结果和真实结果是一致的,最后输出评估结果。
[0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2]
30
precision recall f1-score support
0 1.00 1.00 1.00 10
1 1.00 1.00 1.00 10
2 1.00 1.00 1.00 10
avg / total 1.00 1.00 1.00 30
[[10 0 0]
[ 0 10 0]
[ 0 0 10]]
同时输出图形如图6所示。
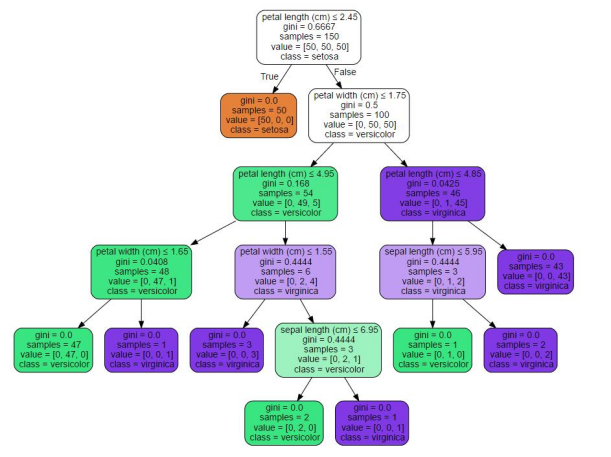
读者可以自行深入研究,调用sklearn.tree.export_graphviz类实现导出决策树绘制树形结构的过程,比如鸢尾花数据集输出如图7所示的树形结构。
下面讲述区域划分对比实验(前面已经出现过),它是指按照数据集真实的类标,将其划分为不同颜色区域,这里的鸢尾花数据集共分为三个区域,最后进行散点图绘制对比。每个区域对应一类散点,表示预测结果和真实结果一致,如果某个区域混入其他类型的散点,则表示该点的预测结果与真实结果不一致。
完整代码如下所示,代码首先调用“iris.data[:, :2]”代码获取其中两列数据(两个特征),再进行决策树分类分析。
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-07-06
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
#载入鸢尾花数据集
iris = load_iris()
X = X = iris.data[:, :2] #获取花卉前两列数据
Y = iris.target
lr = DecisionTreeClassifier()
lr.fit(X,Y)
#meshgrid函数生成两个网格矩阵
h = .02
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
#pcolormesh函数将xx,yy两个网格矩阵和对应的预测结果Z绘制在图片上
Z = lr.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(8,6))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
#绘制散点图
plt.scatter(X[:50,0], X[:50,1], color='red',marker='o', label='setosa')
plt.scatter(X[50:100,0], X[50:100,1], color='blue', marker='x', label='versicolor')
plt.scatter(X[100:,0], X[100:,1], color='green', marker='s', label='Virginica')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.legend(loc=2)
plt.show()
下面作者对区域划分对比代码进行详细讲解。
- x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
- y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
- xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
获取的鸢尾花两列数据,对应为萼片长度和萼片宽度,每个点的坐标就是(x,y)。先取X二维数组的第一列(长度)的最小值、最大值和步长h(设置为0.02)生成数组,再取X二维数组的第二列(宽度)的最小值、最大值和步长h生成数组,最后用meshgrid()函数生成两个网格矩阵xx和yy,如下所示:
[[ 3.8 3.82 3.84 ..., 8.36 8.38 8.4 ]
[ 3.8 3.82 3.84 ..., 8.36 8.38 8.4 ]
...,
[ 3.8 3.82 3.84 ..., 8.36 8.38 8.4 ]
[ 3.8 3.82 3.84 ..., 8.36 8.38 8.4 ]]
[[ 1.5 1.5 1.5 ..., 1.5 1.5 1.5 ]
[ 1.52 1.52 1.52 ..., 1.52 1.52 1.52]
...,
[ 4.88 4.88 4.88 ..., 4.88 4.88 4.88]
[ 4.9 4.9 4.9 ..., 4.9 4.9 4.9 ]]
- Z = lr.predict(np.c_[xx.ravel(), yy.ravel()])
调用ravel()函数将xx和yy的两个矩阵转变成一维数组,再进行预测分析。由于两个矩阵大小相等,因此两个一维数组大小也相等。np.c_[xx.ravel(), yy.ravel()]是生成矩阵,即:
xx.ravel()
[ 3.8 3.82 3.84 ..., 8.36 8.38 8.4 ]
yy.ravel()
[ 1.5 1.5 1.5 ..., 4.9 4.9 4.9]
np.c_[xx.ravel(), yy.ravel()]
[[ 3.8 1.5 ]
[ 3.82 1.5 ]
[ 3.84 1.5 ]
...,
[ 8.36 4.9 ]
[ 8.38 4.9 ]
[ 8.4 4.9 ]]
总之,上述操作是把第一列萼片长度数据按h取等分作为行,并复制多行得到xx网格矩阵;再把第二列萼片宽度数据按h取等分,作为列,并复制多列得到yy网格矩阵;最后将xx和yy矩阵都变成两个一维数组,调用np.c_[]函数组合成一个二维数组进行预测。
调用predict()函数进行预测,预测结果赋值给Z。即:
Z = logreg.predict(np.c_[xx.ravel(), yy.ravel()])
[1 1 1 ..., 2 2 2]
size: 39501
- Z = Z.reshape(xx.shape)
调用reshape()函数修改形状,将其Z转换为两个特征(长度和宽度),则39501个数据转换为171*231的矩阵。Z = Z.reshape(xx.shape)输出如下:
[[1 1 1 ..., 2 2 2]
[1 1 1 ..., 2 2 2]
[0 1 1 ..., 2 2 2]
...,
[0 0 0 ..., 2 2 2]
[0 0 0 ..., 2 2 2]
[0 0 0 ..., 2 2 2]]
- plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
调用pcolormesh()函数将xx、yy两个网格矩阵和对应的预测结果Z绘制在图片上,可以发现输出为三个颜色区块,分别表示三类区域。cmap=plt.cm.Paired表示绘图样式选择Paired主题。输出的区域如下图所示:
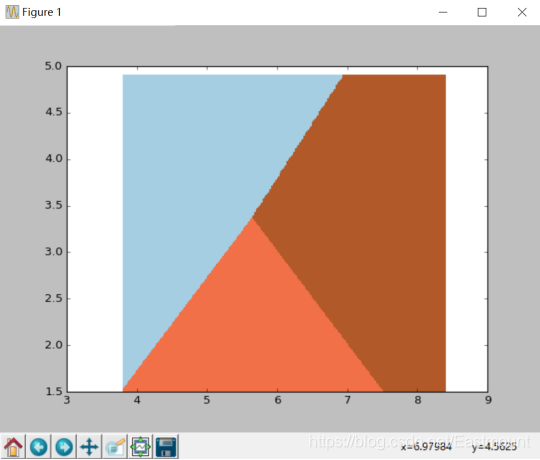
- plt.scatter(X[:50,0], X[:50,1], color=‘red’,marker=‘o’, label=‘setosa’)
调用scatter()绘制散点图,第一个参数为第一列数据(长度),第二个参数为第二列数据(宽度),第三、四个参数为设置点的颜色为红色,款式为圆圈,最后标记为setosa。
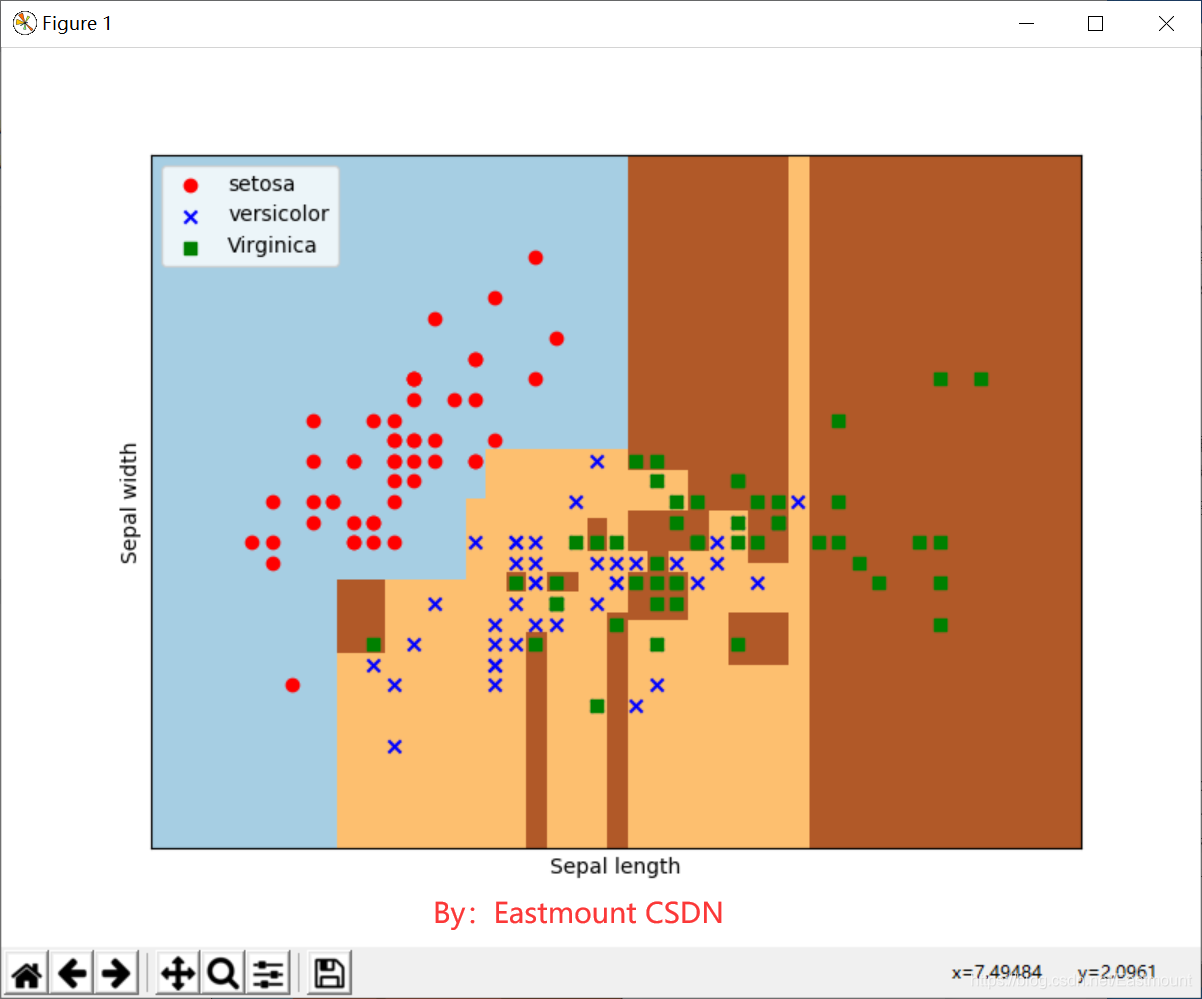
最终输出如图9所示,经过决策树分析后划分为三个区域,左上角部分为红色的圆点,对应setosa鸢尾花;右边部分为绿色方块,对应virginica鸢尾花;中间靠下部分为蓝色星形,对应versicolor鸢尾花。散点图为各数据点真实的花类型,划分的三个区域为数据点预测的花类型,预测的分类结果与训练数据的真实结果结果基本一致,部分鸢尾花出现交叉。
KNN分类算法是最近邻算法,字面意思就是寻找最近邻居,由Cover和Hart在1968年提出,它简单直观易于实现。下面通过一个经典例子来讲解如何寻找邻居,选取多少个邻居。图10需要判断右边这个动物是鸭子、鸡还是鹅?这就涉及到了KNN算法的核心思想,判断与这个样本点相似的类别,再预测其所属类别。由于它走路和叫声像一只鸭子,所以右边的动物很可能是一只鸭子。
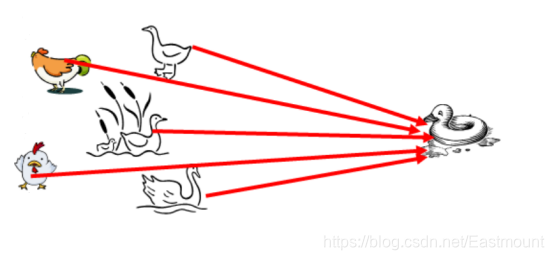
KNN分类算法的核心思想是从训练样本中寻找所有训练样本X中与测试样本距离(常用欧氏距离)最近的前K个样本(作为相似度),再选择与待分类样本距离最小的K个样本作为X的K个最邻近,并检测这K个样本大部分属于哪一类样本,则认为这个测试样本类别属于这一类样本。
KNN分类的算法步骤如下:
- 计算测试样本点到所有样本点的欧式距离dist,采用勾股定理计算
- 用户自定义设置参数K,并选择离带测点最近的K个点
- 从这K个点中,统计各个类型或类标的个数
- 选择出现频率最大的类标号作为未知样本的类标号,反馈最终预测结果
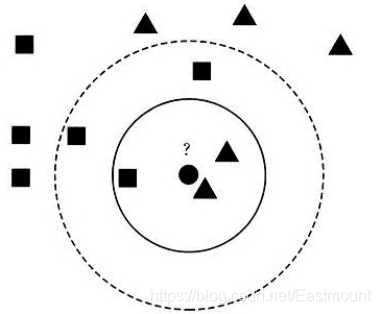
假设现在需要判断图11中的圆形图案属于三角形还是正方形类别,采用KNN算法分析步骤如下:
- 当K=3时,图中第一个圈包含了三个图形,其中三角形2个,正方形一个,该圆的则分类结果为三角形。
- 当K=5时,第二个圈中包含了5个图形,三角形2个,正方形3个,则以3:2的投票结果预测圆为正方形类标。
- 同理,当K=11原理也是一样,设置不同的K值,可能预测得到结果也不同。所以,KNN是一个非常简单、易于理解实现的分类算法。
最后简单讲述KNN算法的优缺点。KNN分类算法存在的优点包括:
- 算法思路较为简单,易于实现。
- 当有新样本要加入训练集中时,无需重新训练,即重新训练的代价低。
- 计算时间和空间线性于训练集的规模。
其缺点主要表现为分类速度慢,由于每次新的待分样本都必须与所有训练集一同计算比较相似度,以便取出靠前的K个已分类样本,所以时间复杂度较高。整个算法的时间复杂度可以用O(m*n)表示,其中m是选出的特征项的个数,而n是训练集样本的个数。同时,如果K值确定不好,也会影响整个实验的结果,这也是KNN算法的另一个缺点。
Sklearn机器学习包中,实现KNN分类算法的类是neighbors.KNeighborsClassifier。构造方法如下:
KNeighborsClassifier(algorithm='ball_tree',
leaf_size=30,
metric='minkowski',
metric_params=None,
n_jobs=1,
n_neighbors=3,
p=2,
weights='uniform')
其中最重要的参数是n_neighbors=3,设置最近邻K值。同时,KNeighborsClassifier可以设置3种算法:brute、kd_tree、ball_tree。具体调用方法如下:
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=3, algorithm="ball_tree")
KNN算法分析时也包括训练和预测两个方法。
- 训练:
knn.fit(data, target) - 预测:
pre = knn.predict(data)
下面这段代码是简单调用KNN分类算法进行预测的例子,代码如下。
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-07-06
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
X = np.array([[-1,-1],[-2,-2],[1,2], [1,1],[-3,-4],[3,2]])
Y = [0,0,1,1,0,1]
x = [[4,5],[-4,-3],[2,6]]
knn = KNeighborsClassifier(n_neighbors=3, algorithm="ball_tree")
knn.fit(X,Y)
pre = knn.predict(x)
print(pre)
定义了一个二维数组用于存储6个点,其中x和y坐标为负数的类标定义为0,x和y坐标为正数的类标定义为1。调用knn.fit(X,Y)函数训练模型后,再调用predict()函数预测[4,5]、[-4,-3]、[2,6]三个点的坐标,输出结果分别为:[1, 0, 1],其中x和y坐标为正数的划分为一类,负数的一类。
同时也可以计算K个最近点的下标和距离,代码和结果如下,其中,indices表示点的下标,distances表示距离。
distances, indices = knn.kneighbors(X)
print(indices)
print(distances)
>>>
[1 0 1]
[[0 1 3]
[1 0 4]
[2 3 5]
[3 2 5]
[4 1 0]
[5 2 3]]
[[ 0. 1.41421356 2.82842712]
[ 0. 1.41421356 2.23606798]
[ 0. 1. 2. ]
[ 0. 1. 2.23606798]
[ 0. 2.23606798 3.60555128]
[ 0. 2. 2.23606798]]
>>>
下面通过一个完整的实例结合可视化技术进行讲解,加深读者的印象。
(1) 数据集
该实验数据集是UCI Machine Learning Repository开源网站提供的MostPopular Data Sets(hits since 2007)红酒数据集,它是对意大利同一地区生产的三种不同品种的酒,做大量分析所得出的数据。这些数据包括了三种类别的酒,酒中共13种不同成分的特征,共178行数据,如图13所示。

该数据集包括了三种类型酒中13种不同成分的数量,13种成分分别是:Alcohol、Malicacid、Ash、Alcalinity of ash、Magnesium、Total phenols、Flavanoids、Nonflavanoid phenols、Proanthocyanins、Color intensity、Hue、OD280/OD315 of diluted wines和Proline,每一种成分可以看成一个特征,对应一个数据。三种类型的酒分别标记为“1”、“2”、“3”。数据集特征描述如表3所示。
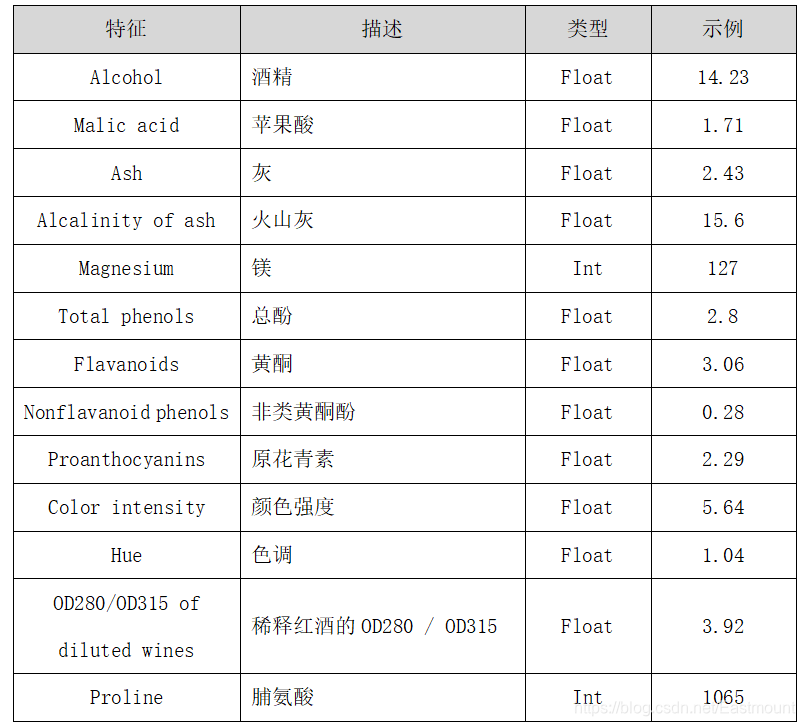
数据存储在wine.txt文件中,如图14所示。每行数据代表一个样本,共178行数据,每行数据包含14列,即第一列为类标属性,后面依次是13列特征。其中第1类有59个样本,第2类有71个样本,第3类有48个样本。
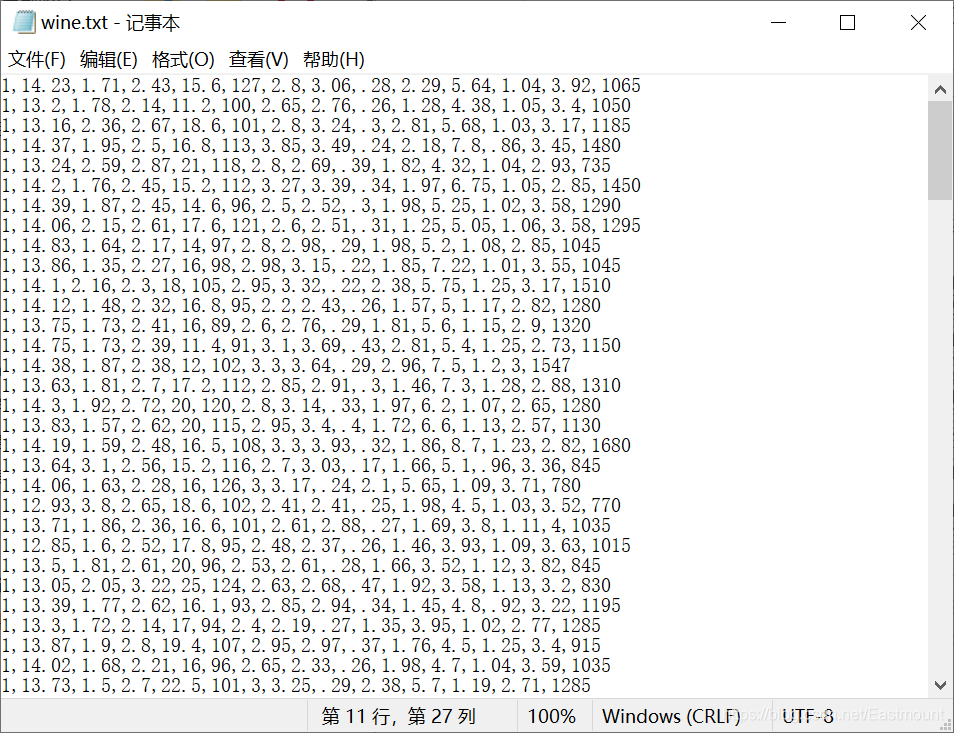
注意:前面讲述了如何读取CSV文件数据集或Sklearn扩展包所提供的数据集,但现实分析中,很多数据集会存储于TXT或DATA文件中,它们采用一定的符号进行分隔,比如图中采用逗号分隔,如何获取这类文件中的数据,也是非常重要的知识。所以接下来先教大家读取这类文件的数据。
(2) 读取数据集
从图14可以看到整个数据集采用逗号分隔,常用读取该类型数据集的方法是调用open()函数读取文件,依次读取TXT文件中所有内容,再按照逗号分割符获取每行的14列数据存储至数组或矩阵中,从而进行数据分析。这里讲述另一种方法,调用loadtxt()函数读取逗号分隔的数据,代码如下:
# -*- coding: utf-8 -*-
import os
import numpy as np
path = "wine/wine.txt"
data = np.loadtxt(path,dtype=float,delimiter=",")
print(data)
输出如下所示:
loadtxt()读入文件函数原型如下:
- loadtxt(fname, dtype, delimiter, converters, usecols)
其中参数fname表示文件路径,dtype表示数据类型,delimiter表示分隔符,converters将数据列与转换函数进行映射的字段,如{1:fun},usecols表示选取数据的列。
(3) 数据集拆分训练集和预测集
由于Wine数据集前59个样本全是第1类,中间71个样本为第2类,最后48个样本是第3类,所以需要将数据集拆分成训练集和预测集。步骤如下:
- 调用split()函数将数据集的第一列类标(Y数据)和13列特征(X数组)分隔开来。该函数参数包括data数据,分割位置,其中1表示从第一列分割,axis为1表示水平分割、0表示垂直分割。
- 由于数据集第一列存储的类标为1.0、2.0或3.0浮点型数据,需要将其转换为整型,这里在for循环中调用int()函数转换,存储至y数组中,也可采用np.astype()实现。
- 最后调用np.concatenate()函数将0-40、60-100、140-160行数据分割为训练集,包括13列特征和类标,其余78行数据为测试集。
代码如下:
# -*- coding: utf-8 -*-
import os
import numpy as np
path = "wine/wine.txt"
data = np.loadtxt(path,dtype=float,delimiter=",")
print(data)
yy, x = np.split(data, (1,), axis=1)
print(yy.shape, x.shape)
y = []
for n in yy:
y.append(int(n))
train_data = np.concatenate((x[0:40,:], x[60:100,:], x[140:160,:]), axis = 0) #训练集
train_target = np.concatenate((y[0:40], y[60:100], y[140:160]), axis = 0) #样本类别
test_data = np.concatenate((x[40:60, :], x[100:140, :], x[160:,:]), axis = 0) #测试集
test_target = np.concatenate((y[40:60], y[100:140], y[160:]), axis = 0) #样本类别
print(train_data.shape, train_target.shape)
print(test_data.shape, test_target.shape)
输出结果如下:
(178L, 1L)
(178L, 13L)
(100L, 1L) (100L, 13L)
(78L, 1L) (78L, 13L)
下面补充一种随机拆分的方式,调用 sklearn.model_selection.train_test_split 类随机划分训练集与测试集。代码如下:
from sklearn.model_selection import train_test_split
x, y = np.split(data, (1,), axis=1)
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1, train_size=0.7)
#Python2调用方法
#from sklearn.cross_validation import train_test_split
参数x表示所要划分的样本特征集;y是所要划分的样本结果;train_size表示训练样本占比,0.7表示将数据集划分为70%的训练集、30%的测试集;random_state是随机数的种子。该函数在部分版本的sklearn库中是导入model_selection类,建议读者下来尝试。
(4) KNN分类算法分析
上面已经将178个样本分成100个训练样本和78个测试样本,采用KNN分类算法训练模型,再对测试集进行预测,判别出测试样本所属于酒的类型,同时输出测试样本计算的正确率和错误率。KNN核心代码如下:
from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=3,algorithm='kd_tree')
clf.fit(train_data,train_target)
result = clf.predict(test_data)
print(result)
预测输出结果如下所示:
[1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 3 2 2 2 2 2 2 2 2 3 2 3 2 2 2 2
2 2 3 3 2 2 2 2 2 2 2 2 3 2 3 3 3 3 2 1 2 3 3 2 2 3 2 3 2 2 2 1 2 2 2 3 1
1 1 1 3]
(5) 完整代码
下面代码实现了调用Sklearn机器学习包中KNeighborsClassifier算法进行分类分析,并绘制预测的散点图和背景图,完整代码如下。
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-07-06
import os
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
#----------------------------------------------------------------------------
#第一步 加载数据集
path = "wine/wine.txt"
data = np.loadtxt(path,dtype=float,delimiter=",")
print(data)
#----------------------------------------------------------------------------
#第二步 划分数据集
yy, x = np.split(data, (1,), axis=1) #第一列为类标yy,后面13列特征为x
print(yy.shape, x.shape)
y = []
for n in yy: #将类标浮点型转化为整数
y.append(int(n))
x = x[:, :2] #获取x前两列数据,方便绘图 对应x、y轴
train_data = np.concatenate((x[0:40,:], x[60:100,:], x[140:160,:]), axis = 0) #训练集
train_target = np.concatenate((y[0:40], y[60:100], y[140:160]), axis = 0) #样本类别
test_data = np.concatenate((x[40:60, :], x[100:140, :], x[160:,:]), axis = 0) #测试集
test_target = np.concatenate((y[40:60], y[100:140], y[160:]), axis = 0) #样本类别
print(train_data.shape, train_target.shape)
print(test_data.shape, test_target.shape)
#----------------------------------------------------------------------------
#第三步 KNN训练
clf = KNeighborsClassifier(n_neighbors=3,algorithm='kd_tree') #K=3
clf.fit(train_data,train_target)
result = clf.predict(test_data)
print(result)
#----------------------------------------------------------------------------
#第四步 评价算法
print(sum(result==test_target)) #预测结果与真实结果比对
print(metrics.classification_report(test_target, result)) #准确率 召回率 F值
#----------------------------------------------------------------------------
#第五步 创建网格
x1_min, x1_max = test_data[:,0].min()-0.1, test_data[:,0].max()+0.1 #第一列
x2_min, x2_max = test_data[:,1].min()-0.1, test_data[:,1].max()+0.1 #第二列
xx, yy = np.meshgrid(np.arange(x1_min, x1_max, 0.1),
np.arange(x2_min, x2_max, 0.1)) #生成网格型数据
print(xx.shape, yy.shape) #(53L, 36L) (53L, 36L)
z = clf.predict(np.c_[xx.ravel(), yy.ravel()]) #ravel()拉直函数
print(xx.ravel().shape, yy.ravel().shape) #(1908L,) (1908L,)
print(np.c_[xx.ravel(), yy.ravel()].shape) #合并 (1908L,2)
#----------------------------------------------------------------------------
#第六步 绘图可视化
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF']) #颜色Map
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
plt.figure()
z = z.reshape(xx.shape)
print(xx.shape, yy.shape, z.shape, test_target.shape)
#(53L, 36L) (53L, 36L) (53L, 36L) (78L,)
plt.pcolormesh(xx, yy, z, cmap=cmap_light)
plt.scatter(test_data[:,0], test_data[:,1], c=test_target,
cmap=cmap_bold, s=50)
plt.show()
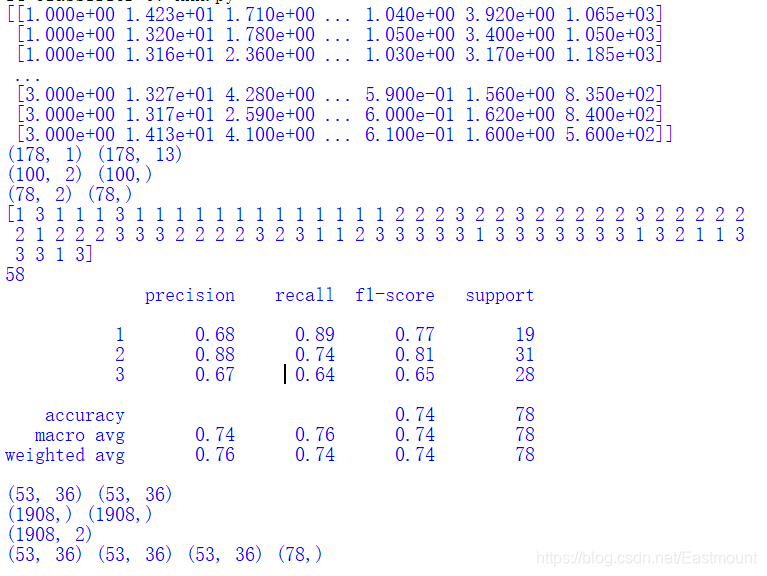
输出结果如下所示,包括预测的78行类标,共预测正确58行数据,准确率为0.76,召回率为0.74,f特征为0.74。其结果不太理想,需要进一步优化算法。
[1 3 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 3 2 2 3 2 2 2 2 2 3 2 2 2 2 2
2 1 2 2 2 3 3 3 2 2 2 2 3 2 3 1 1 2 3 3 3 3 3 1 3 3 3 3 3 3 3 1 3 2 1 1 3
3 3 1 3]
58
precision recall f1-score support
1 0.68 0.89 0.77 19
2 0.88 0.74 0.81 31
3 0.67 0.64 0.65 28
avg / total 0.76 0.74 0.74 78
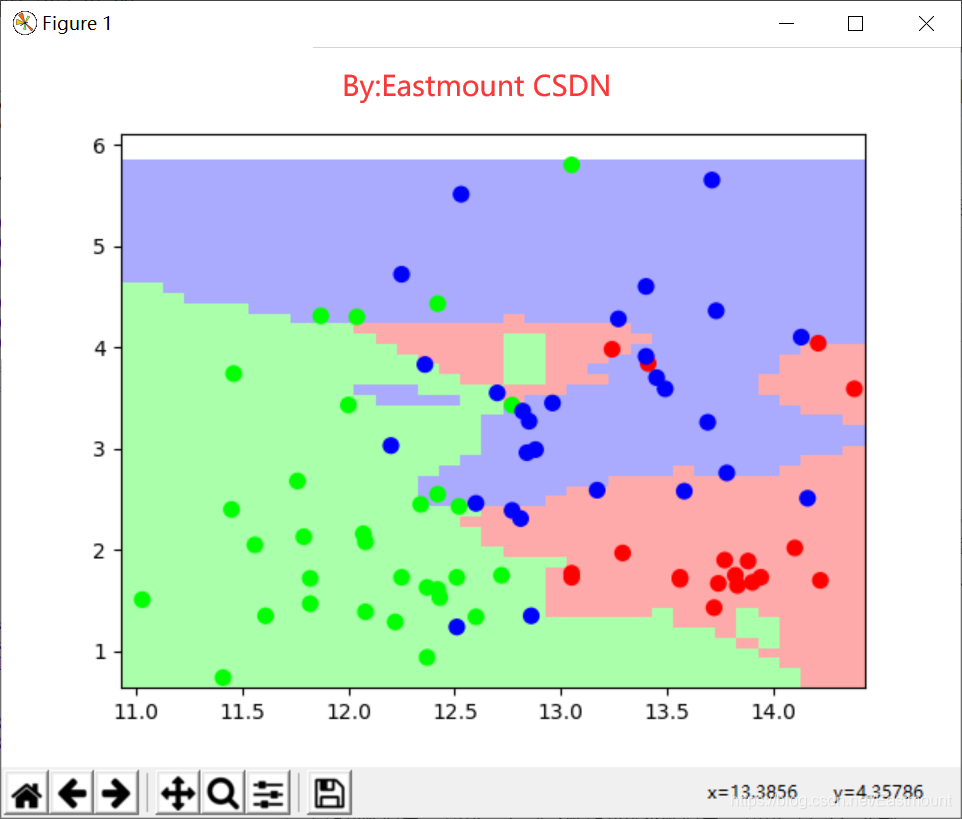
输出图形如图15所示,可以看到整个区域划分为三种颜色,左下角为绿色区域,右下角为红色区域,右上部分为蓝色区域。同时包括78个点分布,对应78行数据的类标,包括绿色、蓝色和红色的点。可以发现,相同颜色的点主要集中于该颜色区域,部分蓝色点划分至红色区域或绿色点划分至蓝色区域,则表示预测结果与实际结果不一致。
最后简单总结,整个分析过程包括六个步骤,大致内容如下:
- 1) 加载数据集
采用loadtxt()函数加载酒类数据集,采用逗号(,)分割。 - 2) 划分数据集
由于Wine数据集第一列为类标,后面13列为13个酒类特征,获取其中两列特征,并将其划分成特征数组和类标数组,调用concatenate()函数实现。 - 3) KNN训练
调用Sklearn机器学习包中KNeighborsClassifier()函数训练,设置K值为3类,并调用clf.fit(train_data,train_target)训练模型,clf.predict(test_data)预测分类结果。 - 4) 评价算法
通过classification_report()函数计算该分类预测结果的准确率、召回率和F值。 - 5) 创建网格
由于绘图中,拟将预测的类标划分为三个颜色区域,真实的分类结果以散点图形式呈现,故需要获取数据集中两列特征的最大值和最小值,并创建对应的矩阵网格,调用numpy扩展包的meshgrid()函数实现,在对其颜色进行预测。 - 6) 绘图可视化
设置不同类标的颜色,调用pcolormesh()函数绘制背景区域颜色,调用scatter()函数绘制实际结果的散点图,形成如图15的效果图。
支持向量机(Support Vector Machine,简称SVM)是常见的一种判别方法。在机器学习领域,是一个有监督的学习模型,通常用来进行模式识别、分类以及回归分析。该算法的最大特点是根据结构风险最小化准则,以最大化分类间隔构造最优分类超平面来提高学习机的泛化能力,较好地解决了非线性、高维数、局部极小点等问题。
(1) 基础概念
由于作者数学推算能力不太好,同时SVM原理也比较复杂,所以SVM算法基础知识推荐大家阅读CSDN博客著名算法大神“JULY”的文章《支持向量机通俗导论(理解SVM的三层境界)》,这篇文章由浅入深的讲解了SVM算法,而本小节作者主要讲解SVM的用法。
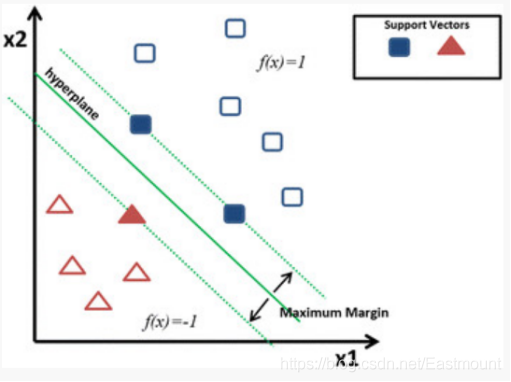
SVM分类算法的核心思想是通过建立某种核函数,将数据在高维寻找一个满足分类要求的超平面,使训练集中的点距离分类面尽可能的远,即寻找一个分类面使得其两侧的空白区域最大。如图19.16所示,两类样本中离分类面最近的点且平行于最优分类面的超平面上的训练样本就叫做支持向量。
(2) SVM导入方法
SVM分类算法在Sklearn机器学习包中,实现的类是 svm.SVC,即C-Support Vector Classification,它是基于libsvm实现的。构造方法如下:
SVC(C=1.0,
cache_size=200,
class_weight=None,
coef0=0.0,
decision_function_shape=None,
degree=3,
gamma='auto',
kernel='rbf',
max_iter=-1,
probability=False,
random_state=None,
shrinking=True,
tol=0.001,
verbose=False)
其中参数含义如下:
- C表示目标函数的惩罚系数,用来平衡分类间隔margin和错分样本的,默认值为1.0;
- cache_size是制定训练所需要的内存(以MB为单位);
- gamma是核函数的系数,默认是gamma=1/n_features;
- kernel可以选择RBF、Linear、Poly、Sigmoid,默认的是RBF;
- degree决定了多项式的最高次幂;
- max_iter表示最大迭代次数,默认值为1;
- coef0是核函数中的独立项;
- class_weight表示每个类所占据的权重,不同的类设置不同的惩罚参数C,缺省为自适应;
- decision_function_shape包括ovo(一对一)、ovr(多对多)或None(默认值)。
SVC算法主要包括两个步骤:
- 训练:
nbrs.fit(data, target) - 预测:
pre = clf.predict(data)
下面这段代码是简单调用SVC分类算法进行预测的例子,数据集中x和y坐标为负数的类标为1,x和y坐标为正数的类标为2,同时预测点[-0.8,-1]的类标为1,点[2,1]的类标为2。
import numpy as np
from sklearn.svm import SVC
X = np.array([[-1, -1], [-2, -2], [1, 3], [4, 6]])
y = np.array([1, 1, 2, 2])
clf = SVC()
clf.fit(X, y)
print(clf)
print(clf.predict([[-0.8,-1], [2,1]]))
#输出结果:[1, 2]
支持向量机分类器还有其他的方法,比如NuSVC核支持向量分类,LinearSVC线性向量支持分类等,这里不再介绍。同时,支持向量机也已经推广到解决回归问题,称为支持向量回归,比如SVR做线性回归。
接着采用SVM分类算法对酒类数据集Wine进行分析,并对比前面19.3小节的实例代码,校验SVM分类算法和KNN分类算法的分析结果和可视化分析的优劣。其分析步骤基本一致,主要包括如下六个步骤:
- 第一步,加载数据集。采用loadtxt()函数加载酒类数据集,采用逗号(,)分割。
- 第二步,划分数据集。将Wine数据集划分为训练集和预测集,仅提取酒类13个特种中的两列特征进行数据分析。
- 第三步,SVM训练。导入Sklearn机器学习包中svm.SVC()函数分析,调用fit()函数训练模型,predict(test_data)函数预测分类结果。
- 第四步,评价算法。通过classification_report()函数计算该分类预测结果的准确率、召回率和F值。
- 第五步,创建网格。获取数据集中两列特征的最大值和最小值,并创建对应的矩阵网格,用于绘制背景图,调用numpy扩展包的meshgrid()函数实现。
- 第六步,绘图可视化。设置不同类标的颜色,调用pcolormesh()函数绘制背景区域颜色,调用scatter()函数绘制实际结果的散点图。
完整代码如下所示:
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-07-06
import os
import numpy as np
from sklearn.svm import SVC
from sklearn import metrics
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
#----------------------------------------------------------------------------
#第一步 加载数据集
path = "wine/wine.txt"
data = np.loadtxt(path,dtype=float,delimiter=",")
print(data)
#----------------------------------------------------------------------------
#第二步 划分数据集
yy, x = np.split(data, (1,), axis=1) #第一列为类标yy,后面13列特征为x
print(yy.shape, x.shape)
y = []
for n in yy: #将类标浮点型转化为整数
y.append(int(n))
x = x[:, :2] #获取x前两列数据,方便绘图 对应x、y轴
train_data = np.concatenate((x[0:40,:], x[60:100,:], x[140:160,:]), axis = 0) #训练集
train_target = np.concatenate((y[0:40], y[60:100], y[140:160]), axis = 0) #样本类别
test_data = np.concatenate((x[40:60, :], x[100:140, :], x[160:,:]), axis = 0) #测试集
test_target = np.concatenate((y[40:60], y[100:140], y[160:]), axis = 0) #样本类别
print(train_data.shape, train_target.shape)
print(test_data.shape, test_target.shape)
#----------------------------------------------------------------------------
#第三步 SVC训练
clf = SVC()
clf.fit(train_data,train_target)
result = clf.predict(test_data)
print(result)
#----------------------------------------------------------------------------
#第四步 评价算法
print(sum(result==test_target)) #预测结果与真实结果比对
print(metrics.classification_report(test_target, result)) #准确率 召回率 F值
#----------------------------------------------------------------------------
#第五步 创建网格
x1_min, x1_max = test_data[:,0].min()-0.1, test_data[:,0].max()+0.1 #第一列
x2_min, x2_max = test_data[:,1].min()-0.1, test_data[:,1].max()+0.1 #第二列
xx, yy = np.meshgrid(np.arange(x1_min, x1_max, 0.1),
np.arange(x2_min, x2_max, 0.1)) #生成网格型数据
z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
#----------------------------------------------------------------------------
#第六步 绘图可视化
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF']) #颜色Map
cmap_bold = ListedColormap(['#000000', '#00FF00', '#FFFFFF'])
plt.figure()
z = z.reshape(xx.shape)
print(xx.shape, yy.shape, z.shape, test_target.shape)
plt.pcolormesh(xx, yy, z, cmap=cmap_light)
plt.scatter(test_data[:,0], test_data[:,1], c=test_target,
cmap=cmap_bold, s=50)
plt.show()
代码提取了178行数据的第一列作为类标,剩余13列数据作为13个特征的数据集,并划分为训练集(100行)和测试集(78行)。输出结果如下,包括78行SVM分类预测的类标结果,其中61行数据类标与真实的结果一致,其准确率为0.78,召回率为0.78,F1特征为0.78。
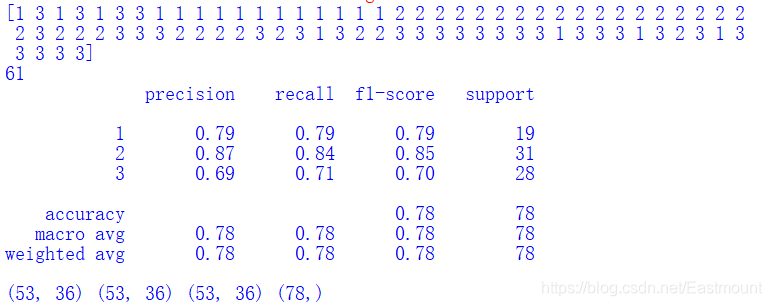
最后可视化绘图输出如下图所示的结果。

前面SVM分析红酒数据集的代码存在两个缺点,一是采用固定的组合方式划分的数据集,即调用np.concatenate()函数将0-40、60-100、140-160行数据分割为训练集,其余为预测集;二是只提取了数据集中的两列特征进行SVM分析和可视化绘图,即调用“x = x[:, :2]”获取前两列特征,而红酒数据集共有13列特征。
真实的数据分析中通常会随机划分数据集,分析过程也是对所有的特征进行训练及预测操作,再经过降维处理之后进行可视化绘图展示。下面对SVM分析红酒数据集实例进行简单的代码优化,主要包括:
- 随机划分红酒数据集
- 对数据集的所有特征进行训练和预测分析
- 采用PCA算法降维后再进行可视化绘图操作
完整代码如下,希望读者也认真学习该部分知识,更好地优化自己的研究或课题。
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-07-06
import os
import numpy as np
from sklearn.svm import SVC
from sklearn import metrics
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
#第一步 加载数据集
path = "wine/wine.txt"
data = np.loadtxt(path,dtype=float,delimiter=",")
print(data)
#第二步 划分数据集
yy, x = np.split(data, (1,), axis=1) #第一列类标yy,后面13列特征为x
print(yy.shape, x.shape)
y = []
for n in yy:
y.append(int(n))
y = np.array(y, dtype = int) #list转换数组
#划分数据集 测试集40%
train_data, test_data, train_target, test_target = train_test_split(x, y, test_size=0.4, random_state=42)
print(train_data.shape, train_target.shape)
print(test_data.shape, test_target.shape)
#第三步 SVC训练
clf = SVC()
clf.fit(train_data, train_target)
result = clf.predict(test_data)
print(result)
print(test_target)
#第四步 评价算法
print(sum(result==test_target)) #预测结果与真实结果比对
print(metrics.classification_report(test_target, result)) #准确率 召回率 F值
#第五步 降维操作
pca = PCA(n_components=2)
newData = pca.fit_transform(test_data)
#第六步 绘图可视化
plt.figure()
cmap_bold = ListedColormap(['#000000', '#00FF00', '#FFFFFF'])
plt.scatter(newData[:,0], newData[:,1], c=test_target, cmap=cmap_bold, s=50)
plt.show()
输出结果如下所示,其准确率、召回率和F值很低,仅为50%、39%和23%。
(106L, 13L) (106L,)
(72L, 13L) (72L,)
[2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
[1 1 3 1 2 1 2 3 2 3 1 3 1 2 1 2 2 2 1 2 1 2 2 3 3 3 2 2 2 1 1 2 3 1 1 1 3
3 2 3 1 2 2 2 3 1 2 2 3 1 2 1 1 3 3 2 2 1 2 1 3 2 2 3 1 1 1 3 1 1 2 3]
28
precision recall f1-score support
1 1.00 0.04 0.07 26
2 0.38 1.00 0.55 27
3 0.00 0.00 0.00 19
avg / total 0.50 0.39 0.23 72
上述代码如下采用决策树进行分析,则其准确率、召回率和F值就很高,结果如下所示。所以并不是每种分析算法都适应所有的数据集,不同数据集其特征不同,最佳分析的算也会不同,我们在进行数据分析时,通常会对比多种分析算法,再优化自己的实验和模型。
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()
print(metrics.classification_report(test_target, result))
# precision recall f1-score support
#
# 1 0.96 0.88 0.92 26
# 2 0.90 1.00 0.95 27
# 3 1.00 0.95 0.97 19
#
#avg / total 0.95 0.94 0.94 72
SVM算法分析后输出的图形如下所示。
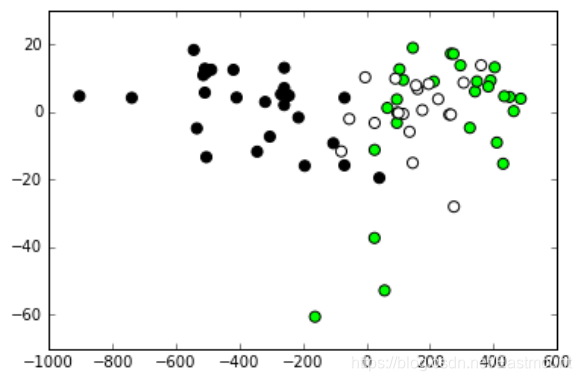
算法评价和对比实验是深度学习重要的知识点,这里作者对各种机器学习分类算法进行对比,以鸢尾花数据集为例,我们从绘制的分类边界效果以及实验评估指标(Precision、Recall、F1-socre)分别进行对比。参考文章如下,推荐大家学习:
原始代码如下:
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-07-06
# 该部分参考知乎萌弟老师:https://zhuanlan.zhihu.com/p/173945775
import numpy as np
from sklearn import metrics
from sklearn import datasets
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
#------------------------------------------------------------------------
#第一步 导入数据
iris = datasets.load_iris()
X = iris.data[:,[2,3]]
y = iris.target
print("Class labels:",np.unique(y)) #打印分类类别的种类 [0 1 2]
#30%测试数据 70%训练数据 stratify=y表示训练数据和测试数据具有相同的类别比例
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=1,stratify=y)
#------------------------------------------------------------------------
#第二步 数据标准化
sc = StandardScaler() #估算训练数据中的mu和sigma
sc.fit(X_train) #使用训练数据中的mu和sigma对数据进行标准化
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
print(X_train_std)
print(X_test_std)
#------------------------------------------------------------------------
#第三步 可视化函数 画出决策边界
def plot_decision_region(X,y,classifier,resolution=0.02):
markers = ('s','x','o','^','v')
colors = ('red','blue','lightgreen','gray','cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min,x1_max = X[:,0].min()-1,X[:,0].max()+1
x2_min,x2_max = X[:,1].min()-1,X[:,1].max()+1
xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),
np.arange(x2_min,x2_max,resolution))
Z = classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1,xx2,Z,alpha=0.3,cmap=cmap)
plt.xlim(xx1.min(),xx1.max())
plt.ylim(xx2.min(),xx2.max())
# plot class samples
for idx,cl in enumerate(np.unique(y)):
plt.scatter(x=X[y==cl,0],
y = X[y==cl,1],
alpha=0.8,
c=colors[idx],
marker = markers[idx],
label=cl,
edgecolors='black')
#------------------------------------------------------------------------
#第四步 决策树分类
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(criterion='gini',max_depth=4,random_state=1)
tree.fit(X_train_std,y_train)
print(X_train_std.shape, X_test_std.shape, len(y_train), len(y_test)) #(105, 2) (45, 2) 105 45
res1 = tree.predict(X_test_std)
print(res1)
print(metrics.classification_report(y_test, res1, digits=4)) #四位小数
plot_decision_region(X_train_std,y_train,classifier=tree,resolution=0.02)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.title('DecisionTreeClassifier')
plt.legend(loc='upper left')
plt.show()
实验的精确率、召回率和F1值输出如下:
- macro avg: 0.9792 0.9778 0.9778
precision recall f1-score support
0 1.0000 1.0000 1.0000 15
1 0.9375 1.0000 0.9677 15
2 1.0000 0.9333 0.9655 15
accuracy 0.9778 45
macro avg 0.9792 0.9778 0.9778 45
weighted avg 0.9792 0.9778 0.9778 45
绘制的训练数据分类效果如下图所示,可以看到分类效果明显。
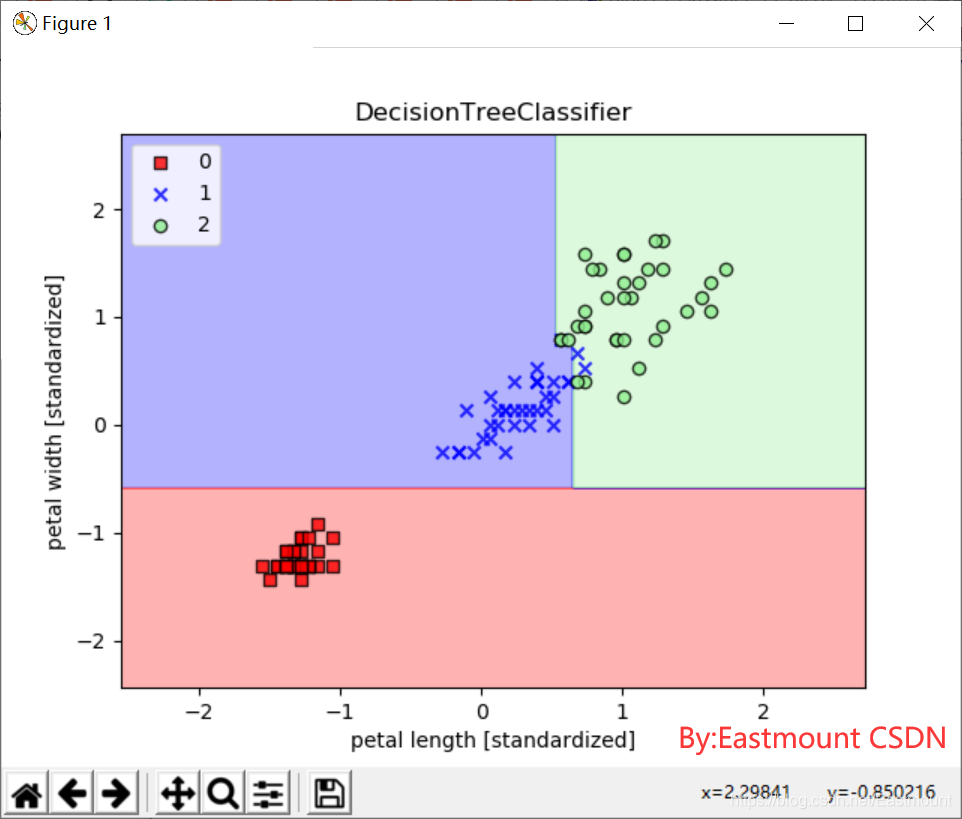
核心代码如下:
- macro avg: 0.98 0.98 0.98
#第五步 KNN分类
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=2,p=2,metric="minkowski")
knn.fit(X_train_std,y_train)
res2 = knn.predict(X_test_std)
print(res2)
print(metrics.classification_report(y_test, res2, digits=4)) #四位小数
plot_decision_region(X_train_std,y_train,classifier=knn,resolution=0.02)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.title('KNeighborsClassifier')
plt.legend(loc='upper left')
plt.show()
输出结果如下:
- macro avg: 0.9792 0.9778 0.9778
precision recall f1-score support
0 1.0000 1.0000 1.0000 15
1 0.9375 1.0000 0.9677 15
2 1.0000 0.9333 0.9655 15
accuracy 0.9778 45
macro avg 0.9792 0.9778 0.9778 45
weighted avg 0.9792 0.9778 0.9778 45
绘制的训练数据分类效果如下图所示:
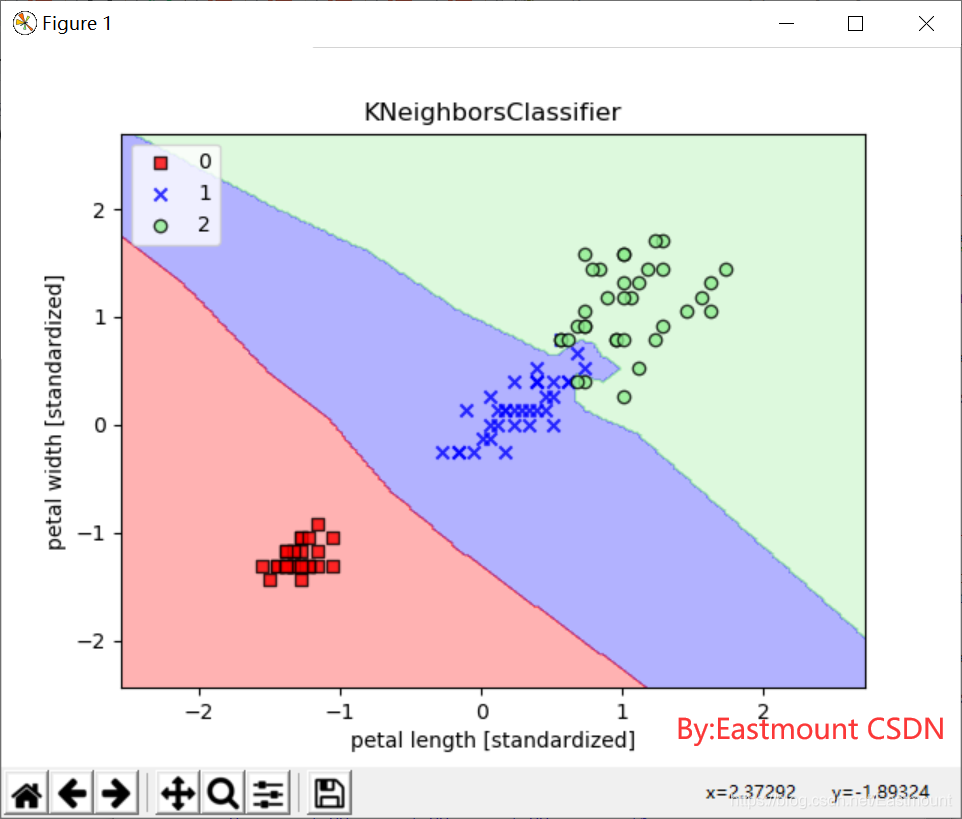
核心代码如下:
#第六步 SVM分类 核函数对非线性分类问题建模(gamma=0.20)
from sklearn.svm import SVC
svm = SVC(kernel='rbf',random_state=1,gamma=0.20,C=1.0) #较小的gamma有较松的决策边界
svm.fit(X_train_std,y_train)
res3 = svm.predict(X_test_std)
print(res3)
print(metrics.classification_report(y_test, res3, digits=4))
plot_decision_region(X_train_std,y_train,classifier=svm,resolution=0.02)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.title('SVM')
plt.legend(loc='upper left')
plt.show()
输出结果如下:
- macro avg: 0.9361 0.9333 0.9340
precision recall f1-score support
0 1.0000 0.9333 0.9655 15
1 0.9333 0.9333 0.9333 15
2 0.8750 0.9333 0.9032 15
accuracy 0.9333 45
macro avg 0.9361 0.9333 0.9340 45
weighted avg 0.9361 0.9333 0.9340 45
绘制的训练数据分类效果如下图所示:
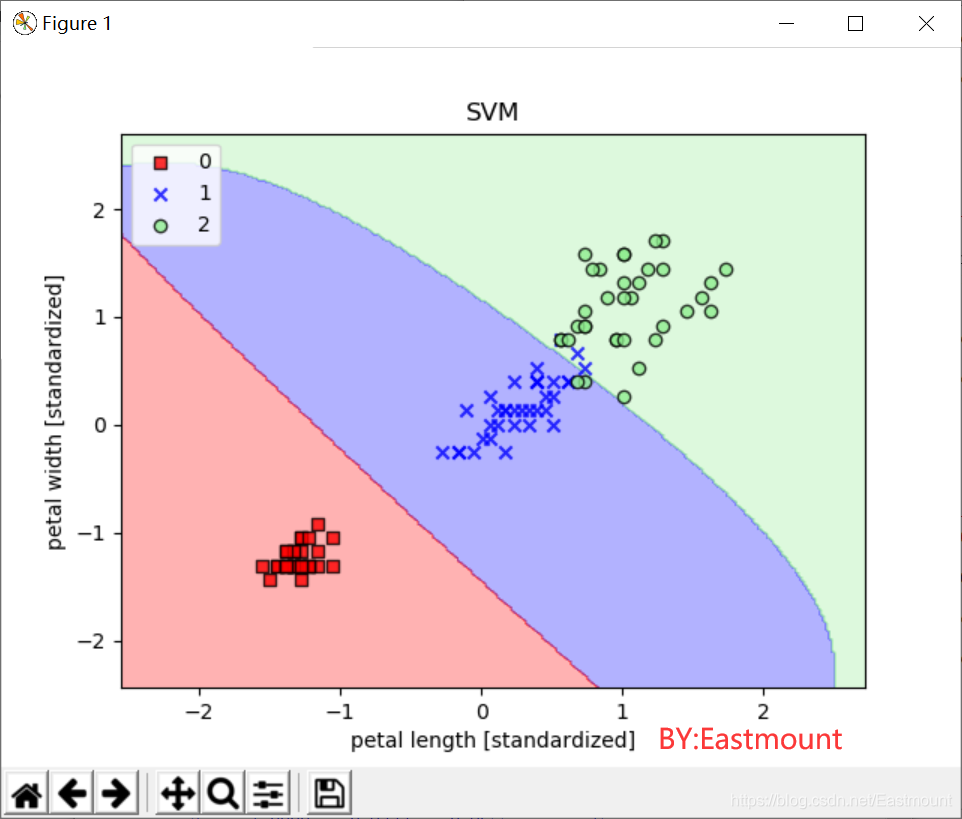
如果使用的核函数gamma为100,然后实现非线性分类,则绘制结果如下图所示:
- svm = SVC(kernel=‘rbf’,random_state=1,gamma=100.0,C=1.0,verbose=1)
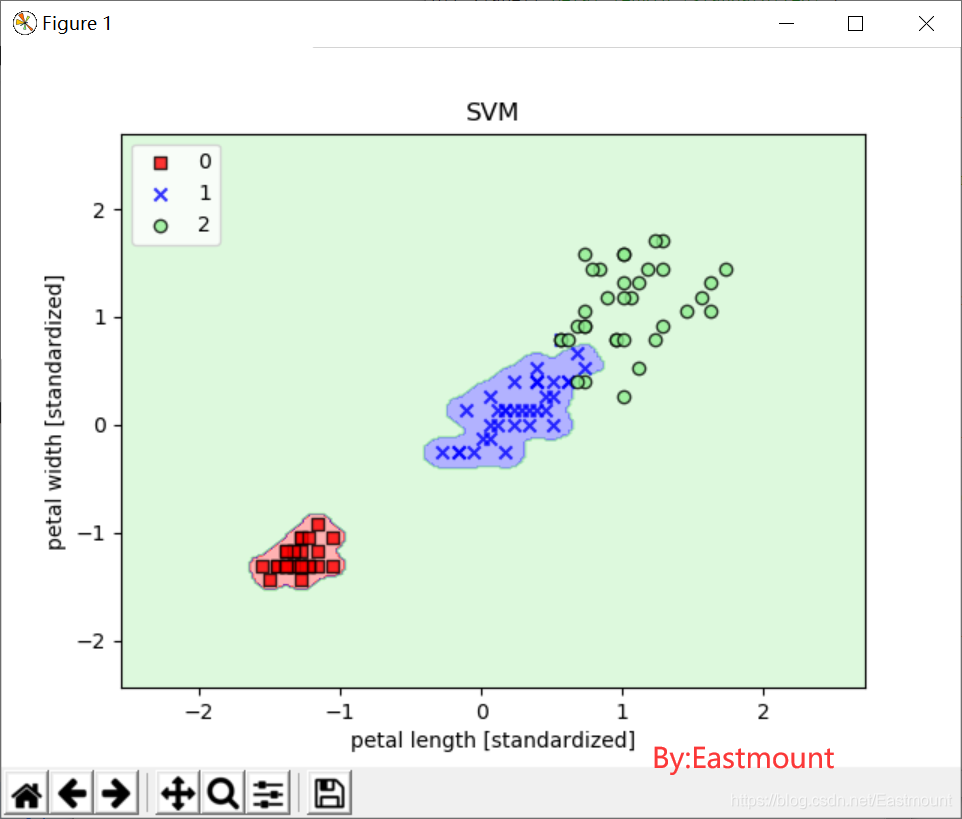
引用萌弟老师的结论,非常土建大家去关注他。
从不同的gamma取值的图像来看:对于高斯核函数,增大gamma值,将增大训练样本的影响范围,导致决策边界紧缩和波动;较小的gamma值得到的决策边界相对宽松。虽然较大的gamma值在训练样本中有很小的训练误差,但是很可能泛化能力较差,容易出现过拟合。
核心代码如下:
#第七步 逻辑回归分类
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C=100.0,random_state=1)
lr.fit(X_train_std,y_train)
res4 = lr.predict(X_test_std)
print(res4)
print(metrics.classification_report(y_test, res4, digits=4))
plot_decision_region(X_train_std,y_train,classifier=lr,resolution=0.02)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.title('LogisticRegression')
plt.legend(loc='upper left')
plt.show()
输出结果如下:
- macro avg: 0.9792 0.9778 0.9778
precision recall f1-score support
0 1.0000 1.0000 1.0000 15
1 0.9375 1.0000 0.9677 15
2 1.0000 0.9333 0.9655 15
accuracy 0.9778 45
macro avg 0.9792 0.9778 0.9778 45
weighted avg 0.9792 0.9778 0.9778 45
绘制的训练数据分类效果如下图所示:
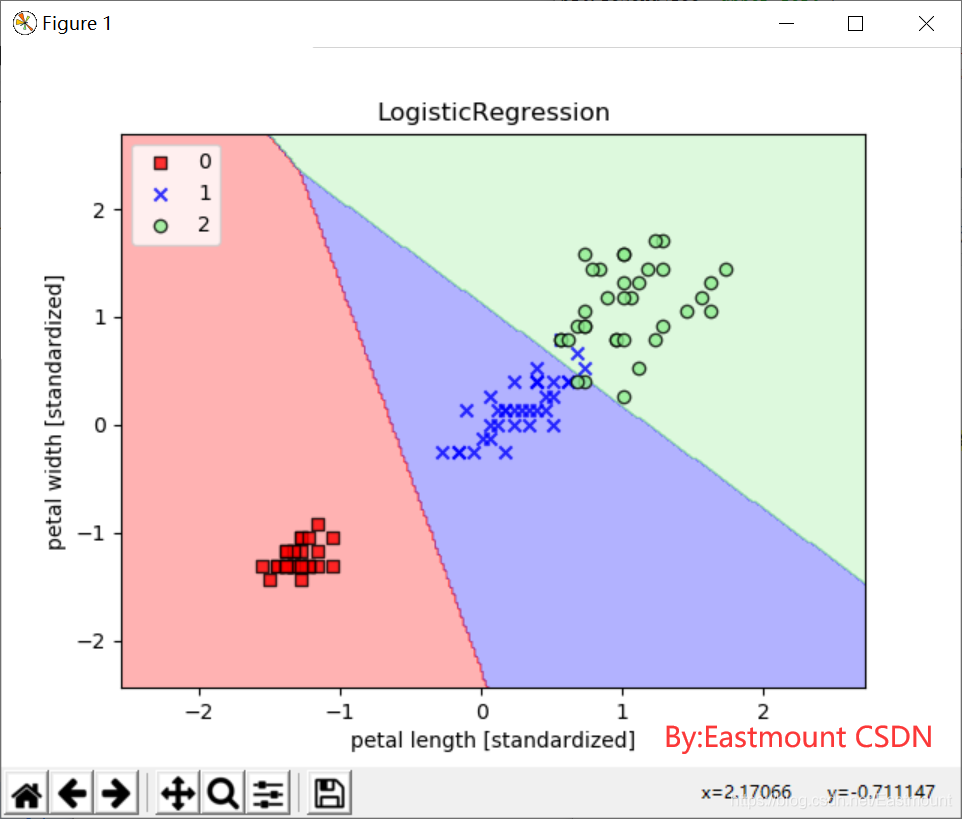
核心代码如下:
#第八步 朴素贝叶斯分类
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
gnb.fit(X_train_std,y_train)
res5 = gnb.predict(X_test_std)
print(res5)
print(metrics.classification_report(y_test, res5, digits=4))
plot_decision_region(X_train_std,y_train,classifier=gnb,resolution=0.02)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.title('GaussianNB')
plt.legend(loc='upper left')
plt.show()
输出结果如下:
- macro avg: 0.9792 0.9778 0.9778
precision recall f1-score support
0 1.0000 1.0000 1.0000 15
1 0.9375 1.0000 0.9677 15
2 1.0000 0.9333 0.9655 15
accuracy 0.9778 45
macro avg 0.9792 0.9778 0.9778 45
weighted avg 0.9792 0.9778 0.9778 45
绘制的训练数据分类效果如下图所示,还挺好看的,边界呈曲线分布。
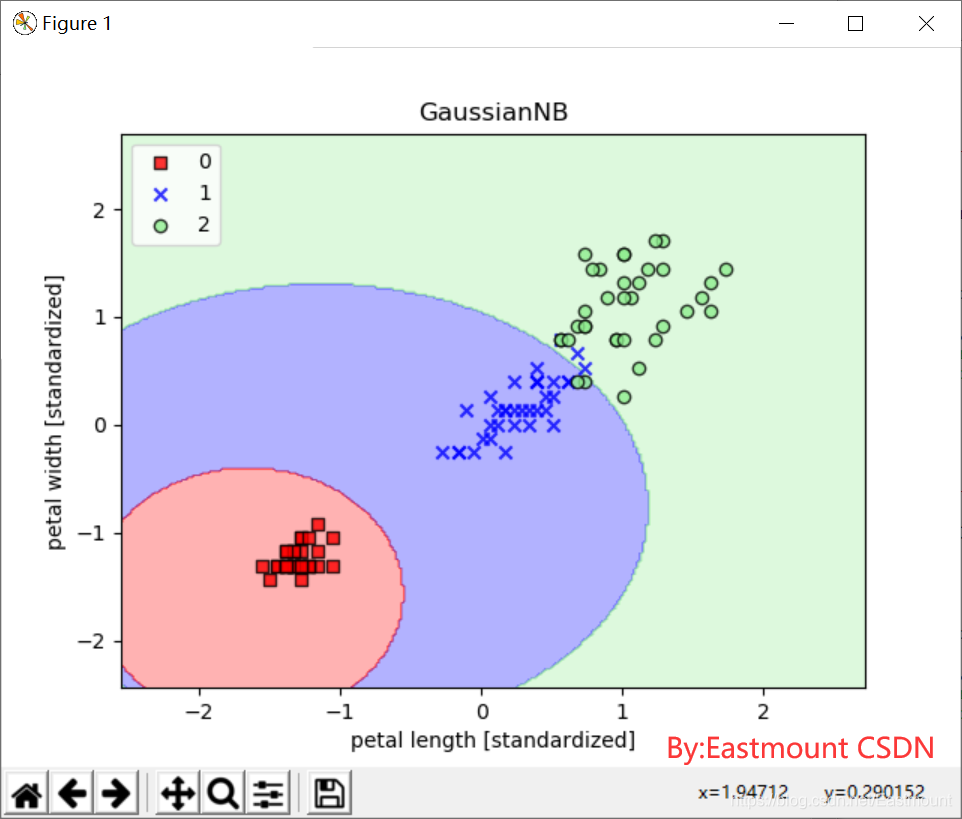
核心代码如下:
#第九步 随机森林分类
from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier(criterion='gini',
n_estimators=25,
random_state=1,
n_jobs=2,
verbose=1)
forest.fit(X_train_std,y_train)
res6 = gnb.predict(X_test_std)
print(res6)
print(metrics.classification_report(y_test, res6, digits=4))
plot_decision_region(X_train_std,y_train,classifier=forest,resolution=0.02)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.title('GaussianNB')
plt.legend(loc='upper left')
plt.show()
输出结果如下:
- macro avg: 0.9792 0.9778 0.9778
precision recall f1-score support
0 1.0000 1.0000 1.0000 15
1 0.9375 1.0000 0.9677 15
2 1.0000 0.9333 0.9655 15
accuracy 0.9778 45
macro avg 0.9792 0.9778 0.9778 45
weighted avg 0.9792 0.9778 0.9778 45
绘制的训练数据分类效果如下图所示:
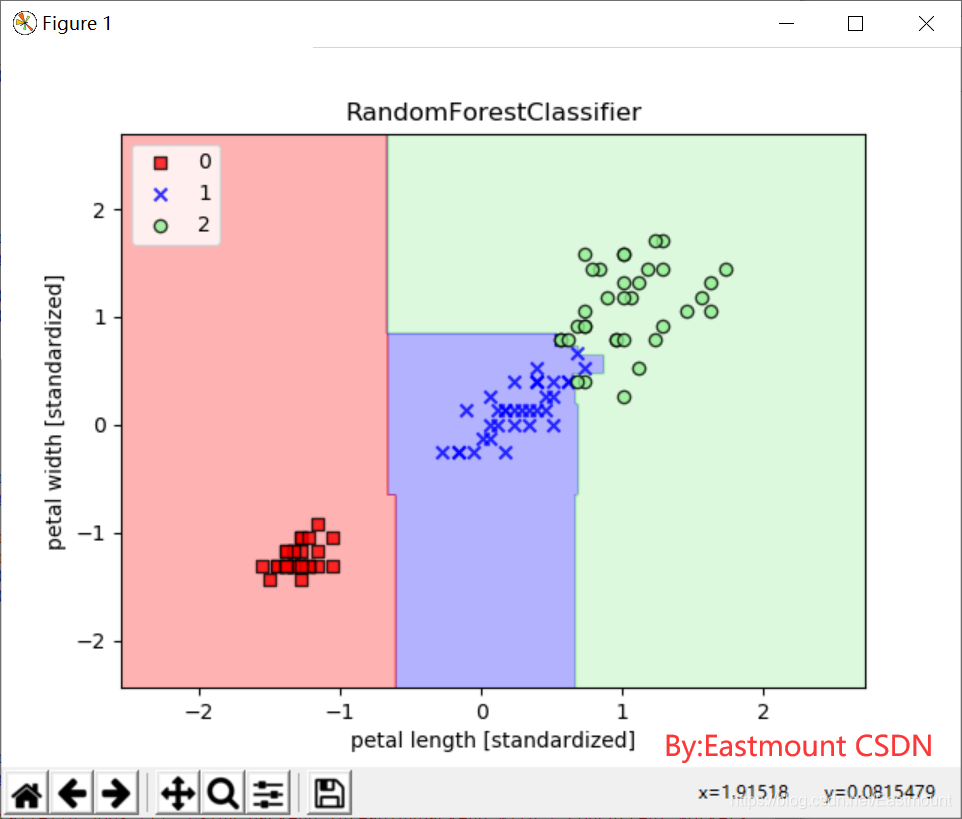
核心代码如下:
#第十步 集成学习分类
from sklearn.ensemble import AdaBoostClassifier
ada = AdaBoostClassifier()
ada.fit(X_train_std,y_train)
res7 = ada.predict(X_test_std)
print(res7)
print(metrics.classification_report(y_test, res7, digits=4))
plot_decision_region(X_train_std,y_train,classifier=forest,resolution=0.02)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.title('AdaBoostClassifier')
plt.legend(loc='upper left')
plt.show()
输出结果如下:
- macro avg: 0.9792 0.9778 0.9778
precision recall f1-score support
0 1.0000 1.0000 1.0000 15
1 0.9375 1.0000 0.9677 15
2 1.0000 0.9333 0.9655 15
accuracy 0.9778 45
macro avg 0.9792 0.9778 0.9778 45
weighted avg 0.9792 0.9778 0.9778 45
绘制的训练数据分类效果如下图所示:

核心代码如下:
#第11步 GradientBoosting分类
from sklearn.ensemble import GradientBoostingClassifier
gb = GradientBoostingClassifier()
ada.fit(X_train_std,y_train)
res8 = ada.predict(X_test_std)
print(res8)
print(metrics.classification_report(y_test, res8, digits=4))
plot_decision_region(X_train_std,y_train,classifier=forest,resolution=0.02)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.title('GradientBoostingClassifier')
plt.legend(loc='upper left')
plt.show()
输出结果如下:
- macro avg: 0.9792 0.9778 0.9778
precision recall f1-score support
0 1.0000 1.0000 1.0000 15
1 0.9375 1.0000 0.9677 15
2 1.0000 0.9333 0.9655 15
accuracy 0.9778 45
macro avg 0.9792 0.9778 0.9778 45
weighted avg 0.9792 0.9778 0.9778 45
绘制的训练数据分类效果如下图所示:
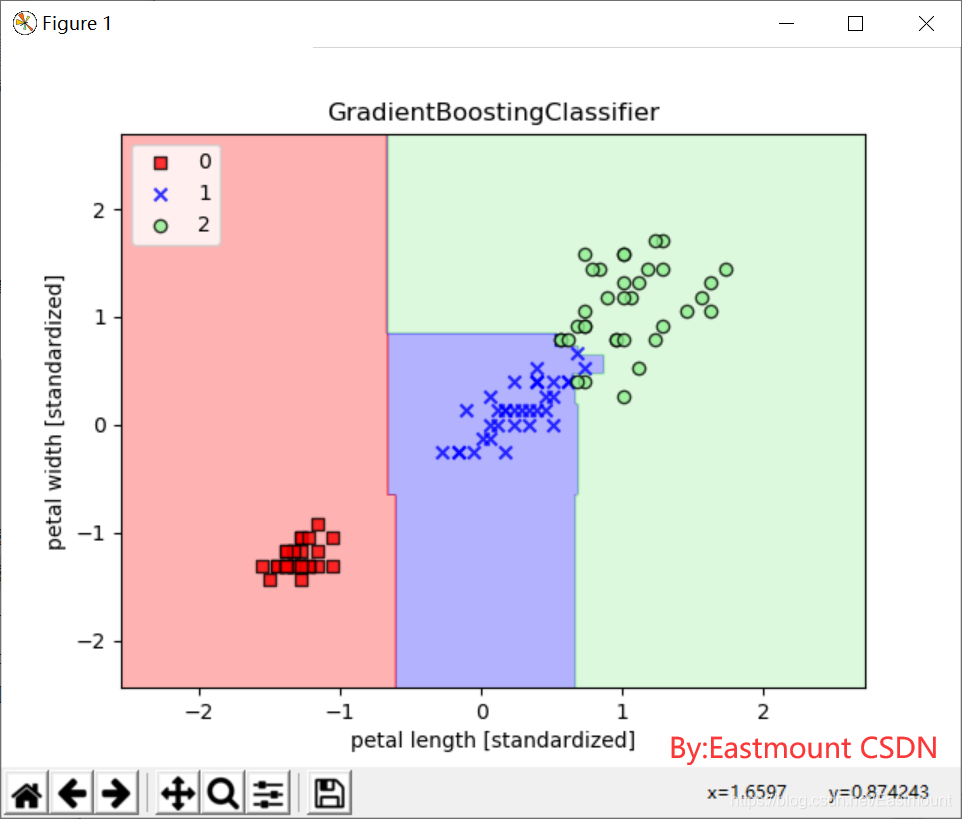
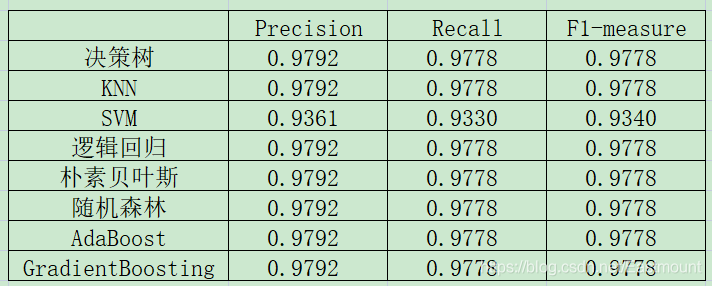
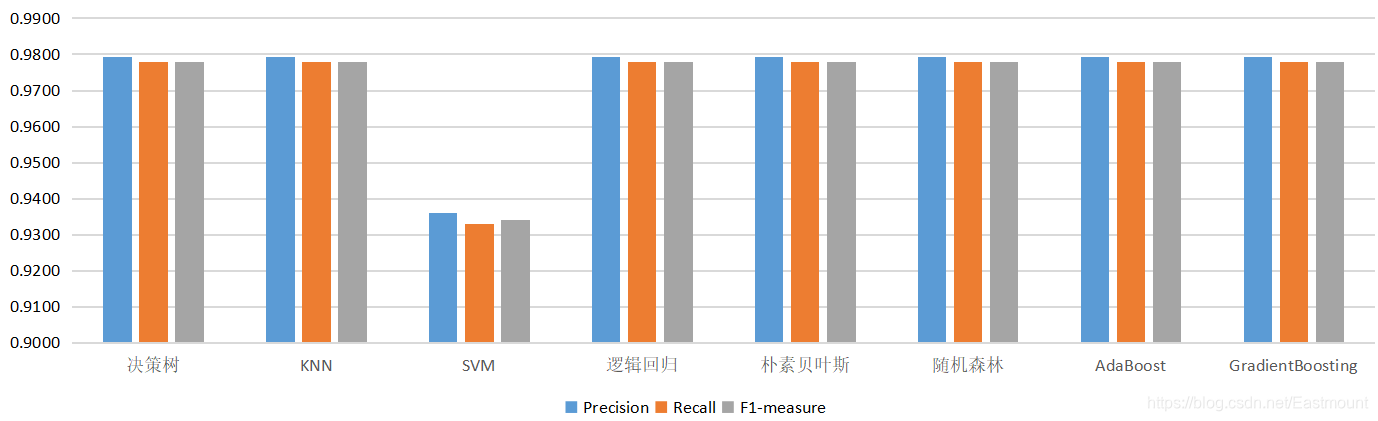
最后通常需要对实验结果进行对比,由于数据集比较少,所有效果都比较好,这里不太好进行对比实验。简单给出两张对比结果图,但方法是类似的。随着作者深入会分享更多相关文章。
写到这里,这篇文章就结束了,您是否对分类更好的认识呢?
聚类是通过定义一种距离度量方法,表示两个东西的相似程度,然后将类内相似度高且类间相似度低的数据放在一个类中,它是不需要标注结果的无监督学习算法。与之不同,分类是需要标注类标的,属于有监督学习,它表示收集某一类数据的共有特征,找出区分度大的特征,用这些特征对要分类的数据进行分类,并且由于是标注结果的,可以通过反复地训练来提升分类算法。
常见的分类算法包括朴素贝叶斯、逻辑回归、决策树、支持向量机等。常见应用比如通过分析市民历史公交卡交易数据来分类预测乘客的出行习惯和偏好;京东从海量商品图片中提取图像特征,通过分类给用户推荐商品和广告,比如“找同款”应用;基于短信文本内容的分类智能化识别垃圾短信及其变种,防止骚扰手机用户;搜索引擎通过训练用户的历史查询词和用户属性标签(如性别、年龄、爱好),构建分类算法来预测新增用户的属性及偏好等。不同的分类算法有不同的优劣,希望读者下来编写代码体会不同的分类算法的特点。
最后希望读者能复现每一行代码,只有实践才能进步。同时更多聚类算法和原理知识,希望读者下来自行深入学习研究,也推荐大家结合Sklearn官网和开源网站学习更多的机器学习知识。
该系列所有代码下载地址:
感谢在求学路上的同行者,不负遇见,勿忘初心。这周的留言感慨~
感恩能与大家在华为云遇见!
希望能与大家一起在华为云社区共同成长,原文地址:https://blog.csdn.net/Eastmount/article/details/118524484
【百变AI秀】有奖征文火热进行中:https://bbs.huaweicloud.com/blogs/29670
(By:娜璋之家 Eastmount 2021-08-31 夜于贵阳)
参考文献:
- [1] 杨秀璋. 专栏:知识图谱、web数据挖掘及NLP - CSDN博客[EB/OL]. (2016-09-19)[2017-11-07]. http://blog.csdn.net/column/details/eastmount-kgdmnlp.html.
- [2] 张良均,王路,谭立云,苏剑林. Python数据分析与挖掘实战[M]. 北京:机械工业出版社,2016.
- [3] (美)Wes McKinney著. 唐学韬等译. 利用Python进行数据分析[M]. 北京:机械工业出版社,2013.
- [4] Jiawei Han,Micheline Kamber著. 范明,孟小峰译. 数据挖掘概念与技术. 北京:机械工业出版社,2007.
- [5] 杨秀璋. [Python数据挖掘课程] 四.决策树DTC数据分析及鸢尾数据集分析[EB/OL].(2016-10-15)[2017-11-26]. http://blog.csdn.net/eastmount/article/details/52820400.
- [6] 杨秀璋. [Python数据挖掘课程] 五.线性回归知识及预测糖尿病实例[EB\OL]. (2016-10-28)[2017-11-26]. http://blog.csdn.net/eastmount/article/details/52929765.
- [7] jackywu1010. 分类算法概述与比较[EB/OL]. (2011-12-09)[2017-11-26]. http://blog.csdn.net/jackywu1010/article/details/7055561.
- [8] 百度百科. 邻近算法[EB/OL]. (2015-09-16)[2017-11-26]. https://baike.baidu.com/item/邻近算法/1151153?fr=aladdin.
- [9] 杨秀璋. [python数据挖掘课程] 十九.鸢尾花数据集可视化、线性回归、决策树花样分析[EB/OL]. (2017-12-02)[2017-12-02]. http://blog.csdn.net/eastmount/article/
details/78692227. - [10]杨秀璋. [python数据挖掘课程] 二十.KNN最近邻分类算法分析详解及平衡秤TXT数据集读取[EB/OL]. (2017-12-08)[2017-12-08]. http://blog.csdn.net/eastmount/article/
details/78747128. - [11] lsldd. 用Python开始机器学习(4:KNN分类算法)[EB/OL]. (2014-11-23)[2017-11-26]. http://blog.csdn.net/lsldd/article/details/41357931.
- [12] UCI官网. UCI Machine Learning Repository: Wine Data Set[EB/OL]. (2017)[2017-12-08]. http://archive.ics.uci.edu/ml/datasets/Wine.
- [13]杨秀璋. [python数据挖掘课程] 二十一.朴素贝叶斯分类器详解及中文文本舆情分析[EB/OL]. (2018-01-24)[2018-01-24]. http://blog.csdn.net/eastmount/article/
details/79128235. - [14] scikit-learn官网. Nearest Neighbors Classification scikit-learn[EB\OL]. (2017)[2017-12-08]. http://scikit-learn.org/stable/auto_examples/neighbors/
plot_classification.html#sphx-glr-auto-examples-neighbors-plot-classification-py. - [15]July大神. 支持向量机通俗导论(理解SVM的三层境界)[EB/OL]. http://blog.csdn.net/v_JULY_v/article/details/7624837.
- 点赞
- 收藏
- 关注作者


评论(0)