第十届蓝桥杯决赛JavaC组真题——详细答案对照(完整版)
【摘要】 目录A、奇数倍数B、递增序列C、平方拆分D、切割(挺过分的题)E、序列求和F、最长子序列G、数正方形H、矩阵计数I、大胖子走迷宫J、估计人数A、奇数倍数本题总分：5 分问题描述请你找到最小的整数 X 同时满足：X 是 2019 的整倍数X 的每一位数字都是奇数package action;public class demo { public static void main(String[...
目录
A、奇数倍数
本题总分：5 分
问题描述
请你找到最小的整数 X 同时满足：
X 是 2019 的整倍数
X 的每一位数字都是奇数
package action;
public class demo {
public static void main(String[] args) {
a: for (int i = 2019, n = 2019; true; n = i += 2019) {
do {
if ((n & 1) == 0)
continue a;
} while ((n /= 10) > 0);
System.out.println(i);
break;
}
}
}
B、递增序列
本题总分：5 分
问题描述
对于一个字母矩阵，我们称矩阵中的一个递增序列是指在矩阵中找到两个字母，它们在同一行，同一列，或者在同一 45 度的斜线上，这两个字母从左向右看、或者从上向下看是递增的。
例如，如下矩阵中
LANN
QIAO
有LN、LN、AN、AN、IO、AO、LQ、AI、NO、NO、AQ、IN、AN 等 13 个递增序列。注意当两个字母是从左下到右上排列时，从左向右看和从上向下看是不同的顺序。
对于下面的 30 行 50 列的矩阵，请问总共有多少个递增序列？（如果你把以下文字复制到文本文件中，请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt，内容与下面的文本相同）
VLPWJVVNNZSWFGHSFRBCOIJTPYNEURPIGKQGPSXUGNELGRVZAG
SDLLOVGRTWEYZKKXNKIRWGZWXWRHKXFASATDWZAPZRNHTNNGQF
ZGUGXVQDQAEAHOQEADMWWXFBXECKAVIGPTKTTQFWSWPKRPSMGA
BDGMGYHAOPPRRHKYZCMFZEDELCALTBSWNTAODXYVHQNDASUFRL
YVYWQZUTEPFSFXLTZBMBQETXGXFUEBHGMJKBPNIHMYOELYZIKH
ZYZHSLTCGNANNXTUJGBYKUOJMGOGRDPKEUGVHNZJZHDUNRERBU
XFPTZKTPVQPJEMBHNTUBSMIYEGXNWQSBZMHMDRZZMJPZQTCWLR
ZNXOKBITTPSHEXWHZXFLWEMPZTBVNKNYSHCIQRIKQHFRAYWOPG
MHJKFYYBQSDPOVJICWWGGCOZSBGLSOXOFDAADZYEOBKDDTMQPA
VIDPIGELBYMEVQLASLQRUKMXSEWGHRSFVXOMHSJWWXHIBCGVIF
GWRFRFLHAMYWYZOIQODBIHHRIIMWJWJGYPFAHZZWJKRGOISUJC
EKQKKPNEYCBWOQHTYFHHQZRLFNDOVXTWASSQWXKBIVTKTUIASK
PEKNJFIVBKOZUEPPHIWLUBFUDWPIDRJKAZVJKPBRHCRMGNMFWW
CGZAXHXPDELTACGUWBXWNNZNDQYYCIQRJCULIEBQBLLMJEUSZP
RWHHQMBIJWTQPUFNAESPZHAQARNIDUCRYQAZMNVRVZUJOZUDGS
PFGAYBDEECHUXFUZIKAXYDFWJNSAOPJYWUIEJSCORRBVQHCHMR
JNVIPVEMQSHCCAXMWEFSYIGFPIXNIDXOTXTNBCHSHUZGKXFECL
YZBAIIOTWLREPZISBGJLQDALKZUKEQMKLDIPXJEPENEIPWFDLP
HBQKWJFLSEXVILKYPNSWUZLDCRTAYUUPEITQJEITZRQMMAQNLN
DQDJGOWMBFKAIGWEAJOISPFPLULIWVVALLIIHBGEZLGRHRCKGF
LXYPCVPNUKSWCCGXEYTEBAWRLWDWNHHNNNWQNIIBUCGUJYMRYW
CZDKISKUSBPFHVGSAVJBDMNPSDKFRXVVPLVAQUGVUJEXSZFGFQ
IYIJGISUANRAXTGQLAVFMQTICKQAHLEBGHAVOVVPEXIMLFWIYI
ZIIFSOPCMAWCBPKWZBUQPQLGSNIBFADUUJJHPAIUVVNWNWKDZB
HGTEEIISFGIUEUOWXVTPJDVACYQYFQUCXOXOSSMXLZDQESHXKP
FEBZHJAGIFGXSMRDKGONGELOALLSYDVILRWAPXXBPOOSWZNEAS
VJGMAOFLGYIFLJTEKDNIWHJAABCASFMAKIENSYIZZSLRSUIPCJ
BMQGMPDRCPGWKTPLOTAINXZAAJWCPUJHPOUYWNWHZAKCDMZDSR
RRARTVHZYYCEDXJQNQAINQVDJCZCZLCQWQQIKUYMYMOVMNCBVY
ABTCRRUXVGYLZILFLOFYVWFFBZNFWDZOADRDCLIRFKBFBHMAXXpackage action;
import java.io.BufferedReader;
public class demo {
static String str = "VLPWJVVNNZSWFGHSFRBCOIJTPYNEURPIGKQGPSXUGNELGRVZAG"
+ "SDLLOVGRTWEYZKKXNKIRWGZWXWRHKXFASATDWZAPZRNHTNNGQF"
+ "ZGUGXVQDQAEAHOQEADMWWXFBXECKAVIGPTKTTQFWSWPKRPSMGA"
+ "BDGMGYHAOPPRRHKYZCMFZEDELCALTBSWNTAODXYVHQNDASUFRL"
+ "YVYWQZUTEPFSFXLTZBMBQETXGXFUEBHGMJKBPNIHMYOELYZIKH"
+ "ZYZHSLTCGNANNXTUJGBYKUOJMGOGRDPKEUGVHNZJZHDUNRERBU"
+ "XFPTZKTPVQPJEMBHNTUBSMIYEGXNWQSBZMHMDRZZMJPZQTCWLR"
+ "ZNXOKBITTPSHEXWHZXFLWEMPZTBVNKNYSHCIQRIKQHFRAYWOPG"
+ "MHJKFYYBQSDPOVJICWWGGCOZSBGLSOXOFDAADZYEOBKDDTMQPA"
+ "VIDPIGELBYMEVQLASLQRUKMXSEWGHRSFVXOMHSJWWXHIBCGVIF"
+ "GWRFRFLHAMYWYZOIQODBIHHRIIMWJWJGYPFAHZZWJKRGOISUJC"
+ "EKQKKPNEYCBWOQHTYFHHQZRLFNDOVXTWASSQWXKBIVTKTUIASK"
+ "PEKNJFIVBKOZUEPPHIWLUBFUDWPIDRJKAZVJKPBRHCRMGNMFWW"
+ "CGZAXHXPDELTACGUWBXWNNZNDQYYCIQRJCULIEBQBLLMJEUSZP"
+ "RWHHQMBIJWTQPUFNAESPZHAQARNIDUCRYQAZMNVRVZUJOZUDGS"
+ "PFGAYBDEECHUXFUZIKAXYDFWJNSAOPJYWUIEJSCORRBVQHCHMR"
+ "JNVIPVEMQSHCCAXMWEFSYIGFPIXNIDXOTXTNBCHSHUZGKXFECL"
+ "YZBAIIOTWLREPZISBGJLQDALKZUKEQMKLDIPXJEPENEIPWFDLP"
+ "HBQKWJFLSEXVILKYPNSWUZLDCRTAYUUPEITQJEITZRQMMAQNLN"
+ "DQDJGOWMBFKAIGWEAJOISPFPLULIWVVALLIIHBGEZLGRHRCKGF"
+ "LXYPCVPNUKSWCCGXEYTEBAWRLWDWNHHNNNWQNIIBUCGUJYMRYW"
+ "CZDKISKUSBPFHVGSAVJBDMNPSDKFRXVVPLVAQUGVUJEXSZFGFQ"
+ "IYIJGISUANRAXTGQLAVFMQTICKQAHLEBGHAVOVVPEXIMLFWIYI"
+ "ZIIFSOPCMAWCBPKWZBUQPQLGSNIBFADUUJJHPAIUVVNWNWKDZB"
+ "HGTEEIISFGIUEUOWXVTPJDVACYQYFQUCXOXOSSMXLZDQESHXKP"
+ "FEBZHJAGIFGXSMRDKGONGELOALLSYDVILRWAPXXBPOOSWZNEAS"
+ "VJGMAOFLGYIFLJTEKDNIWHJAABCASFMAKIENSYIZZSLRSUIPCJ"
+ "BMQGMPDRCPGWKTPLOTAINXZAAJWCPUJHPOUYWNWHZAKCDMZDSR"
+ "RRARTVHZYYCEDXJQNQAINQVDJCZCZLCQWQQIKUYMYMOVMNCBVY"
+ "ABTCRRUXVGYLZILFLOFYVWFFBZNFWDZOADRDCLIRFKBFBHMAXX";
static char[][] c = new char[30][50];
static int count = 0;
public static void main(String[] args) {
for (int i = 0; i < c.length; i++) {
for (int j = 0; j < c[i].length; j++) {
c[i][j] = str.charAt(i * c[i].length + j);
}
}
for (int i = 0; i < c.length; i++) {
for (int j = 0; j < c[i].length; j++) {
check(i, j);
}
}
System.out.println(count);
}
public static void check(int i, int j) {
// 右
for (int k = 1; k < c[i].length - j; k++) {
if (j + k < c[i].length && c[i][j] < c[i][j + k]) {
count++;
}
}
// 下
for (int k = 1; k < c.length - i; k++) {
if (i + k < c.length && c[i][j] < c[i + k][j]) {
count++;
}
}
// 右下角
for (int k = 1; k < c.length - i; k++) {
if (i + k < c.length && j + k < c[i].length && c[i][j] < c[i + k][j + k]) {
count++;
}
}
// 右上角
for (int k = 1; k < c.length; k++) {
if (i - k >= 0 && j + k < c[i].length && c[i][j] < c[i - k][j + k]) {
count++;
}
}
// 左下角
for (int k = 1; k < c.length; k++) {
if (i + k < c.length && j - k >= 0 && c[i][j] < c[i + k][j - k]) {
count++;
}
}
}
}这种题没啥犹豫的，暴力吧。
C、平方拆分
本题总分：10 分
问题描述
将 2019 拆分为若干个两两不同的完全平方数之和，一共有多少种不同的方法？
注意交换顺序视为同一种方法，例如 13^2 + 25^2 + 35^2 = 2019 与 13^2 + 35^2 +25^2 = 2019 视为同一种方法(^代表平方)。
package action;
public class demo {
static int count = 0;
public static void main(String[] args) {
dfs(2019, -1);
System.out.println(count);
}
public static void dfs(int num, int start) {
if (num < 0) {
return;
}
if (num == 0) {
count++;
} else {
for (int i = start + 1, high = (int) Math.sqrt(num); i <= high; i++)
dfs(num - i * i, i);
}
}
}D、切割(挺过分的题)
本题总分：10 分
问题描述
在 4 × 4 的方格矩阵中画一条直线。则直线穿过的方格集合有多少种不同的可能？这个里直线穿过一个方格当且仅当直线将该方格分割成面积都大于 0 的两部分。
答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。
package action;
import java.util.HashSet;
import java.util.Set;
public class demo {
final static int range = 100;
static Set<Integer> st = new HashSet<Integer>();
public static void main(String[] args) {
// 枚举直线标准方程 ax + by + c = 0的三个参数
for (int a = -range; a <= range; a++) {
for (int b = -range; b <= range; b++) {
for (int c = -range; c <= range; c++) {
int status = 0;
// 遍历16个格子
for (int x = 1; x <= 4; x++) {
for (int y = 1; y <= 4; y++) {
int pos = 0, neg = 0;// 记录正负个数
if (a * x + b * y + c > 0)
pos++;
if (a * x + b * y + c < 0)
neg++;
if (a * (x - 1) + b * (y - 1) + c > 0)
pos++;
if (a * (x - 1) + b * (y - 1) + c < 0)
neg++;
if (a * x + b * (y - 1) + c > 0)
pos++;
if (a * x + b * (y - 1) + c < 0)
neg++;
if (a * (x - 1) + b * y + c > 0)
pos++;
if (a * (x - 1) + b * y + c < 0)
neg++;
// 将上色的点集压缩成二进制的整数
status <<= 1;
if (pos * neg > 0)
status += 1;// 有正有负说明当前格子被直线穿过
}
}
st.add(status);// 记录当前点集
}
}
}
System.out.println(st.size());
}
}E、序列求和
本题总分：15 分
问题描述
学习了约数后，小明对于约数很好奇，他发现，给定一个正整数 t，总是可以找到含有 t 个约数的整数。小明对于含有 t 个约数的最小数非常感兴趣，并把它定义为 St 。
例如 S1 = 1, S2 = 2, S3 = 4, S4 = 6，· · · 。
现在小明想知道，前 60 个 Si 的和是多少？即 S1 + S2 + · · · + S60 是多少？
答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。
package action;
import java.util.Collections;
import java.util.List;
import java.util.Vector;
import static java.lang.Math.min;
import static java.lang.Math.pow;
public class demo {
static List<Integer> prim = new Vector<>();
public static void main(String[] args) {
initPrime();
long sum = 0;
for (int i = 1; i <= 60; i++) {
sum += dfs(resolve(i));
}
System.out.println(sum);
}
private static long dfs(List<Integer> vv) {
long ans = cal(vv);
if (vv.size() == 1)
return cal(vv);
for (int i = 0; i < vv.size() - 1; i++) {
for (int j = i + 1; j < vv.size(); j++) {
List<Integer> vvv = new Vector<>(vv.size() - 1);
for (int k = 0; k < vv.size(); k++) {
if (k != i && k != j)
vvv.add(vv.get(k));
}
Integer value_i = vv.get(i);
Integer value_j = vv.get(j);
vvv.add(value_i * value_j);
ans = min(ans, dfs(vvv));
}
}
return ans;
}
private static long cal(List<Integer> vv) {
Collections.sort(vv);
long ans = 1;
int j = 0;
for (int i = vv.size() - 1; i >= 0; i--) {
ans *= pow(prim.get(j++), vv.get(i) - 1);
}
return ans;
}
private static List<Integer> resolve(int now) {
List<Integer> vv = new Vector<>();
// 因子分解，存储在vv中
for (int j = 2; j * j <= now; j++) {
while (now % j == 0) {
vv.add(j);
now /= j;
}
}
if (now > 1)
vv.add(now);
if (vv.size() == 1)
vv.add(1);
return vv;
}
private static void initPrime() {
for (int i = 2; i <= 1e5; i++) {
boolean ok = true;
for (int j = 2; j * j <= i; j++) {
if (i % j == 0) {
ok = false;
break;
}
}
if (ok)
prim.add(i);
}
}
}
看到有人说结果是：【101449】，但是我能确定【292809912969717649】绝对是给分了的。
F、最长子序列
时间限制: 1.0s 内存限制: 512.0MB 本题总分：15 分
问题描述
我们称一个字符串 S 包含字符串 T 是指 T 是 S 的一个子序列，即可以从字符串 S 中抽出若干个字符，它们按原来的顺序组合成一个新的字符串与 T 完全一样。
给定两个字符串 S 和 T，请问 T 中从第一个字符开始最长连续多少个字符被 S 包含？
输入格式
输入两行，每行一个字符串。第一行的字符串为 S，第二行的字符串为 T。
两个字符串均非空而且只包含大写英文字母。
输出格式
输出一个整数，表示答案。
测试样例1
Input：
ABCDEABCD
AABZ
Output：
3
评测用例规模与约定
对于 20% 的评测用例，1 ≤ |T| ≤ |S | ≤ 20；
对于 40% 的评测用例，1 ≤ |T| ≤ |S | ≤ 100；
对于所有评测用例，1 ≤ |T| ≤ |S | ≤ 1000。
package action;
import java.util.Scanner;
public class demo {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s1 = sc.next();
String s2 = sc.next();
sc.close();
int n1 = 0;
int n2 = 0;
int sum = 0;
for (; n1 < s1.length(); n1++) {
if (s1.charAt(n1) == s2.charAt(n2)) {
sum++;
n2++;
}
}
System.out.println(sum);
}
}
G、数正方形
时间限制: 1.0s 内存限制: 512.0MB 本题总分：20 分
问题描述
在一个 N × N 的点阵上，取其中 4 个点恰好组成一个正方形的 4 个顶点，一共有多少种不同的取法？
由于结果可能非常大，你只需要输出模 109 + 7 的余数。
（如：图7）所示的正方形都是合法的。
输入格式
输入包含一个整数 N。
输出格式
输出一个整数代表答案。
测试样例1
Input：
4
Output：
20
评测用例规模与约定
对于所有评测用例，2 ≤ N ≤ 1000000。
package action;
import java.math.BigInteger;
import java.util.Scanner;
public class demo {
final static BigInteger mod = BigInteger.valueOf(1000_000_007);
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
sc.close();
BigInteger ans = BigInteger.ZERO;
for (int i = 1; i <= n; i++) {
BigInteger x = BigInteger.valueOf(n - i);
ans = ans.add(BigInteger.valueOf(i).multiply(x.pow(2))).mod(mod);
}
System.out.println(ans.longValue());
}
}
H、矩阵计数
时间限制: 1.0s 内存限制: 512.0MB 本题总分：20 分
问题描述
一个 N × M 的方格矩阵，每一个方格中包含一个字符 O 或者字符 X。
要求矩阵中不存在连续一行 3 个 X 或者连续一列 3 个 X。
问这样的矩阵一共有多少种？
输入格式
输入一行包含两个整数 N 和 M。
输出格式
输出一个整数代表答案。
测试样例1
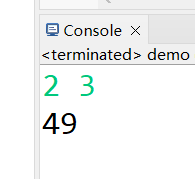
Input：
2 3
Output：
49
评测用例规模与约定
对于所有评测用例，1 ≤ N, M ≤ 5。
package action;
import java.util.Scanner;
public class demo {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n1 = sc.nextInt();
int n2 = sc.nextInt();
sc.close();
int a[][] = new int[n1][n2];
int sum = 0;
for (int t = 0; t < Math.pow(2, n1 * n2); t++) {
int x = 0;
// 将数组赋值
for (int i = 0; i < n1; i++) {
for (int j = 0; j < n2; j++) {
if ((t >> x & 1) == 1) {
a[i][j] = 1;
}
x++;
}
}
if (check(a)) {// 检查数组
} else {
sum++;
}
// 数组清空
for (int i = 0; i < n1; i++) {
for (int j = 0; j < n2; j++) {
a[i][j] = 0;
}
}
}
System.out.println(sum);
}
private static boolean check(int[][] a) {
int x = 0;
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < a[0].length; j++) {
if (a.length - i > 2 & a[i][j] == 1) {
if (a[i + 1][j] == 1 & a[i + 2][j] == 1) {
x = 1;
return true;
}
}
if (a[0].length - j > 2 & a[i][j] == 1) {
if (a[i][j + 1] == 1 & a[i][j + 2] == 1) {
x = 1;
return true;
}
}
}
}
if (x == 1) {
return true;
}
return false;
}
}
I、大胖子走迷宫
时间限制: 1.0s 内存限制: 512.0MB 本题总分：25 分
问题描述
小明是个大胖子，或者说是个大大胖子，如果说正常人占用 1 × 1 的面积，小明要占用 5 × 5 的面积。由于小明太胖了，所以他行动起来很不方便。当玩一些游戏时，小明相比小伙伴就吃亏很多。
小明的朋友们制定了一个计划，帮助小明减肥。计划的主要内容是带小明玩一些游戏，让小明在游戏中运动消耗脂肪。走迷宫是计划中的重要环节。
朋友们设计了一个迷宫，迷宫可以看成是一个由 n × n 个方阵组成的方阵，正常人每次占用方阵中 1 × 1 的区域，而小明要占用 5 × 5 的区域。小明的位置定义为小明最正中的一个方格。迷宫四周都有障碍物。
为了方便小明，朋友们把迷宫的起点设置在了第 3 行第 3 列，终点设置在了第 n-2 行第 n-2 列。
小明在时刻 0 出发，每单位时间可以向当前位置的上、下、左、右移动单位 1 的距离，也可以停留在原地不动。小明走迷宫走得很辛苦，如果他在迷宫里面待的时间很长，则由于消耗了很多脂肪，他会在时刻 k 变成一个胖子，只占用 3 × 3 的区域。如果待的时间更长，他会在时刻 2k 变成一个正常人，只占用 1 × 1 的区域。注意，当小明变瘦时迷宫的起点和终点不变。
请问，小明最少多长时间能走到迷宫的终点。注意，小明走到终点时可能变瘦了也可能没有变瘦。
输入格式
输入的第一行包含两个整数 n, k。
接下来 n 行，每行一个由 n 个字符组成的字符串，字符为 + 表示为空地，
字符为 * 表示为阻碍物。
输出格式
输出一个整数，表示答案。
测试样例1
Input：
9 5
+++++++++
+++++++++
+++++++++
+++++++++
+++++++++
***+*****
+++++++++
+++++++++
+++++++++
Output：
16
评测用例规模与约定
对于 30% 的评测用例，1 ≤ n ≤ 50。
对于 60% 的评测用例，1 ≤ n ≤ 100。
对于所有评测用例，1 ≤ n ≤ 300，1 ≤ k ≤ 1000。
package action;
import java.io.IOException;
import java.io.InputStream;
import java.util.LinkedList;
import java.util.Queue;
public class demo {
public static void main(String[] args) {
InputReader in = new InputReader(System.in);
int n = in.nextInt(), k = in.nextInt();
if (n <= 5)
System.out.print('0');
else {
int map[][] = new int[n][n], INF = 0x3F3F3F3F;
boolean[][] visit = new boolean[n][n];
for (int i = 0, hi = n - 1; i <= hi; i++) {
if (i < hi)
map[1][i] = map[hi - 1][i] = map[i][1] = map[i][hi - 1] = 1;
map[0][i] = map[hi][i] = map[i][0] = map[i][hi] = 2;
}
int[] os2i = { -1, -1, 0, 1, 1, 1, 0, -1 };
int[] os2j = { 0, 1, 1, 1, 0, -1, -1, -1 };
int[] os1i = { -2, -2, -2, -1, 0, 1, 2, 2, 2, 2, 2, 1, 0, -1, -2, -2 };
int[] os1j = { 0, 1, 2, 2, 2, 2, 2, 1, 0, -1, -2, -2, -2, -2, -2, -1 };
for (int i = 0, x, y; i < n; i++)
for (int j = 0; j < n; j++) {
if (in.split() == '*') {
map[i][j] = INF;
for (int l = 0; l < 8; l++) {
x = i + os2i[l];
y = j + os2j[l];
if (x < 0 || x >= n || y < 0 || y >= n || map[x][y] > 2)
continue;
map[x][y] = 2;
}
for (int l = 0; l < 16; l++) {
x = i + os1i[l];
y = j + os1j[l];
if (x < 0 || x >= n || y < 0 || y >= n || map[x][y] > 1)
continue;
map[x][y] = 1;
}
}
}
class Step {
int x, y, time;
Step(int x, int y, int time) {
this.x = x;
this.y = y;
this.time = time;
}
Step relax() {
this.time++;
return this;
}
}
Queue<Step> queue = new LinkedList();
int[] offsetX = { -1, 0, 1, 0 };
int[] offsetY = { 0, 1, 0, -1 };
int endX = n - 3, endY = n - 3;
queue.offer(new Step(2, 2, 0));
while (queue.size() > 0) {
Step now = queue.poll();
if (now.x == endX && now.y == endY) {
System.out.print(now.time);
break;
}
for (int i = 0, x, y, s; i < 4; i++) {
x = now.x + offsetX[i];
y = now.y + offsetY[i];
s = now.time / k;
if (x < 0 || x >= n || y < 0 || y >= n || visit[x][y] || map[x][y] > s)
continue;
visit[x][y] = true;
queue.offer(new Step(x, y, now.time + 1));
}
queue.offer(now.relax());
}
}
}
static class InputReader {
InputStream in;
int next, len;
byte[] buff;
InputReader(InputStream in) {
this(in, 8192);
}
InputReader(InputStream in, int buffSize) {
this.buff = new byte[buffSize];
this.next = this.len = 0;
this.in = in;
}
int getByte() {
if (next >= len)
try {
next = 0;
len = in.read(buff);
if (len == -1)
return -1;
} catch (IOException e) {
e.fillInStackTrace();
}
return buff[next++];
}
int split() {
int c = getByte();
while (c <= 32 || c == 127)
c = getByte();
return c;
}
int nextInt() {
int n = 0, c = split();
boolean flag = true;
if (c == '-') {
c = getByte();
flag = false;
}
while (c >= '0' && c <= '9') {
n = n * 10 + (c & 0xf);
c = getByte();
}
return flag ? n : -n;
}
}
}
J、估计人数
时间限制: 1.0s 内存限制: 512.0MB 本题总分：25 分
问题描述
给定一个 N × M 的方格矩阵，矩阵中每个方格标记 0 或者 1 代表这个方格是不是有人踩过。
已知一个人可能从任意方格开始，之后每一步只能向右或者向下走一格。
走了若干步之后，这个人可以离开矩阵。这个人经过的方格都会被标记为 1，包括开始和结束的方格。注意开始和结束的方格不需要一定在矩阵边缘。
请你计算至少有多少人在矩阵上走过。
输入格式
输入第一行包含两个整数 N、M。
以下 N 行每行包含 M 个整数 (0/1)，代表方格矩阵。
输出格式
输出一个整数代表答案。
测试样例1
Input：
5 5
00100
11111
00100
11111
00100
Output：
3
评测用例规模与约定
对于所有评测用例，1 ≤ N, M ≤ 20，标记为 1 的方格不超过 200 个。
package action;
import java.io.IOException;
import java.io.InputStream;
import java.util.Arrays;
public class demo {
static int V = 1;
static int source[];
static boolean graph[][], marked[];
public static void main(String[] args) {
InputReader in = new InputReader(System.in);
int n = in.nextInt(), m = in.nextInt();
int idx[][] = new int[n + 1][m + 1];
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (in.split() == '1')
idx[i][j] = V++;
graph = new boolean[V][V];
marked = new boolean[V];
source = new int[V];
for (int i = 0, v; i < n; i++)
for (int j = 0; j < m; j++)
if (idx[i][j] > 0) {
v = idx[i][j];
if (idx[i + 1][j] > 0)
graph[v][idx[i + 1][j]] = true;
if (idx[i][j + 1] > 0)
graph[v][idx[i][j + 1]] = true;
}
for (int k = 1; k < V; k++)
for (int i = 1; i < V; i++)
for (int j = 1; j < V; j++)
graph[i][j] |= graph[i][k] & graph[k][j];
int cnt = 0;
for (int i = 1; i < V; i++) {
Arrays.fill(marked, false);
cnt += dfs(i) ? 1 : 0;
}
System.out.print(V - cnt - 1);
}
static boolean dfs(int v) {
for (int i = 1; i < V; i++) {
if (graph[v][i]) {
if (marked[i])
continue;
marked[i] = true;
if (source[i] == 0 || dfs(source[i])) {
source[i] = v;
return true;
}
}
}
return false;
}
static class InputReader {
InputStream in;
int next, len;
byte[] buff;
InputReader(InputStream in) {
this(in, 8192);
}
InputReader(InputStream in, int buffSize) {
this.buff = new byte[buffSize];
this.next = this.len = 0;
this.in = in;
}
int getByte() {
if (next >= len)
try {
next = 0;
len = in.read(buff);
if (len == -1)
return -1;
} catch (IOException e) {
e.fillInStackTrace();
}
return buff[next++];
}
int split() {
int c = getByte();
while (c <= 32 || c == 127)
c = getByte();
return c;
}
int nextInt() {
int n = 0, c = split();
boolean flag = true;
if (c == '-') {
c = getByte();
flag = false;
}
while (c >= '0' && c <= '9') {
n = n * 10 + (c & 0xf);
c = getByte();
}
return flag ? n : -n;
}
}
}
这套题有几个题应该是给本科的，专门刁难了一下大专的孩子们，不道义啊。
【版权声明】本文为华为云社区用户原创内容，转载时必须标注文章的来源（华为云社区）、文章链接、文章作者等基本信息， 否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）