宽带接收机中的非均匀采样技术研究之总论（2018/8/18）（第一篇）
宽带接收机中的非均匀采样技术研究为论文地址，这里再次边阅读边解读这篇文章。
直系师兄的论文，以及实验室的一个小项目，比较有发言权。
论文概述
以下是摘要部分，觉得很重要，它给出了整体研究的内容的总结，这给我们看论文提供了方向。
让我们知道我们从论文需要知道什么重点？
例如：
如何设计非均匀采样平台？
非均匀时钟是如何产生的？
GTH是如何工作的？
采样保持器如何工作？
ADC采样时钟和非均匀时钟之间的关系？
ADC和采样保持器怎么样协调工作才能满足要求？
OMP算法如何应用到本采样后的数据的恢复上？
等等都是我们想要了解的东西，都是看这篇论文的欲望！
想到什么就写了什么？所以问题之间的逻辑可能不是太严谨。
本文在压缩感知理论和非均匀采样理论的基础之上，研究非均匀采样平台的硬件实现，完成对频域稀疏信号的直接压缩采样，并利用压缩感知重构算法中的OMP算法对采样数据进行信号重构。
主要研究内容具体如下：
1. 在分析压缩感知理论的数学模型，包括信号稀疏表示，观测矩阵设计以及信号重构等的基础上，结合非均匀采样的相关理论构建非均匀采样硬件模型。
2. 以非均匀采样器(NUS)模型为核心设计非均匀采样平台，利用采样率为400MHz的ADC芯片实现对2GHz范围内的频域稀疏信号进行压缩采样，从而实现对奈奎斯特采样率的10倍压缩。
首先利用非均匀时钟控制采样保持器对信号进行非均匀采样，并让采样保持器在ADC芯片的采样时刻输出幅度为当前采样值的信号，然后通过ADC芯片对采样保持器的输出信号进行采样从而实现对信号的非均匀采样。
3. 非均匀时钟的设计是本文的关键。为了保证采样保持器具有上述输出特性，非均匀时钟和ADC采样时钟必须具有特定的时序关系。由于ADC采样时钟可视为是固定不变的，所以在设计非均匀时钟时，以ADC采样时钟作为参考基准。
同时为了便于使用OMP算法完成信号重构，在设计非均匀时钟时需要保证非均匀采样的采样间隔都是潜在奈奎斯特采样间隔的整数倍。根据FPGA的GTH输出特性，我们采用GTH输出高速伪随机比特流的方式来产生非均匀时钟，从而将非均匀时钟的设计转换为对伪随机序列的设计。通过设计伪随机序列，使得非均匀采样时刻都随机落在ADC相邻两次采样时刻之间。
4. 根据硬件设计方案，完成硬件平台的搭建。并在现有实验室条件下对非均匀采样平台进行测试，并给出具体结果。
本研究针对的对象，以及原因及可行性。
由于电磁信号在频域具有明显的稀疏性，所以可以结合非均匀采样技术和压缩感知技术，设计合适的非均匀采样模型，在采样速率远低于奈奎斯特采样速率的情况下对宽频带信号进行采样，并根据采样数据利用压缩感知重构算法对原始信号进行重构及信息提取，从而降低实际宽带接收机中 ADC 的采样率，这对提高电子侦察中的宽带接收机在处理宽频带信号方面的能力具有重要的意义。
非均匀采样技术的优势
特定条件下，和均匀采样相比非均匀采样具有明显优势。例如对稀疏信号进行采样时，均匀采样数据会包含大量的冗余数据，而利用稀疏采样和压缩感知技术可以减少数据冗余的同时提升采样性能 。
目前国内外在非均匀采样技术方面的研究
（非均匀采样研究的现状）
目前国内外在非均匀采样技术方面的研究主要包括以下几个方面：
(1) 对原始信号的重构和分析 。对原始信号的重构一直是非均匀采样理论中最基本的问题。非均匀采样早期的研究也多集中在此。当前均匀采样理论已经发展的比较成熟，所以在非均匀采样的信号重构方面的研究主要是利用内插公式和均匀重采样技术，将非均匀采样转化为均匀采样，然后利用成熟的均匀采样理论进行分析处理。
(2) 域变换方法及其快速算法的研究 。通过将信号由时域转换到频域可以获得许多时域中不易得到的信息。将非均匀采样信号向其他域转换的方法自然成为一个研究重点。这些变换方法包括非均匀采样信号的傅里叶变换和改进后的快速傅里叶变换。
(3) 采样模型的研究 。这类研究主要是对非均匀采样方式的设计。针对不同的信号，设计特殊的采样方式有效减小噪声和谐波的影响，提高采样的性能。随着理论研究和实际工程的不断深入，非均匀采样理论已经成为现代数字信号处理的重要组成部分。
本文的主要内容和结构
本文通过分析压缩感知理论的数学模型，包括信号稀疏表示，观测矩阵设计以及信号重构等，结合非均匀采样的相关理论构建非均匀采样硬件模型。并最终以非均匀采样器(NUS)模型为基本框架，研究非均匀采样平台的硬件实现，在较宽的频率范围内对频域稀疏信号进行直接压缩采样，在论文的最后给出了硬件平台的真实测试结果。
第一章 绪论。本章主要介绍论文研究的背景及意义，分析当前雷达和电子战系统在对宽频信号进行处理时所面临的困难。然后介绍当前国内外在非均匀采样和压缩感知领域的研究现状，最后介绍本文的研究内容及结构安排。
第二章 压缩感知理论及非均匀采样硬件模型。本章主要介绍压缩感知理论的数学模型，包括信号稀疏表示，观测矩阵设计以及信号重构等，并结合非均匀采样的相关理论介绍本文选用的非均匀采样器采样模型及 OMP 信号重构算法。
第三章 非均匀采样平台的硬件设计。本章针对第二章介绍的非均匀采样器采样模型，设计非均匀采样平台的硬件实现方案。首先对该平台的整体设计结构进行介绍，然后对非均匀时钟的时序特征及产生方法进行了详尽的论述。针对平台设计要求介绍了在器件选择方面的考虑并对所使用芯片进行介绍。
第四章 非均匀采样平台的硬件实现。本章主要是对非均匀采样平台具体的硬件实现进行论述。对所设计的非均匀采样平台按功能进行模块划分，并对各个模块的功能及技术要点进行介绍。
第五章 实验测试及结果分析。本章主要完成对非均匀采样平台的测试。首先介绍了非均匀采样平台完成后所需要进行的调试工作及调试方法。然后通过一系列测试实验对平台的性能进行测试并给出具体结果。
下面对此分析总结：
第一章的绪论在上面已经介绍过了。
下面直接看第二章： 压缩感知理论
说到压缩感知，就不得不与传统的压缩过程进行比较：
下图为传统的压缩过程：
如图 2.1 所示，对于可压缩的信号，首先需要根据奈奎斯特定理对原始信号进行高速采样，然后再完成采样数据的压缩。在压缩数据的过程中，需要根据特殊的算法对大量的采样数据进行筛选，最后保留有用的数据。传统的压缩方法在资源上造成了很大的浪费，而且对信号进行筛选时的计算量也是极大的，这些都严重地影响了压缩的效率。
压缩感知(CS)理论的出现为信号采集领域提供了一种全新的思想。它打破了奈奎斯特采样理论对采样率的束缚，即使在采样速率远低于奈奎斯特速率的情况下，压缩感知理论指出，对满足一定要求的信号进行合适的压缩采样依然可以利用采样信号对原始信号以极大概率完成信号重构 。
与奈奎斯特采样理论不同，CS 理论对采样率的要求不再是根据信号带宽，而是由信号的稀疏性决定。CS 理论以矩阵变换为基本手段，首先选择合适的稀疏变换基，对信号进行稀疏表示，然后通过观测矩阵对稀疏化的信号进行观测，将原始信号从高维空间向较低维空间投影，最终通过求解凸优化问题以极高的概率实现对原始信号的重构 。
下面是压感的经典解释：
假设 X 是长度为 N 的一维离散信号。如果信号 X 在正交基 Ψ 内可以进行稀疏表示X = Ψa，则可以利用一个 M*N的观测矩阵 Φ ，其中 M<<N 。通过对信号 X 做矩阵变换，便可以得到观测数据 Y =ΦΨa = Aa ，其中 Y 是M*1维的向量， X = Ψa ，如果保证 Φ 和 Ψ 是两个不相关的矩阵。则可以通过观测数据 Y 重构出原始信号X ，图 2.2 是压缩感知的一般流程：
！！！！！！
注：压感针对的对象是X，也就是一个有限长（N）的一维离散信号X，然后对这个信号进行一个稀疏变换，这就需要找到一个稀疏矩阵
，使得
需要注意的是如果X本身就是一个稀疏信号的话，就不要稀疏变换了，当然也可以认为稀疏矩阵就是一个N维的单位阵。
之后设计一个观测矩阵
该低维的观测信号Y里面的信息都是精华，因为观测矩阵的作用就是去除稀疏信号里面的无用信号，留着一些有用的信号，该有用信号指的是对于恢复出原来信号X有用的信息。
那么如何由观测矩阵来恢复出稀疏信号
下面会说，但这里强调一下，如果恢复除了
恢复过程涉及到很多算法，当然可以使用其中一种来恢复出原始信号（OMP），但是如果会使用多种恢复算法，并且能比较其优劣，不失为一种个人造诣！
下面来说说恢复过程吧：
如图 2.2 所示，其中， a 表示投影系数。构造和 Ψ 不相关的观测矩阵 Φ ，其中 Φ 是 M*N 维的矩阵。由此， X 的观测值可以表示为： Y = ΦX = ΦΨa ，最后通过求解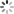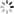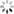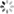 范数限制下的凸优化问题来得到 X 的估计值以及其在 Ψ 下的投影系数 a ：
上式中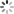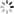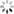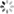 是 X 在基 Ψ 上的最稀疏解。
压缩感知理论可以分为以下三个部分内容：
(1) 对自然信号进行稀疏表示；
(2) 设计观测矩阵；
(3) 信号重构算法。
下面将分别对这三个方面进行介绍。
下一篇博文更新第一个问题：
对自然信号进行稀疏表示。
宽带接收机中的非均匀采样技术研究之自然信号的稀疏表示（2018/8/18）（第二篇）
文章来源: reborn.blog.csdn.net，作者：李锐博恩，版权归原作者所有，如需转载，请联系作者。
原文链接：reborn.blog.csdn.net/article/details/81807981
- 点赞
- 收藏
- 关注作者
评论（0）