一种以超体积测量（S度量）为选择准则的EMO算法-SMS-EMOA

SMS-EMOA: Multiobjective selection based on dominated hypervolume

原文：https://www.sciencedirect.com/science/article/pii/S0377221706005443

摘要：超体积测度是比较进化多目标优化算法(EMOA)结果的最常用方法之一。本文将设计一种稳定状态的EMOA，它将非占优排序的概念与基于超体积测度的选择算子结合起来。该算法计算具有界大小的一组分布比较好的解，从而聚焦于Pareto前沿的感兴趣的区域。

0.写作动机

在实践中，决策者只希望评价数量有限的帕累托最优解。这是由于在实践中实现的解决办法的适用时间有限。

1.介绍

首先是Pareto optimization，提供了一组目标函数f1，...，n，S→R定义为要在搜索空间S上的寻找最优值。在Pareto优化中，目标是检测Pareto-最优集，或者至少是这个集合的一个很好的近似。

接下来介绍一个衡量非支配集质量的测量是超体积测量或S度量。到目前为止，研究主要集中在利用S度量进行多目标优化的两种方法：Flischer建议将多目标优化问题转化为单目标优化问题，方法是使有限个非支配点集的S度量最大化。Knowles等人在EMOA存档策略中使用S度量。

我们的目标是构造一种算法，其中S度量控制EMOA的选择算子，以便找到一组在Pareto前沿分布良好的解。这个EMOA的基本思想是整合种群中的新点，如果替换一个成员会增加人口所涵盖的超体积量（变得更好）。因此，提出了一个稳态(μ+1)-EMOA【由于超体积的计算量很大，该文使用稳态选择方案，每一代创建一个点，删除一个。所以选择算子至少计算u+1个度量。】，即所谓的S度量选择EMOA(SMS-EMOA).

2.超体积测量

超体积度量或S度量最初是由Zitzler和Thiele[3]提出的，他们称其为所覆盖空间的大小或支配空间的大小。

在进化多目标优化（EMO）中，算法在性能空间中产生一组点作为Pareto前沿的估计。 需要定量测量来估计估计数据点与真正帕累托前沿的接近程度。

其中一个措施是超体积指标，它给出了估计的Pareto前沿（P）和参考点（R）之间的超体积。 但是，严格计算指标非常耗时。 该工具使用蒙特卡罗方法通过计算性能空间中由帕累托前沿支配的一组随机点的百分比来估计超体积。

CoelloCoello、VanVeldhuizen和Lamont将其描述为由非支配点mi和参考点xref定义的超立方体结合的Lebesgue量度Λ，如公式1。

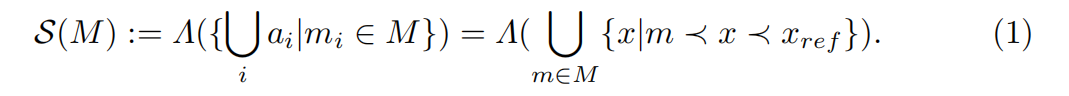
并且准确计算S度规需要一个归一化的正目标空间和仔细选择参考点。诺尔斯和科恩给出了一个例子，两个帕累托前沿，A和B，在二维情况下。它们显示S(A)<S(B)或S(B)<S(A)取决于参照点的选择。

同时，Flischer证明了S的最大值是有限真Pareto前沿的一个充要条件，如下图。

之后在另一篇文章中看到对于S度量的解释：给出了目标空间中的一个点Z1和一个以被它支配的参考向量Zref，并将受其控制和有界的区域定义为集合。定义如下图，其中<是支配的意思。

对于一个非支配向量集A，以及一个由A所有成员所支配的参考向量Zref，由A支配的区域和以Zref为界限被定义为以下集合：

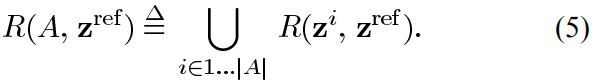
A相对于参考向量的度量是集合R（A，Zref）的“超体积”或Lebesgue积分。Zref一般取种群内最大（最小）值。

3.本文算法

SMS-EMOA的一个基本特性是，它在一个稳态方法（每代只产生一个后代，评估后立即加入下一代的演化）中更新一个群体，即在每次迭代中只生成一个新的个体。算法1描述了基本算法，从初始种群出发，利用随机变异算子生成一个新个体。与其他将非支配个体存储在档案中的策略不同，SMS-EMOA将非支配和支配的个人群体保持在不变的规模上。为了决定哪些人在选择中被淘汰，还必须在支配解决方案中建立参数选择。

算法2描述减少雇用的替换程序。为了确定哪些个体存在于种群中，采用了从著名的NSGA-II中筛选出的Pareto前沿排名的概念。

1.使用快速非支配排序算法计算关于非支配水平(或等级)的Pareto前沿，直到Ri不能在种群G中放下（即将父代（N个个体）和子代（N个个体）并在一起，再选出前N个比较好的个体）

2.之后，将一个个体从最差的排名中丢弃。如果前沿Ri包含了|Ri|>1(支配的个体大于一个)个体，那么对于s∈Ri（Ri层Pareto前沿中包括s））的这个个体就会被消除，从而使其最小化。

△S（s，Ri）表示s的超体积，超体积越小，则这个个体的作用越小，应该被除去。对于两个目标函数，我们取最坏的非支配前沿的点，并根据最初的目标函数f1的值对它们进行排序。我们得到另一个按f2值降序排序的序列。因为这些点是相互非支配的。△S（s，Ri）计算如下，对于Ri来说：Ri={s1，...，s|Ri|}

4.拥挤算子和超体积：

首先介绍一下拥挤距离：一个个体在目标空间所能生成的最大的矩形（该矩形不能触碰目标空间其他的点）的边长之和、

如图所示，对于X4，X5来说，用拥挤距离计算X5更好。而用S度量来说，X4更好，但在实际应用中，解决方案X4比解决方案X5更有趣，因为在X5附近，目标f2中的小收益只能以目标f1付出很大的代价来实现，即寻求一个平衡的解决方案。可以看出在SMS-EMOA算法中，位于Pareto前部凸面拐点附近的较好的折中解在SMS-EMOA中比在NSGA-Ⅱ算法中得到了更好的排序。

5.总结

本文设计的SMS-EMOA算法是一种很有前途的Pareto优化算法。特别是如果需要少量的、有限的解决方案，并强调平衡权衡的领域，但它的选择时间复杂度较高，一般在非支配级只剩一层时应用它，从而取得很好的结果。

最后，博主的学习笔记都是根据自己的理解意译的，可能与原文并不完全相符，而且博主作为初学者理解尚不深刻，所以可能存在一些不足之处，若有疑问可与博主进行讨论。博主翻译的文章是已公开发表的英文文献，仅供学习使用，如有侵权请联系博主删除。

文章来源: blog.csdn.net，作者：αβγθ，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/weixin_38022166/article/details/99648357