EM算法和GMM(中)
【摘要】 GMM,高斯混合模型,也可以简写为MOG。高斯模型就是用高斯概率密度函数(正态分布曲线)精确地量化事物,将一个事物分解为若干的基于高斯概率密度函数(正态分布曲线)形成的模型。
单高斯,混合高斯,多变量混合高斯
单高斯是一维变量一个模型,混合高斯是一维变量多个模型,多变量混合高斯是多个维度变量多个模型。
GMM的表达式为k个高斯分布的叠加
GMM,高斯混合模型,也可以简写为MOG。高斯模型就是用高斯概率密度函数(正态分布曲线)精确地量化事物,将一个事物分解为若干的基于高斯概率密度函数(正态分布曲线)形成的模型。
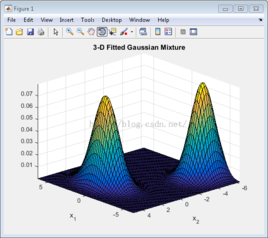
单高斯,混合高斯,多变量混合高斯
单高斯是一维变量一个模型,混合高斯是一维变量多个模型,多变量混合高斯是多个维度变量多个模型。
GMM的表达式为k个高斯分布的叠加


文章来源: maoli.blog.csdn.net,作者:刘润森!,版权归原作者所有,如需转载,请联系作者。
原文链接:maoli.blog.csdn.net/article/details/89216525
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)