@toc

1、算法概述

Dijkstra算法用来计算一个点到其他所有点的最短路径的算法，是一种单源最短路径算法。也就是说，只能计算起点只有一个的情况。

Dijkstra算法的时间复杂度是 $O(n^3)$，它不能处理存在负边权的情况。

算法描述：

设起点为s,dis[v]表示从s到v的最短路径长度

• 初始化： $dis[v]=\infty (v \neq s);dis[s]=0$

For(i=1;i<=n;i++){
	1.在没有被访问过的点钟找一个顶点u使得dis[u]是最小的。
	2.u标记为已确定最短路径。
	3.For与u相连的每个未确定最短路径的顶点v
	if(dis[u]+w[u][v]<dis[v]){
		dis[v]=dis[u]+w[u][v];
	}
}

• 算法结束：dis[v]为s到v的最短距离。

2、算法实例

对于下图，我们想求出从顶点1到其他所有顶点的最短距离。

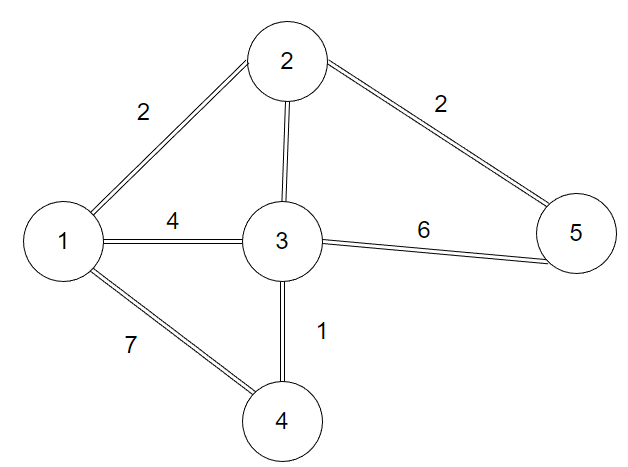
算法开始时，我们设置dis[1]=0(自己到自己最短距离肯定是0),其他的点 $dis[i]=\infty$。

这里规定两种类型的顶点，代码中可以设置一个boolean数组来表示

• 蓝点：未确定最短路径的点。
• 白点：已经确定最短路径的点

第一轮，dis[1]=0最小，将1变成白点。对所有的蓝点做出修改。此时由于刚开始其他点在dis数组中都是无穷大，所以只要1能到达的点，我们都会更新，更新之后的dis数组如下(不考虑下标为0):

$$[0,\infty,\infty,\infty,\infty ]->[0,2,4,7,\infty]$$

第二轮，dis[2]=2最小，将2变成白点。对蓝点做出修改。

由于 $dis[2]+a[2][3]=2+1=3<dis[3]=4$,则令 $dis[3]=3$

由于 $dis[2]+a[2][5]=2+2=4<dis[5]=\infty$,则令 $dis[5]=4$

$$[0,2,4,7,\infty]->[0,2,3,7,4]$$

第三轮，dis[3]=3最小，将3变成白点。对蓝点做出修改。

由于 $dis[3]+a[3][4]=3+1=4<dis[4]=7$，则令 $dis[4]=4$

由于 $dis[3]+a[3][5]=4+6=10>dis[5]=4$,所以不更新dis[5]

这里给出了此时为什么不更新dis[5]，其他步骤中有关不更新的就不再列出了。

$$[0,2,3,7,4]->[0,2,3,4,4]$$

第四轮，dis[4]=4最小，将4变成白点。对蓝点做出修改

此时并不符合更新条件。

第五轮，dis[5]=4最小，将5变成白点，此时所有的点都是白点了，搜索结束。

最终的dis数组为: $[0,2,3,4,4]$，数组的值分别表示顶点1到其他各个顶点的最短距离。

3、实战案例

3.1 题目描述

小明是蓝桥王国的王子，今天是他登基之日。

在即将成为国王之前，老国王给他出了道题，他想要考验小明是否有能力管理国家。

题目的内容如下：

蓝桥王国一共有N个建筑和M条单向道路，每条道路都连接着两个建筑，每个建筑都有自己编号，分别为 $1\sim N$。(其中皇宫的编号为1).

国王想让小明回答从皇宫到每个建筑的最短路径是多少，但紧张的小明此时已经无法思考，请你编写程序帮助小明回答国王的考核。

输入描述

输入第一行包含两个正整数N,M。

第2到M+1行每行包含三个正整数u,v,w，表示 $u\to v$之间存在一条距离为w的路。

$$1\le N\le 3\times10^5,1\le m\le10^6,1\le u_i,v_i\le N,0\le w_i \le 10^9$$

输出描述

输出仅一行，共N个数，粉笔表示从皇宫到编号为 $1\sim N$建筑的最短距离，两两之间用空格隔开。(如果无法到达则输出-1)

输入输出样例

输入

3 3
1 2 1
1 3 5
2 3 2

输出

0 1 3

3.2 解题思路与代码实现

很明显，这是一道求最短路径的题，而且还是单源最短路径，因为只问了从皇宫到其他节点之间的最短距离，那我们使用Dijkstra算法即可很快实现。

import java.util.Arrays;
import java.util.Scanner;

//最短路径，邻接矩阵实现
public class Dijkstra {
    public static int n,m,s;
    static int[][] mp;  //地图：邻接矩阵存储
    static int[] dis;   //dis[v]：从s到v的最短路径长度
    static boolean[] vis;//标记是否已经被访问
    static int[] pre;   //记录前驱，方便最后输出最短路径
    public static void initmp(){
        for (int[] ints : mp) {
            Arrays.fill(ints, Integer.MAX_VALUE);
        }
    }
    //求源点s到其他点的最短路径
    public static void dijkstra(int s){
        //false表示蓝点(未确定最短路径的带能),true表示白点(确定路径的点)
        Arrays.fill(vis,false);
        //默认情况下设置为无穷大
        Arrays.fill(dis,Integer.MAX_VALUE);
        dis[s]=0;   //自己到自己的距离是0
        while(true){
            int mini=0;
            int min_=Integer.MAX_VALUE;
            for (int j = 1; j <=n ; j++) {
                if(!vis[j]&&min_>dis[j]){//从蓝点触发找出最小的点
                    mini=j;
                    min_=dis[j];
                }
            }
            //如果没找到蓝点，说明结束
            if(mini==0){
                break;
            }
            vis[mini]=true; //将当前点mini设置为白点
            for (int i = 1; i <=n ; i++) {
                if(!vis[i] &&dis[i]>dis[mini]+mp[mini][i]){
                    dis[i]=dis[mini]+mp[mini][i];
                    pre[i]=mini;//设置i的前驱为mini
                }
            }
        }
    }
    //求到z的最短路径的路线
    public static void output(int z){
        if(z==0){
            return;
        }
        output(pre[z]);
        System.out.print(z+"->");
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n= scan.nextInt();
        m=scan.nextInt();
        mp=new int[n+1][n+1];
        dis=new int[n+1];
        vis=new boolean[n+1];
        pre=new int[n+1];
        initmp();   //刚开始都设置无穷大
        for (int i = 0; i <m ; i++) {
            //u到v的距离为w
            int u = scan.nextInt();
            int v = scan.nextInt();
            int w = scan.nextInt();
            if(mp[u][v]>w){
                mp[u][v]=mp[v][u]=w;    //无向图
            }
        }
        dijkstra(1);    //1为起始点
        //输出从皇宫到编号为1-N建筑的最短距离
        Arrays.stream(dis).skip(1).forEach(x->{
            System.out.print(x+" ");
        });
//        System.out.println();
//        //从起点出发到每一个点的最短路径如下：
//        for (int i = 1; i <=n ; i++) {
//            output(i);
//            System.out.println();
//        }

    }
}

这里输出dis数组的时候我们忽略了下标为0的位置，因为我们这里默认下标都是从1开始，方便理解和计算。