前言：
✌ 作者简介：游坦之 ✌
🏆 大学软件工程在读，希望学到真本领，经世致用 🏆
📫 如果文章知识点有错误的地方，请指正！和大家一起学习，一起进步👀
💬 人生格言：成好人，行好事，做儒猿💬
🔥 如果感觉博主的文章还不错的话，还请👍关注、点赞、收藏三连支持👍一下博主哦

🚗顺序查找

🌴基本知识

**顺序查找是按照序列原有顺序对数组进行遍历比较查询的基本查找算法。**简单的说，就是给我一个集合，我从头到尾依次拿出每个元素与我要找的元素进行比对，如果是，说明查找成功，如果不是，继续查找下一个元素。

由此可见，顺序查找的结束条件有两个，一是查找到了我要找的元素。二是整个集合遍历完成。

🌵举个栗子

如下面这个例子，在集合{10,5,7,14,20}里查找元素7

首先，元素7与集合内第一个元素10比较，发现不是。

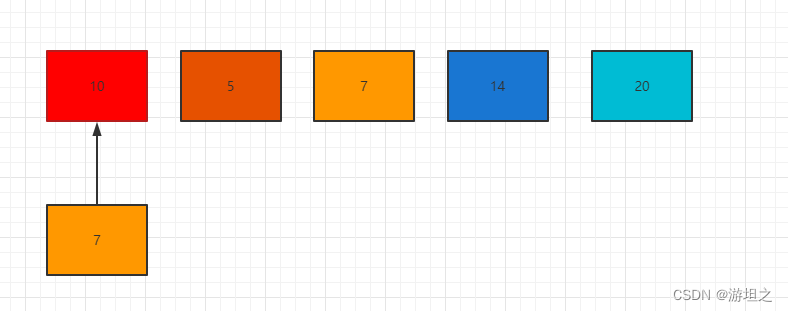
元素7继续与第二个元素5比较，发现也不是

元素7继续往后移动，与集合内第三个元素比较，发现是我们想要找的元素。

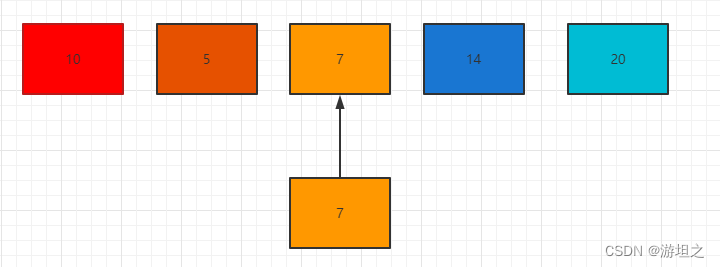
找到之后，输出元素在集合内的逻辑位置即3，因为数组中是从0开始的，所以7的真实位置是2，逻辑位置则需要加1。

由上面这个例子可以看出，顺序查找的时间效率是O（n），即如果在一千万个数据集，查找某一个元素，他的最差效果即是将全部的元素查找一遍。

🌾代码

实现代码如下：

for(int i=0;i<n;i++)
{
    if(a[i]==temp)
    {
        cout<<"逻辑位置为:"<<i+1<<endl;
        break;
    }
}

对于这样的集合来说，我们一般采用数组进行存储，其中最直接的原因在于数组简单快捷，且不需要其他高深的知识，只需要最基础的编程语法即可。除此之外，我们还可以采用其他的容器如：Set，Vector，Stack，Queue等等，只要是可以存储数据的容器，都可以实现顺序排序。

🌿什么样的题目适合顺序查找？

对于顺序查找而言，是一种最简单粗暴且没有任何技巧的查找方式。相较于有序的集合，顺序排序更适合于无序的集合。顺序排序适合小的数据集，因为对于计算机而言1s的计算量，大约在10的8次方，由于各种竞赛中，时间限制一般是在1s之内，所以一维的顺序查找，数据量在10的八次方，也就是一个亿的数据量，超过这个数据量的则无法用顺序查找的方式进行处理。

🚙折半查找

🍬基本知识

在计算机科学中，折半搜索，也称二分搜索、对数搜索，是一种在有序数组中查找某一特定元素的搜索算法。

搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

🍭举个栗子

举个例子：在集合{10,25,26,27,55,87,123,150,160}中查找元素27

首先，根据两端的序号计算中心点，即mid = (start + end) / 2 ; mid = (0+9) / 2 = 4,位于集合中且序号为4的元素是55（从0开始数），与27对比，27<55，这意味着27只可能在55的左侧出现（因为集合是有序的）。

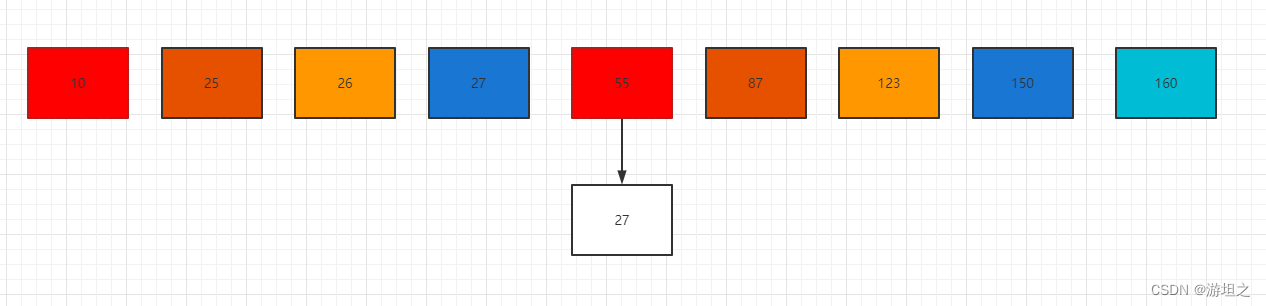
根据mid = (start + end) / 2；此时的end变成了原来mid，mid = (0+4)/2=2，拿出集合中序号为2的元素，即26，发现27>26，这意味着元素只可能在26的右侧。

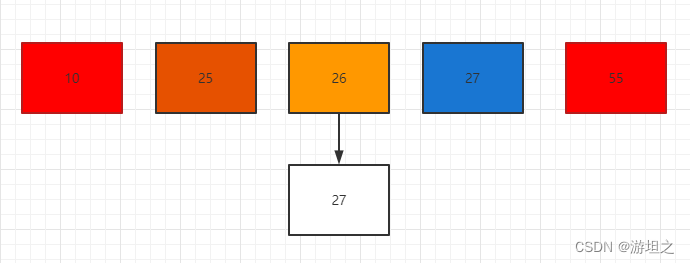
start更新为mid，此时的start为2，end为4，根据mid = (start+end)/2；计算得出mid为3，取出集合中序号为3的元素，是27。是我们要查找的元素，退出查找。

🍡代码

while(start<=end)
{
    int mid = (start+end)/2;
    if(a[mid]==temp)
    {
        cout<<"逻辑位置为:"<<mid+1<<endl;
        break;
    }else if(a[mid]<temp)
    {
        end = mid;
    }else if(a[mid]>temp)
    {
        start = mid;
    }
}

由上可知：折半查找退出的条件有两个，一是start比end大，二是查找到了想要查找的元素。

start和end的更新逻辑是，当现在拿到的元素a[mid]比要查找的元素temp小时，更新start为mid，当现在拿到的元素a[mid]比temp大时，更新end为mid；

折半查找的时间复杂度是O(log2n)，相较于顺序查找，折半查找的速度大大增强，但是折半查找只适合于有序的集合。对于有序的集合，set、map这样的容器也提供了相应的查找方式。有序集合和无序集合的其他查找方式则有待于我们的进一步深入学习。

✨ $\textcolor{blue}{原创不易，还希望各位大佬支持一下}$

👍 $\textcolor{green}{点赞，你的认可是我创作的动力！}$

⭐️ $\textcolor{green}{收藏，你的青睐是我努力的方向！}$

✏️ $\textcolor{green}{评论，你的意见是我进步的财富！}$