经典算法---索引查找
算法概念
任何被明确定义的计算过程可以称作算法,它将某个值活一组值作为输入,并产生莫格值或一组值作为输出。所以算法可以被称作将输入转为输出的一系列的计算步骤。
这样的概况是比较抽象和标准的,其实说白了就是步骤明确的解决问题的方法。由于是在计算机中执行,所以通常先用伪代码表示,清晰的表达出思路和步骤。这样真正执行的时候,就可以使用不同的语言来实现出相同的兄啊过给。
概况的说,算法就是解决问题的工具。在描述一个算法时,我们关注的是输入与输出。也就是说只要把原始数据和结果描述清楚了,那么算法所作的事情也就清楚了。
在设计一个算法时也是需要先明确我们有什么和我们要什么。

相关概念
数据结构
算法经常会和数据结构一起出现,这是因为对于同一个问题,使用不同的数据结构来存储数据,对应的算法可能千差万别。
所以在整个学习过程中,也会涉及到各种数据结构的使用
常见的数据结构包括:
- 数组
- 堆
- 栈
- 队列
- 链表
- 树等等
算法的效率
在一个算法设计完成后,还需要对算法的执行情况作一个评估。一个好的算法,可以大幅度的节省资源消耗和时间。在进行评估时不需要太具体,毕竟数据量是不确定的,通常是以数据量为基准确定一个量级。
通常会使用到两个概念:
- 时间复杂度
- 空间复杂度
时间复杂度
通常把算法中的基本操作重复执行的频度称为算法的时间复杂度。算法中的基本操作一般是指算法中最深层循环内的语句(赋值、判断、四则运算等基础操作)。我们可以把时间频度记为T(n),它与算法中语句的执行次数成正比。其中的n被称为问题的规模,大多数情况下为输入的数据量。
对于每一段代码,都可以转为常数或者与n相关的函数表达式,记作f(n)。如果我们把每一段代码的花费的时间加起来就能够得到一个刻画时间复杂度的表达式,在合并后保留量级最大的部分即可确定时间复杂度。
空间复杂度
程序从开始执行到结束所需要的内存量。也就是整个代码中最大需要占用多少的空间。为了评估算法本身,输入数据所占用的空间不会考虑,通常更关注运算时需要额外定义多少临时变量或多少存储结构。
元素查找介绍
查找也被称为检索,算法的主要目的是在某种数据结构中,找出满足给定条件的元素(以等值匹配为例)。如果找打满足条件的元素,则代表查找成功,否则查找失败。
在进行查找时,对于不同的数据结构以及元素集合状态,会有相对匹配的算法,在使用时也需要注意算法的前置条件。在元素查找相关文章中只讨论数据元素只有一个数据项的情况,即关键字(key)就是对应数据元素的值,对应到具体的数据结构,可以理解为一维数组。
-
顺序查找
也称为线性查找,是最简单的查找方法。思路也很简单,从数组的一边开始,逐个进行元素的比较,如果与给定的待查找元素相同,则查找成功,如果整个扫描结束后,仍未找到相匹配的元素,则查找失败。 -
折半查找
也称为二分查找,是一种效率相对较高的查找方法。使用该算法的前提要求是,元素已经有序,因为算法的核心思想是尽快的缩小搜索区间,这就需要保证在缩小范围的同时,不能有元素的遗漏。 -
索引查找
索引查找主要分为基本索引查找和分块查找,核心思想是对于无序的数据集合,先建立索引表,使得索引表有序或分块有序,结合顺序查找与索引查找的方法,完成查找。
基本索引查找
-
输入
主数据:n个数的序列,通常直接存放在数组中,可以是任何顺序。
基于主数据建立的索引表,索引表中的每个元素存储两个属性:关键字、主数据表中的序号,索引表按关键字有序。
待查找元素key -
输出
查找成功:返回元素所在位置的编号
查找失败:返回-1或自定义失败标识。 -
算法说明
基本索引查找是基于一个有序的索引表进行折半查找,然后再根据索引表与主数据表的关系确定数据所在位置的过程。所以只需要在折半查找后,从索引表中取出该元素在主数据集合中对应得位置即可。 -
算法流程
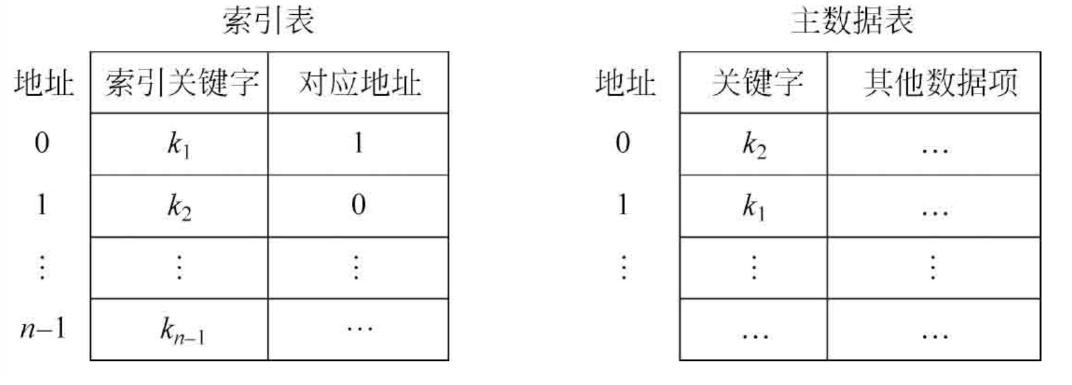
索引表得结构如下

1 索引表中的元素为关键字和地址两部分
2 关键字为从主数据表中提取出来的用于排序的属性,地址为主数据表中对应元素的位置。
3 在索引表中使用折半查找快速定位待查关键字位置
4 根据关联关系,提取出在主数据表中的对应位置
伪代码
使用T来表示索引表的集合,使用点来取出不同的属性(key为关键字,pos为对应地址)
left = 1
right = T.length
position = -1
while left <= right
mid = (left + right) / 2
if T[mid].key == key
position = mid
break
else if T[mid] > key
right = mid - 1
else
left = mid + 1
if position != -1
return T[position].pos
else
return -1
算法实践
- 输入数据
A = {11,34,20,10,12,35,41,32,43,14}
T = {10,3}, {11,0}, {12,4}, {14,9}, {20,2}, {32,7},{34,1},{35,5},{41,6},{43,8}
key = 41
java源码
public class BasicIndexSearch {
public static void main(String[] args) {
// 主数据表
int[] a = {11,34,20,10,12,35,41,32,43,14};
// 待查关键字
int key = 41;
// 使用排序算法或其他操作得到索引表
BasicTable[] t = {
new BasicTable(10,3),
new BasicTable(11,0),
new BasicTable(12,4),
new BasicTable(14,9),
new BasicTable(20,2),
new BasicTable(32,7),
new BasicTable(34,1),
new BasicTable(35,5),
new BasicTable(41,6),
new BasicTable(43,8)
};
// 调用算法,并输出结果
int result = search(t, key);
System.out.println(result);
}
private static int search(BasicTable[] t,int key){
// 初始化变量
int left = 0;
int right = t.length - 1;
int position = -1;
// 以下为二分查找算法
while (left <= right){
// 取中间元素,以下写法防止数据量较大时发生溢出
int mid = (right - left) / 2 + left;
if (t[mid].key == key){
// 此处直接使用mid
position = mid;
// 找到匹配的key后可提前跳出并结束循环
break;
}else if(t[mid].key > key){
right = mid - 1;
}else {
left = mid + 1;
}
}
if (position != -1){
// 返回对应的主数据表中的逻辑序号
return t[position].pos + 1;
}else {
// 未找到时返回-1
return -1;
}
}
}
// 定义索引表结构
class BasicTable{
public BasicTable(int key, int pos) {
this.key = key;
this.pos = pos;
}
int key;
int pos;
}
- 执行效果
7
- 点赞
- 收藏
- 关注作者


评论(0)