支持向量机 support vector machine
@[TOC](支持向量机 support vector machine)
1 概述
• 通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,即支持向量机的学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
• 上个世纪90年代,支持向量机获得全面发展,在实际应
用中,获得比较满意的效果,成为机器学习领域的标准
工具
2 常用的机器学习方法比较
• 概率分布的方法(经典的方法)
• Bayes方法, GMMs 用于复杂分布建模
• 决策树的方法(C4.5)
• 属性具有明确含义时使用,一种经典的方法
• 近邻分类
• 简单的方法,如果样本有代表性,维数不高时好用
• 支撑向量机
• 高维空间的小样本学习
• Boosting算法
• 大量训练样本下可以取得好的效果,速度很快
• 人工神经网络ANN
• 大量训练样本下可以取得好的效果,速度较慢
3 什么是SVM? 结构风险最小化
一个普通的SVM就是一条直线罢了,用来完美划分linearly separable的两类。但这又不是一条普通的直线,这是无数条可以分类的直线当中最完美的,因为它恰好在两个类的中间,距离两个类的点都一样远。
支持向量机就是 向量 支持 机(器)
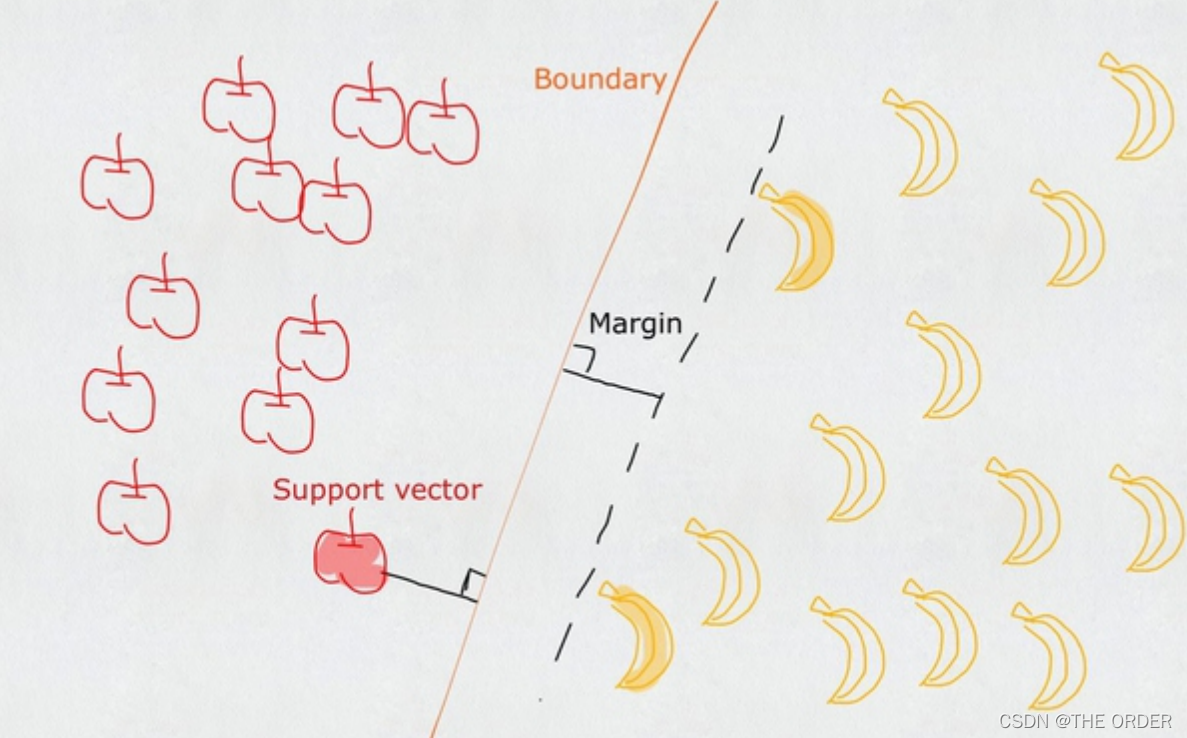
4 线性SVM
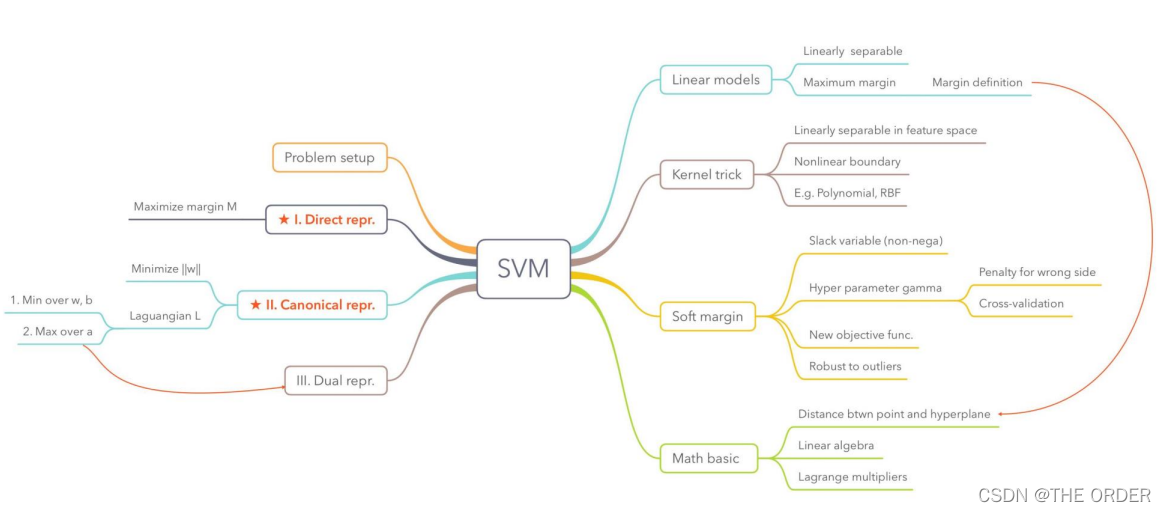
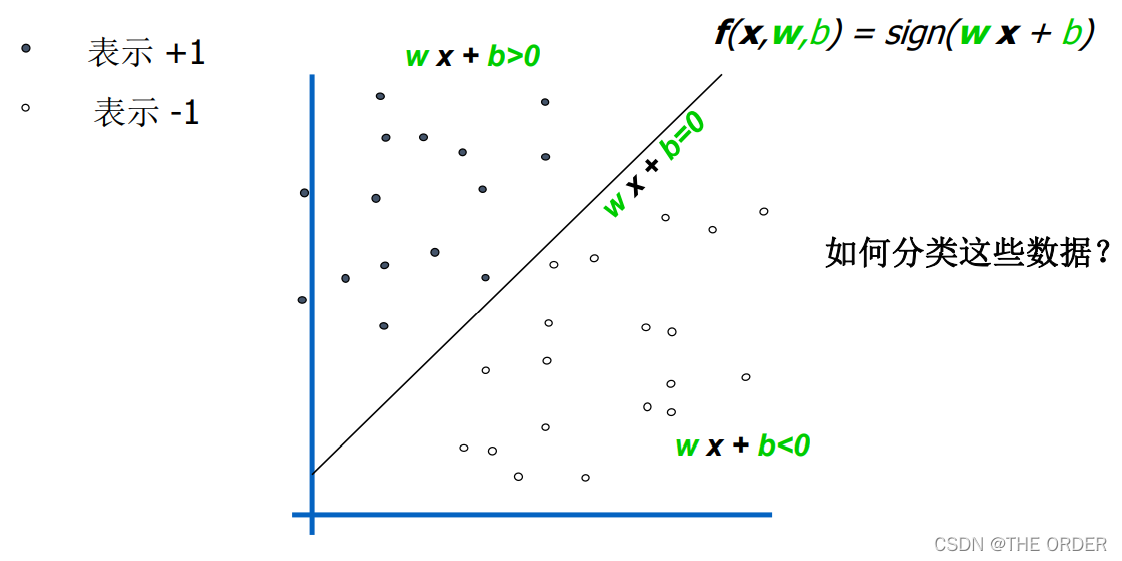
线性分类器解决的问题
根据一个带有类别标号的训练集合,通过学习一个线性分
类面,使得训练集合按照类别进行划分
通常转化成一个优化问题
以两类监督分类问题问题为例来解释
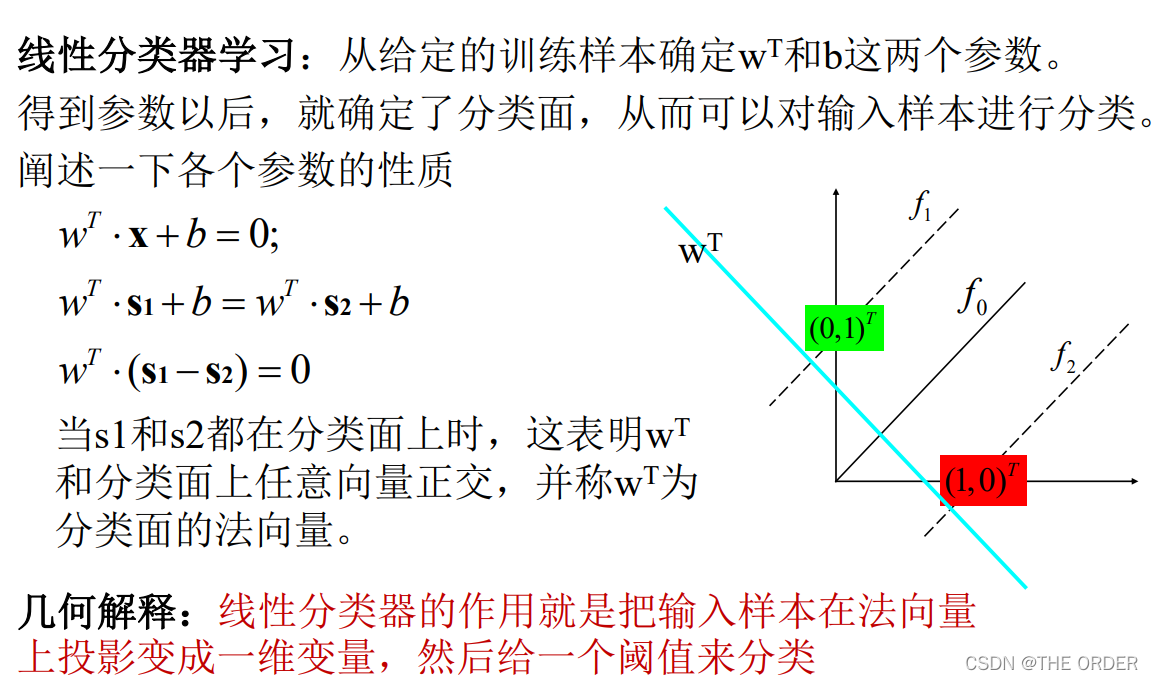
**分类面:**把一个空间按照类别切分两部分的平面,在二维空
间中,分类面相当于一条直线,三维空间中相当于一个平面,
高维空间为超平面
线性分类面函数形式为:
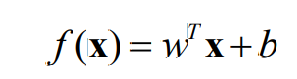
wT,b是分类面函数参数,x是输入的样本, wT权向量,b是偏移量
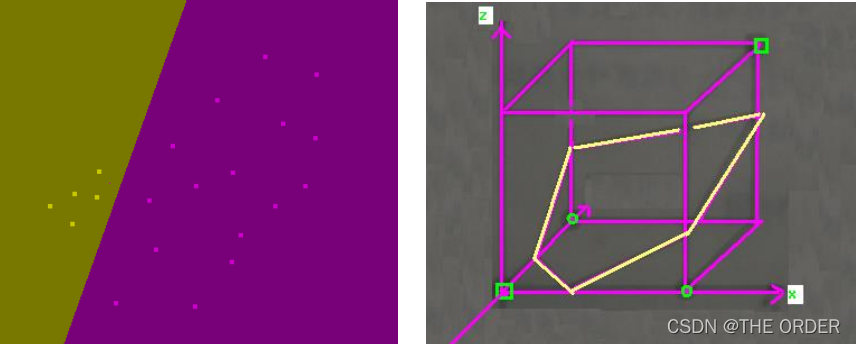



- 这种理论说明只有Margin上的样本点是
重要的,其他样本都不重要
Max-margin - 实践证明这种假设效果非常好.
• SVM从线性可分情况下的分类面发展而来
• Margin最大化分类面不仅仅要求经验风险尽可能的小,且使分类间隔最大
• SVM考虑寻找一个满足分类要求的分类面
• 过两类样本中离分类面最近的点且平行于分类面的训练样本就叫做支持向量
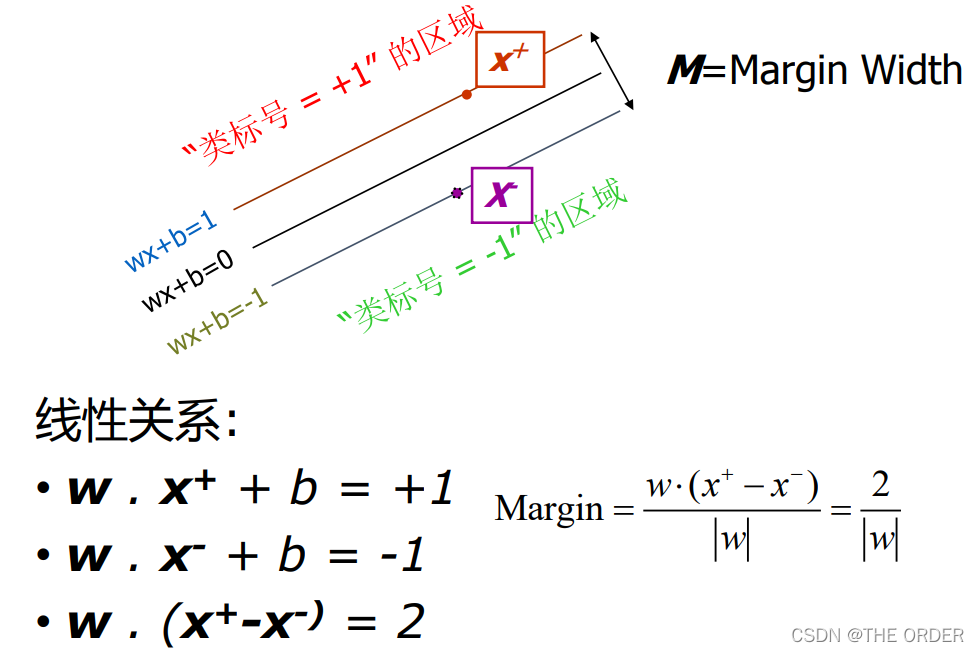


理解 Classification Margin
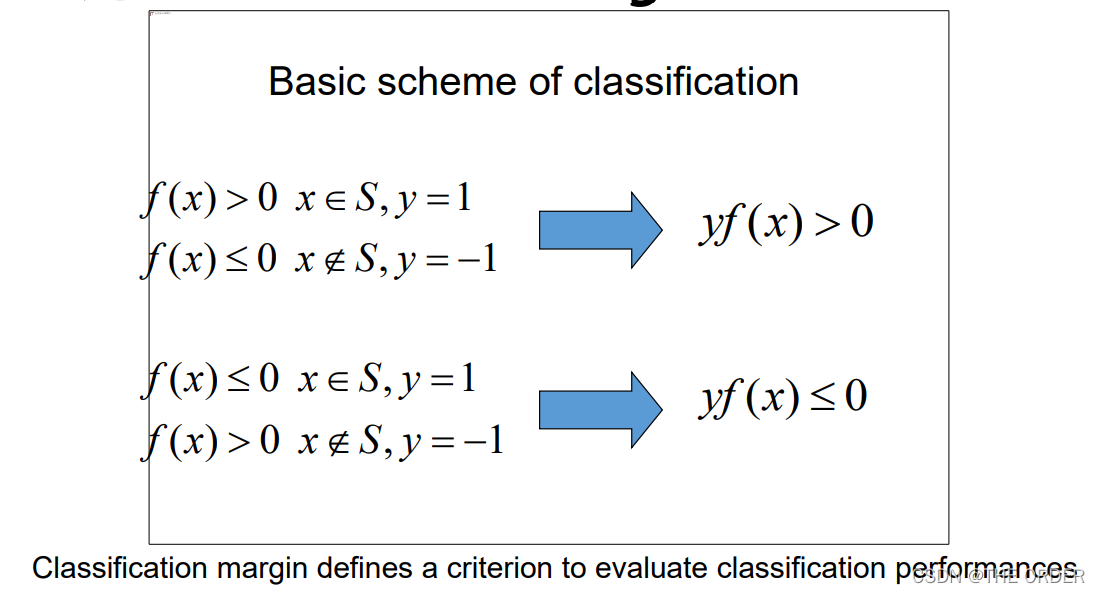
线性SVM求解

5 Lagrange函数优化问题
1629年,Lagrange最初是为了解决等式约束的最优化解
1951年,Kuhn和Tucker进一步把这个方法扩展到具有不等式约束的情况下,而他们理论实际基于Karush的工作。
通过对偶理论简化约束条件即Karush-Kuhn-Tucker互补条件解决了支持向量机的优化问题
Solving the Optimization Problem
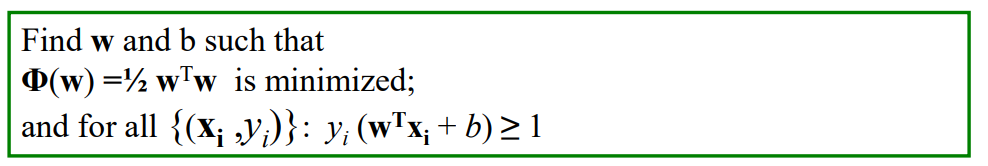
It is called the primal problem
Lagrange multipliers and KKT theorem

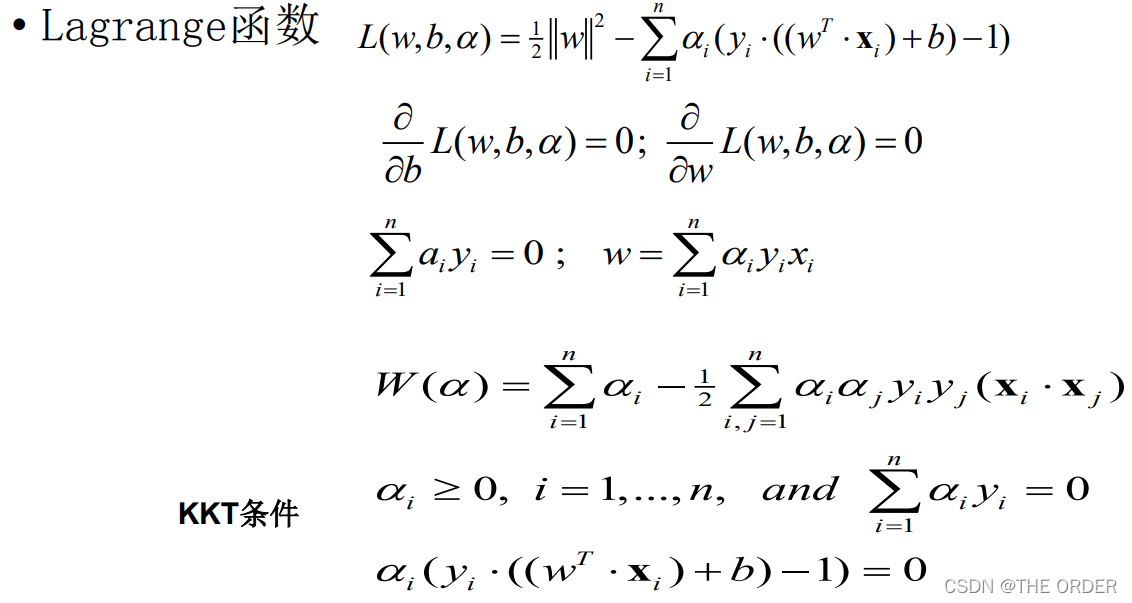
lagrange可以解决带约束条件不等式的最值问题,这里笔者用一个题目用lagrange求值
用 lagrange求解
已知4x^2+y^2+xy=1,求2x+y的最大值
L(x,y,λ)=2x+y-λ(4x^2+y^2+xy-1) λ是lagerange系数
建立lagrange方程组求偏导
L(x)=2-λx-λy=0
L(y)=1-2λy-λx=0
L(λ)=4x^2+y^2+xy-1=0
解得 x=(10^1/2)/10
y=(10^1/2)/5
λ=(10^1/2)/5
当x=(10^1/2)/10 y=(10^1/2)/5 时
2x+y的最大值为2(10^1/2)/10
6 Linear SVM 小结


7 处理线性不可分的情况
软间隔—线性SVM不完全可分情况
Kernel SVM—非线性SVM

Dataset with noise

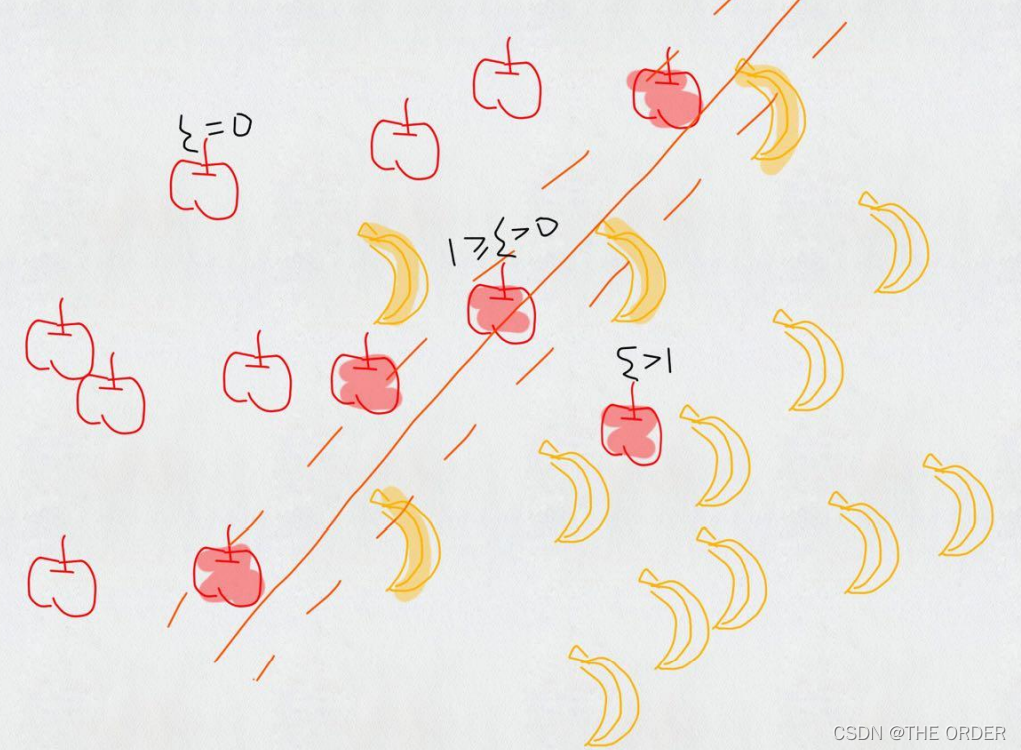
Soft Margin Classification

线性SVM求解:软间隔
最优化问题
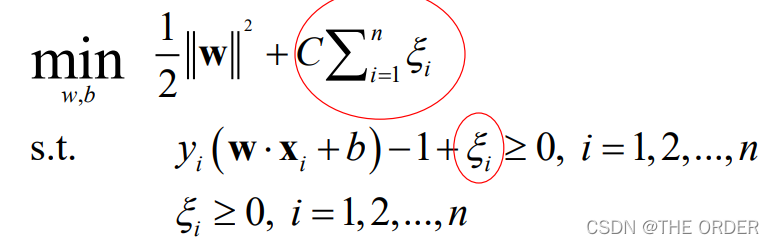



8 软间隔小结
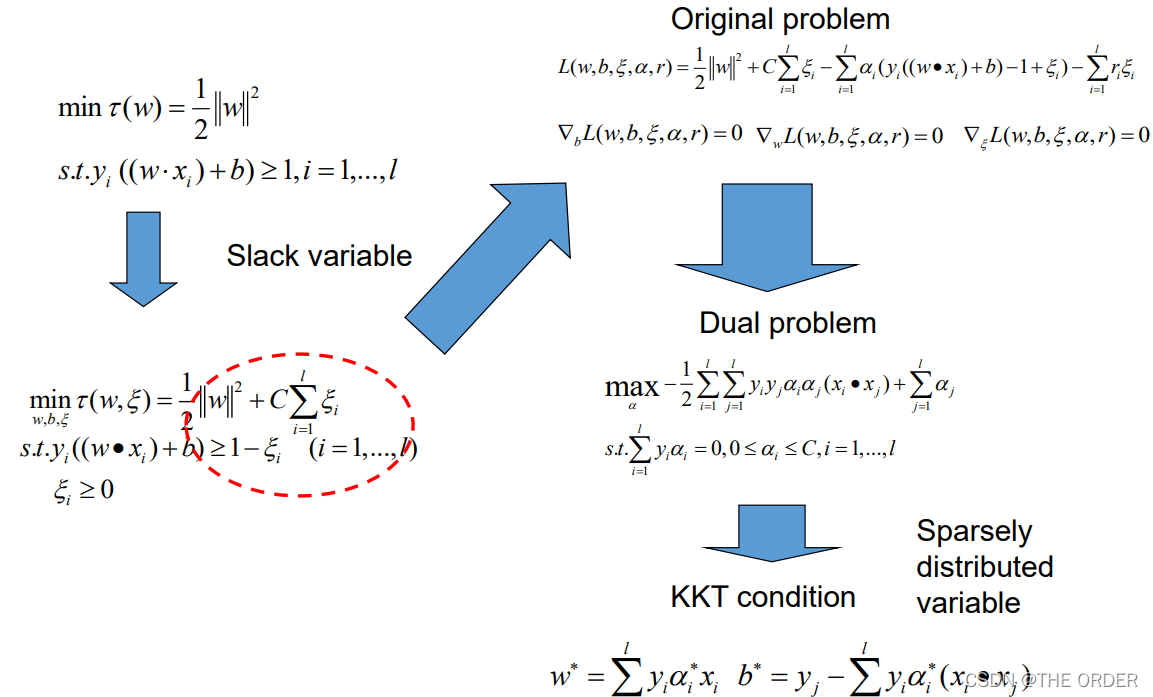
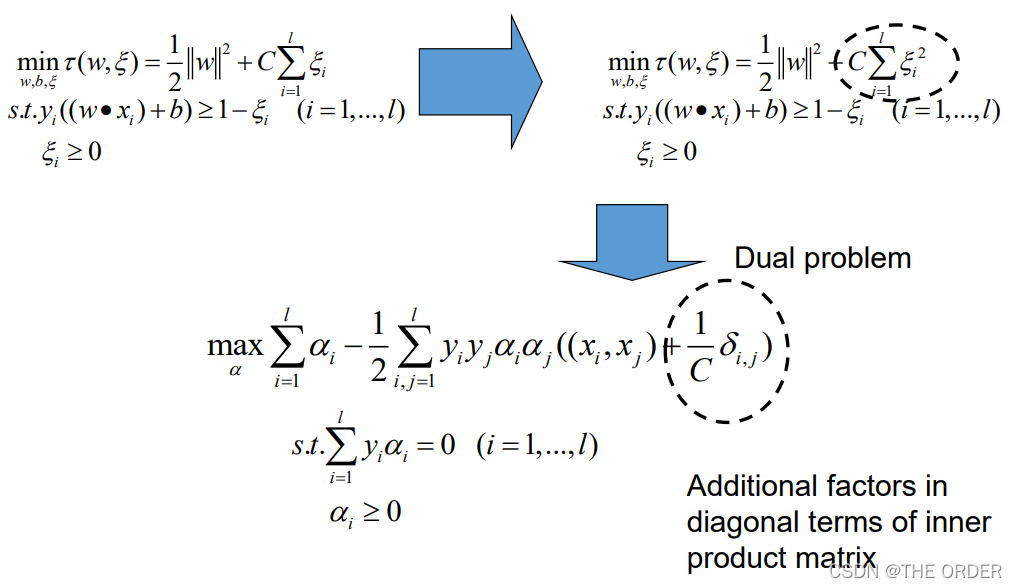
Hard Margin v.s. Soft Margin


9 非线性SVM
Non-linear SVMs
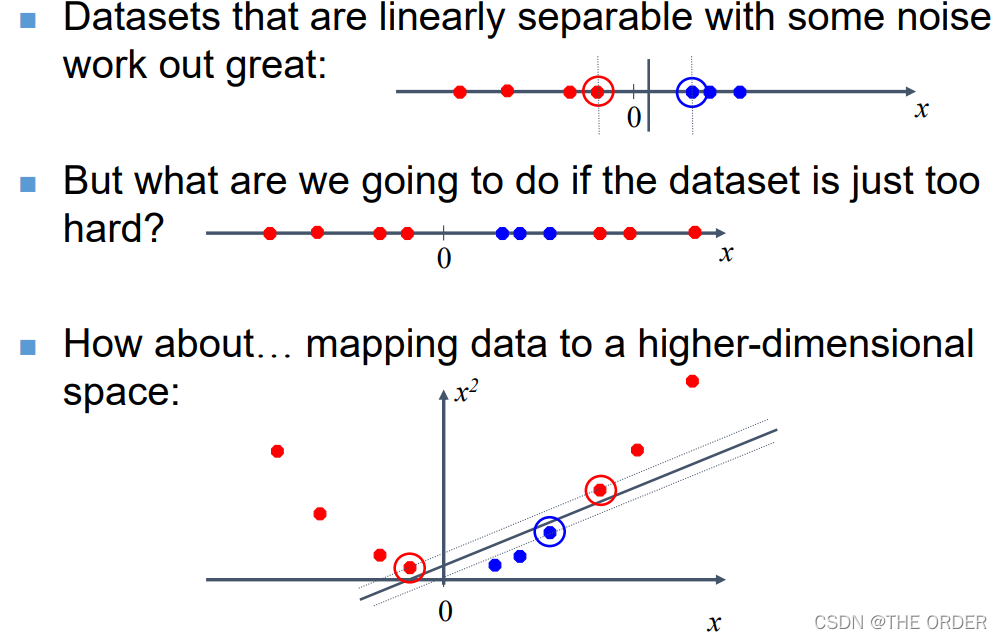
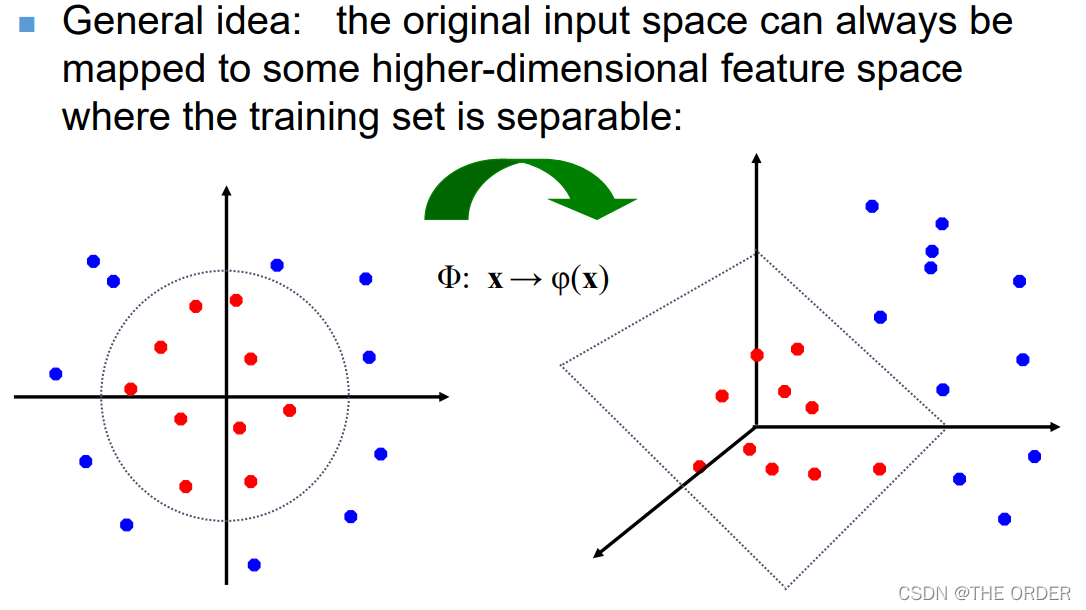
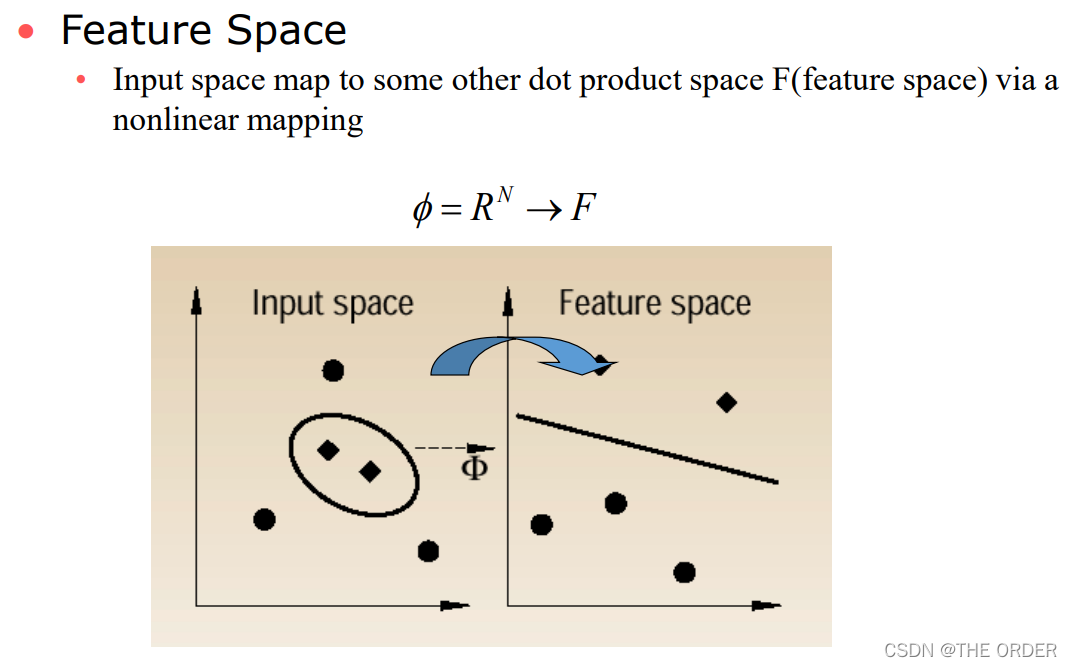
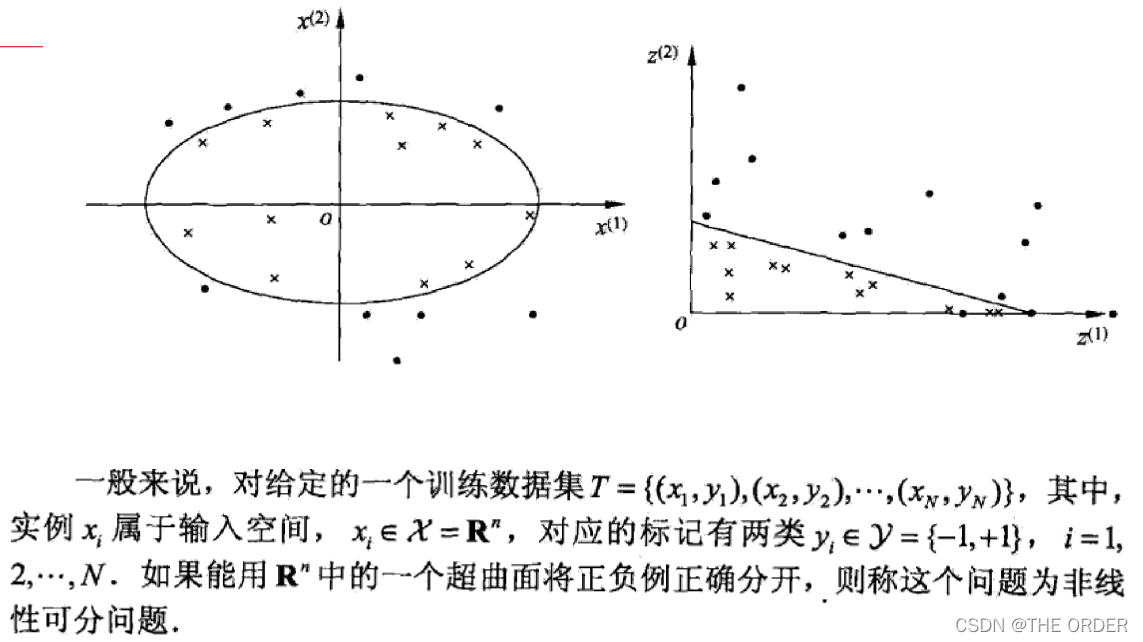
思路:非线性问题变为线性问题。
• 如何操作?
• 寻找非线性变换函数,也即kernel trick
关于核函数,博主太弱了,暂时无法解释清楚
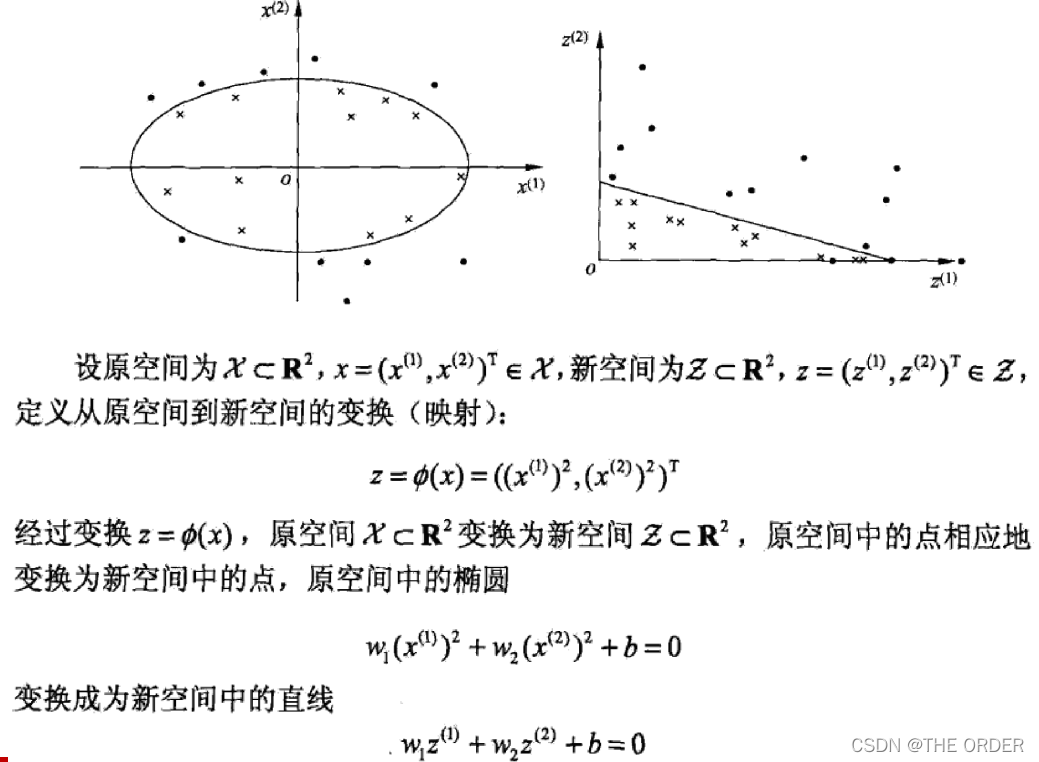
什么样的函数可以做核函数?
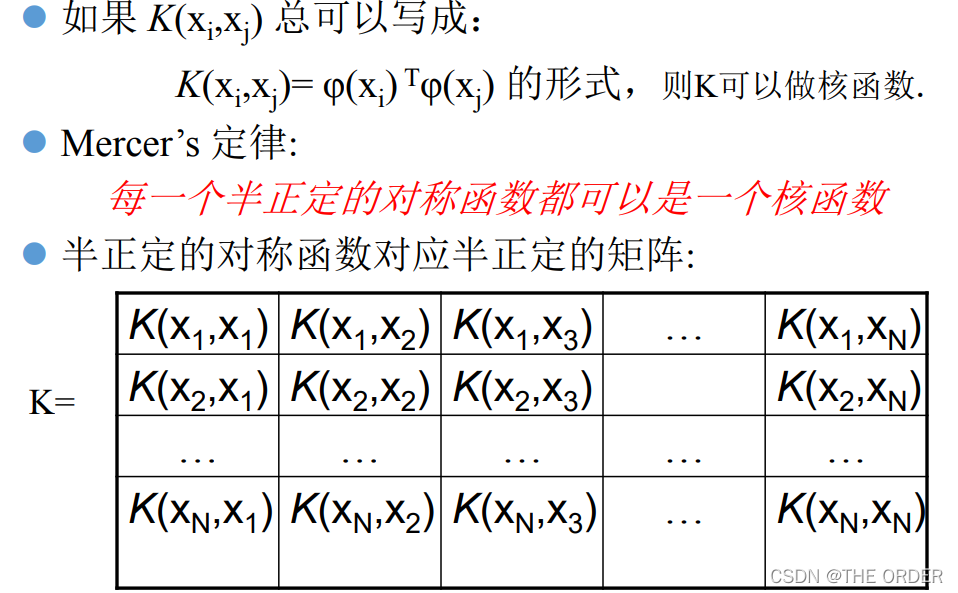
核函数举例
线性分类器的运算是内积运算


Kernel SVMs 求解

Kernel trick小结: A nonlinear solver


10 SVM训练算法-SMO
算法流程:每次选取两个α进行更新
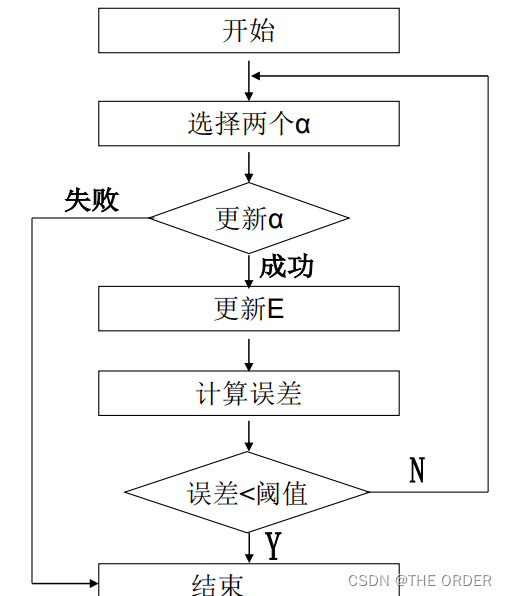
最后得到迭代公式:
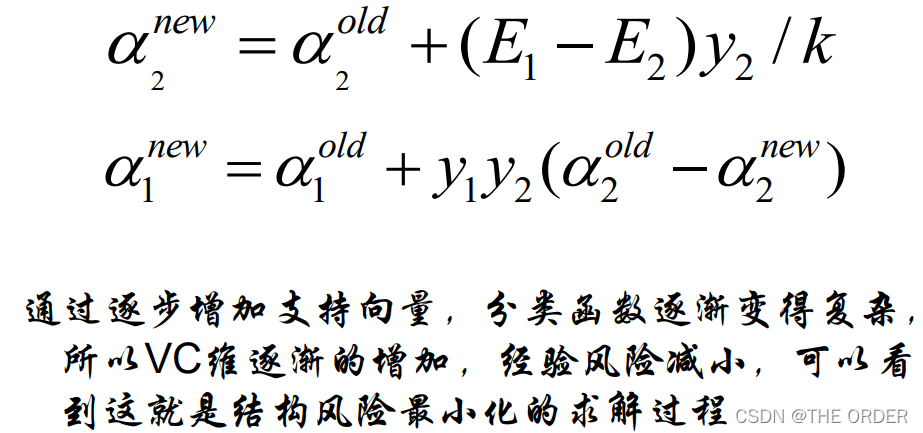
- 点赞
- 收藏
- 关注作者


评论(0)