数据分析python PCA主成分分析
【摘要】 数据分析python PCA主成分分析
在有许多变量的情况下,主成分分析可以使得我们最大程度的保留住重要信息来训练模型,运行环境是anconda 3.8,jupter notebook
1初始准备
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
import matplotlib.pyplot as pl
from sklearn.datasets import load_wine
from sklearn.pipeline import make_pipeline
pl.rcParams['font.sans-serif']='SimHei' #画图正常显示中文
pl.rcParams['axes.unicode_minus']=False #决绝保存图像是负号‘-’显示方块的问题
%matplotlib inline
2 读出数据与分组
features,target=load_wine(return_X_y=True)#三分类的酒数据集
features.shape,target.shape
RANDOM_STATE=42 #随机,类似随机种子seed
#将数据切分成7:3分制成训练集和测试集
X_train,X_test,y_train,y_test=train_test_split(features,target,test_size=0.30,random_state=RANDOM_STATE)
3 对不使用PCA,使用PCA不做标准化,使用PCA标准化三种情况进行分组
#不使用PCA
raw_clf=make_pipeline(StandardScaler(),LogisticRegression())
raw_clf.fit(X_train,y_train)
pred_test_raw=raw_clf.predict(X_test)
#使用PCA但不做数据处理
unscaled_clf=make_pipeline(PCA(n_components=2),LogisticRegression())
unscaled_clf.fit(X_train,y_train)
pred_test=unscaled_clf.predict(X_test)
#使用PCA,同时做数据处理
std_clf=make_pipeline(StandardScaler(),PCA(n_components=2),LogisticRegression())
std_clf.fit(X_train,y_train)
pred_test_std=std_clf.predict(X_test)
#查看各种情况下的分类准确率
print(u'\n不使用PCA,预测准确率','{:.2%}'.format(metrics.accuracy_score(y_test,pred_test_raw)))
print(u'\n使用PCA,未标准化预测准确率','{:.2%}'.format(metrics.accuracy_score(y_test,pred_test)))
print(u'\n使用PCA,标准化预测准确率','{:.2%}'.format(metrics.accuracy_score(y_test,pred_test_std)))
对三种情况进行正确率比较

4 将抽取出来的主成分进行展示
#将pca信息抽取出来
pca=unscaled_clf.named_steps['pca']
pca_std=std_clf.named_steps['pca']
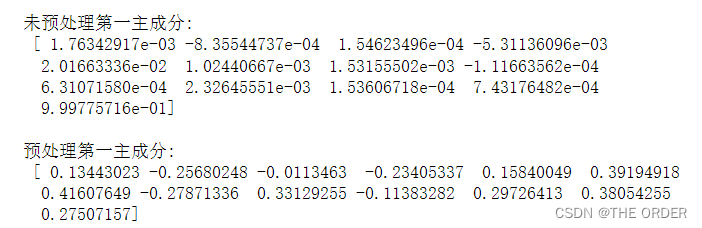
#打印最主要的主成分,注意,它是特征空间中的主成分轴,表达了数据中具有最大方差的方向
print(u'\n未预处理第一主成分:\n',pca.components_[0])
print(u'\n预处理第一主成分:\n',pca_std.components_[0])
5 将PCA分类结果画图
#对训练集数据进行PCA降维以备绘图
X_train_nostd=pca.transform(X_train)
scaler=std_clf.named_steps['standardscaler']
X_train_std=pca_std.transform(scaler.transform(X_train))
FIG_SIZE=(10,7)
fig,(ax1,ax2)=pl.subplots(ncols=2,figsize=FIG_SIZE)
#不预处理的PCA
for l,c,m in zip(range(0,3),('blue','red','green'),('^','s','o')):
ax1.scatter(X_train_nostd[y_train==l,0],X_train_nostd[y_train==l,1],
color=c,
label='class %s'% l,
alpha=0.5,
marker=m)
#预处理后的PCA
for l,c,m in zip(range(0,3),('blue','red','green'),('^','s','o')):
ax2.scatter(X_train_std[y_train==l,0],X_train_std[y_train==l,1],
color=c,
label='class %s'% l ,
alpha=0.5,
marker=m)
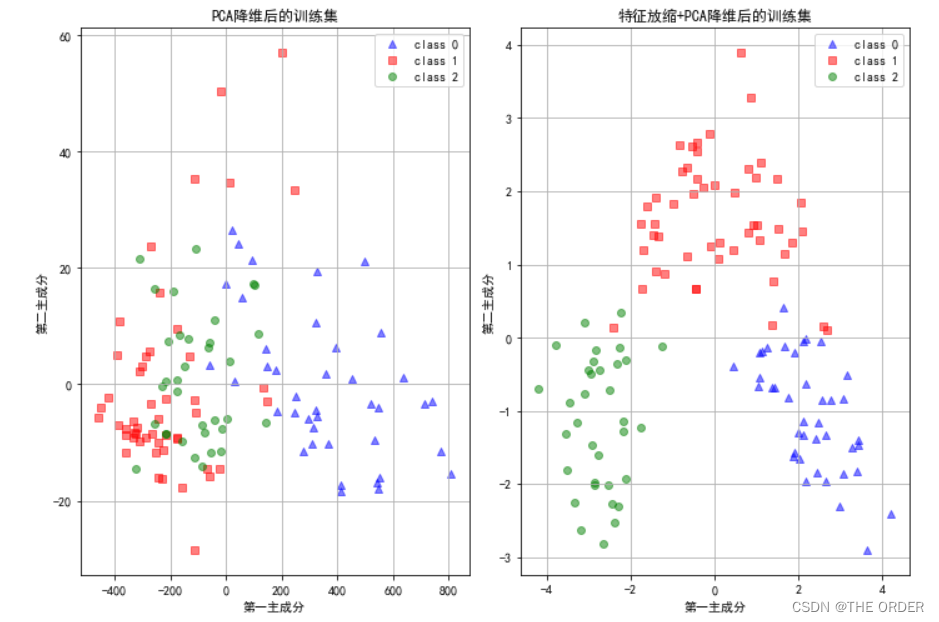
ax1.set_title(u'PCA降维后的训练集')
ax2.set_title(u'特征放缩+PCA降维后的训练集')
for ax in (ax1,ax2):
ax.set_xlabel(u'第一主成分')
ax.set_ylabel(u'第二主成分')
ax.legend(loc='upper right')
ax.grid()
pl.tight_layout()
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)