1.why学

离散的含义是指不同的连接在一起的元素，主要是研究基于离散量的结构和相互间的关系，其对象一般是有限个或可数个元素。
离散数学是【数学】和【计算机】的桥梁，其最重要的内容是数论和图论。

数学本质——抽象；
计算机本质——算法（是抽象的一种）。

一般人学算法则够用，但是如果将算法“抽象”到理论高度，如将DFS、dijstra算法等进行证明算法正确性、有效性、局限性，就需要学离散数学。

（1）实际应用

如正则表达式（练习网站RegexOne：https://regexone.com/）

（2）应试重点

在知乎上看到国内外大学学习的重点对比图：

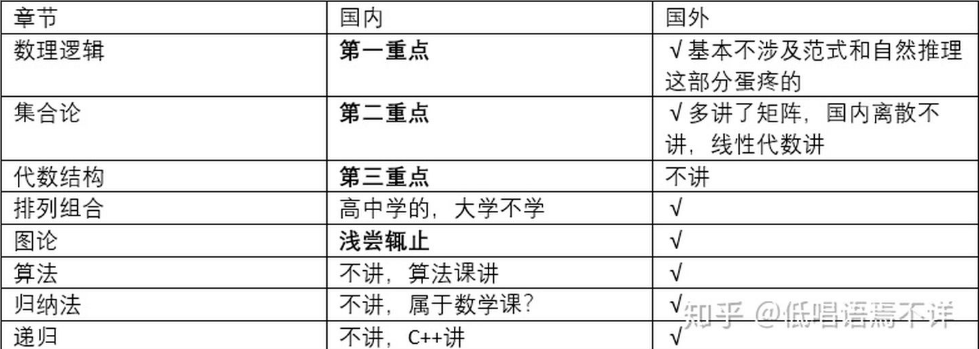
2.笔记/概念

1.关系的性质

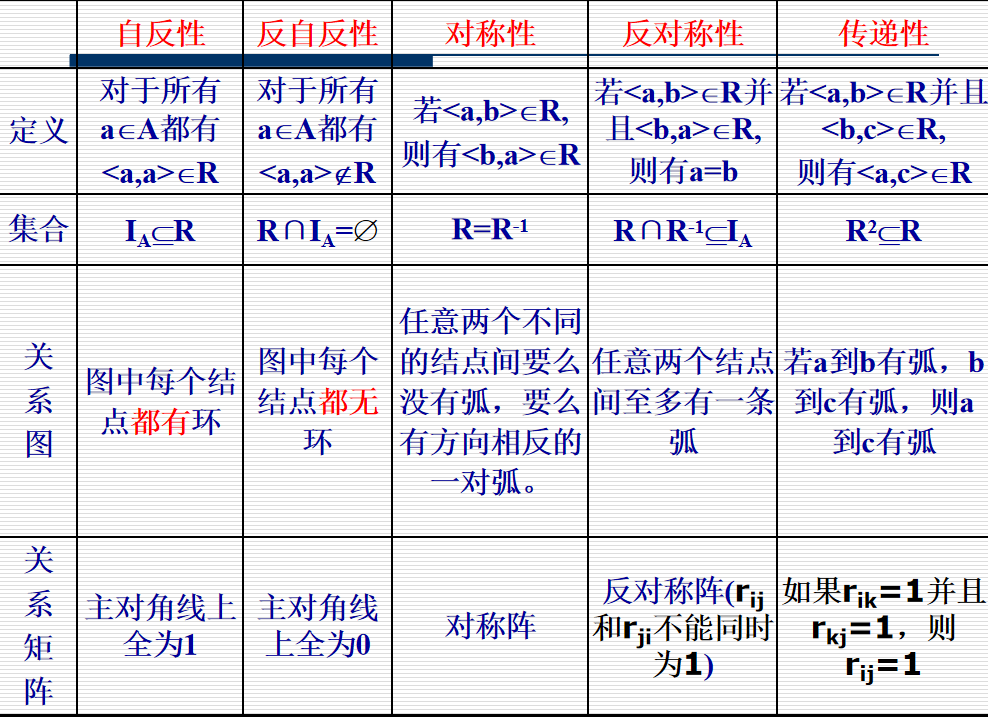
注意：存在既不是自反，也不是反自反的关系；空集满足反自反关系。

2.等价关系

关系R是若是等价关系，则R的关系图中，关系矩阵被分成了不同的块——类似连通分量。

3.谓词公式分类

（1）永真/重言
（2）可满足式
——至少存在一组解释使得谓词的真值为真；
（3）矛盾式/永假式/不可满足式

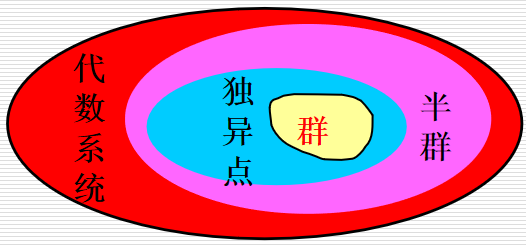
4.群、半群、独立点

5.欧拉图和哈密顿图

（1）欧拉图：有欧拉回路（每条边经过1次，其中回路是可以重复个相同点的）。
——判定方法：无奇数度数的结点。

欧拉通路：有0或2个奇数度。
PS：欧拉通路即每条边通过一次。

（2）哈密顿图：有哈密顿回路（每个点经过1次）。
——判定方法：所有结点的度都大于等于n/2，n为图的结点个数（即阶数）。

（3）二部图：
——判定方法：图中所有回路的长度均为偶数。

（4）平面图：重画后能避免一些边在非结点处有交叉。
——判定方法：若边数大于1，则平面图满足：边数 ≤ 3*结点数-6。

6.左陪集

题目描述：
设 <Z6,+6> 是一个群，这里 +6 是模 6 加法， Z6={0 ， 1 ， 2 ， 3 ， 4 ， 5} ，试求出 <Z6,+6> 的所有子群及其相应左陪集。

解答：
由于循环群的子群是循环群,并且群的阶的每一个正因子存在唯一的子群。
即子群的阶是6的正因子，6的正因子只有1,2,3,6,因此Z6共有4个子群,
它们分别是一阶子群，2阶子群，3阶子群，6阶子群 =Z6（本身）。
子群首先有两个平凡子群，即{[0]}，{Z6}。一个为幺元，另一个为群本身。
然后考虑 [2] 生成的子群: {[0],[2],[4]}
然后考虑 [3] 生成的子群: {[0],[3]}
所以子群<{[0]},+6>,<{[0],[3]}，+6>,<{[0],[2],[4],+6}>，<{Z6,},+6>

下面求出左陪集：
分别用{Z6}中的每一个元素 加上 下面的集合，即可得：

{[0]}的左陪集：{[0]},{[1]},{[2]},{[3]},{[4]},{[5]}.
{[0],[3]}的左陪集：{[0],[3]},{[1],[4]},{[2],[5]}.
{[0],[2],[4]}的左陪集：{[0],[2],[4]},{[1],[3],[5]}.
{[Z6]}的左陪集：{[0],[1],[2],[3],[4],[5]}.(Z6本身)

那么，为什么<{[0],[1],[5]}>不是子群？

根据子群的定义，条件之一：任意两元素的运算结果仍在子群中，即封闭性。
那么可以取两个元素[1]，[1],模加6结果（1+1）%6=2，元素[2]并不在<{[0],[1],[5]}>中，同理验证元素[5]。故其不是子群。

举例：
H的左陪集应该是对所有a属于G，应该是使a*h结果相等的集合。
比如：H={[0],[2]}是<z4,+4>的子群，H的左陪集为[0]+H={[0],[2]} ; [1]+H={[1],[3]}; [2]+H={[2],[0]}; [3]+H={[1],[3]};
可以看出[0]+H={[0],[2]}与[2]+H={[2],[0]}相等，其中一个左陪集为{[0],[2]};同理，另外一个左陪集为{[1],[3]};
右陪集也一样。

6.概念汇总

3.思维导图

reference

（1）上图中的离散数学思维导图源自https://blog.csdn.net/lwj3326/article/details/106180528。
（2）git/SQL/正则表达式的在线练习网站
（3）笔记部分源自这里
（4）https://blog.csdn.net/guanripeng/article/details/105908983

文章来源: andyguo.blog.csdn.net，作者：山顶夕景，版权归原作者所有，如需转载，请联系作者。

原文链接：andyguo.blog.csdn.net/article/details/114265038