📢📢📢📣📣📣
🌻🌻🌻Hello，大家好我叫是Dream呀，一个有趣的Python博主，小白一枚，多多关照😜😜😜
🏅🏅🏅CSDN Python领域新星创作者，大二在读，欢迎大家找我合作学习
💕入门须知：这片乐园从不缺乏天才，努力才是你的最终入场券！🚀🚀🚀
💓最后，愿我们都能在看不到的地方闪闪发光，一起加油进步🍺🍺🍺
🍉🍉🍉“一万次悲伤，依然会有Dream，我一直在最温暖的地方等你”，唱的就是我！哈哈哈~🌈🌈🌈
🌟🌟🌟✨✨✨

@TOC

9.1背包问题

假设你是个小偷，背着一个可装4 磅东西的背包。

你可盗窃的商品有如下3 件：

音响，3000美元，4磅

笔记本电脑，2000美元，3磅

吉他，1500美元，1磅

每个动态规划算法都从一个网格开始，背包问题的网格如：

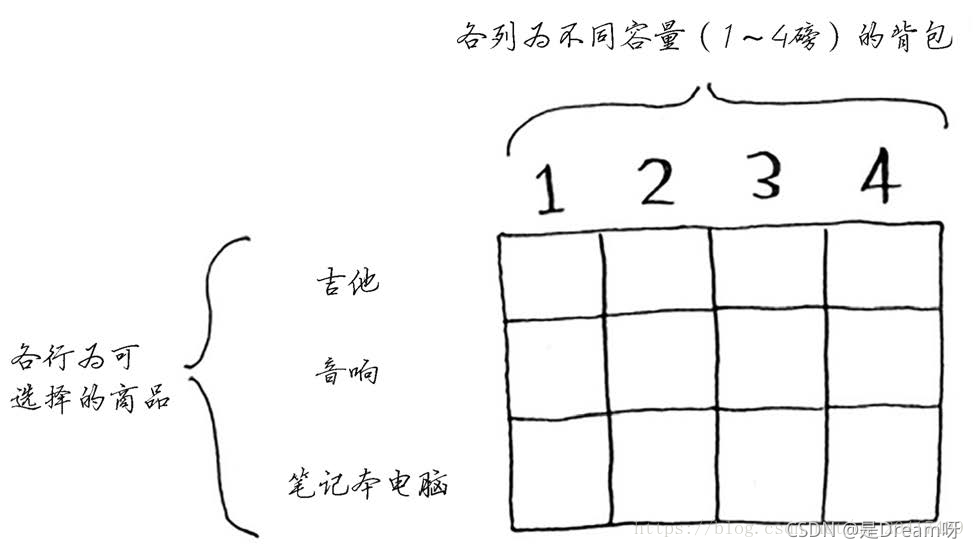
最终结果：


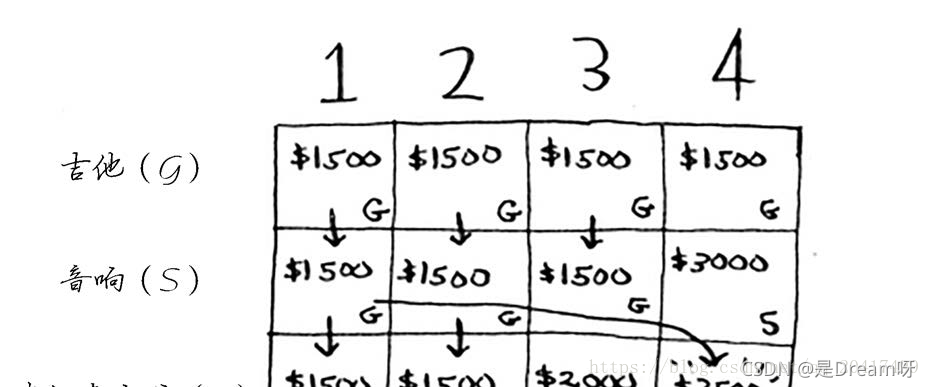
动态规划功能强大，它能够解决子问题并使用这些答案来解决大问题。但仅当每个子问题都是离散的，即不依赖于其他子问题时，动态规划才管用。
最优解可能导致背包没装满。

9.2 动态规划

动态规划先解决子问题，再逐步解决大问题。
对于背包问题，你先解决小背包（子背包）问题，再逐步解决原来的问题。
每个动态规划算法都从一个网格开始，网格的各行为商品，各列为不同容量（ 1～4磅）的背包。所有这些列你都需要，因为它们将帮助你计算子背包的价值。
动态规划可帮助你在给定约束条件下找到最优解。在背包问题中，你必须在背包容量给定的情况下，偷到价值最高的商品。
在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。要设计出动态规划解决方案可能很难，这正是本节要介绍的。下面是一些通用的小贴士。
每种动态规划解决方案都涉及网格。

9.3 绘制网格

对于前面的背包问题，最终答案总是在最后的单元格中。但对于最长公共子串问题，答案为网格中最大的数字——它可能并不位于最后的单元格中。

9.4 小结

1. 需要在给定约束条件下优化某种指标时，动态规划很有用。
2. 问题可分解为离散子问题时，可使用动态规划来解决。
3. 每种动态规划解决方案都涉及网格。
4. 单元格中的值通常就是你要优化的值。
5. 每个单元格都是一个子问题，因此你需要考虑如何将问题分解为子问题。
6. 没有放之四海皆准的计算动态规划解决方案的公式。

好啦，这就是今天要给大家分享的全部内容了
如果你喜欢的话，就不要吝惜你的一键三连了~