多元线性回归分析问题

什么是多元线性回归

在回归分析中，如果有两个或两个以上的自变量，就称为多元回归。**事实上，一种现象常常是与多个因素相联系的，由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。**因此多元线性回归比一元线性回归的实用意义更大。

y=β0＋β１x1+β2x2+ … +βpxp+ε # 公式

今天讲一个例子

这里有个excel 文件数据，我们来研究到底是哪个因素影响sales最明显，是TV，还是radio，还是newspaper，也就是找的销售额到底是那家个元素引起的，怎么才能提高销售额？

导入相对的库

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('ggplot')   #使用ggplot样式
from sklearn.linear_model import LinearRegression  # 导入线性回归
from sklearn.model_selection import train_test_split  # 训练数据
from sklearn.metrics import mean_squared_error  #用来计算距离平方误差，评价模型

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
 

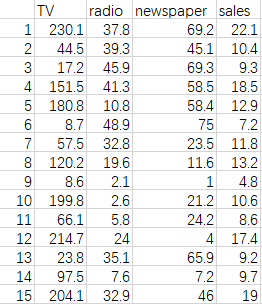
打开文件

data = pd.read_csv('Advertising.csv')
data.head()  #看下data

  

 

  
1
  
2
 

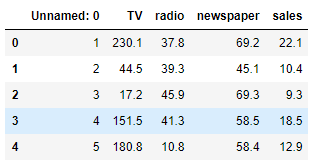
先画图分析一下

plt.scatter(data.TV, data.sales)

  

 

  
1
 

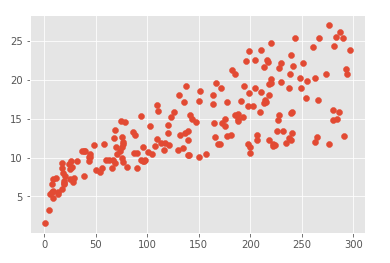
plt.scatter(data.radio, data.sales)

  

 

  
1
 

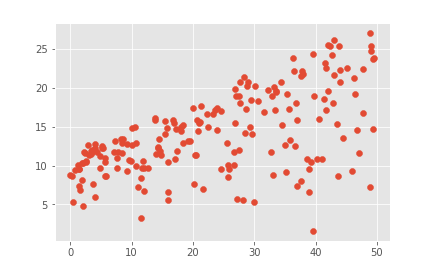
plt.scatter(data.newspaper, data.sales)

  

 

  
1
 

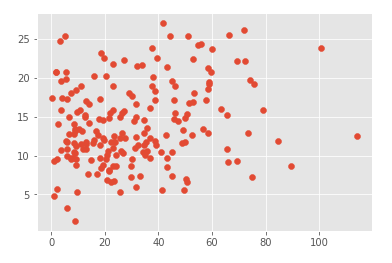
从图中分析看出newspaper的点分散太广，预测毫无关系，应该要去除

进入代码环节

x = data[['TV','radio','newspaper']]
y = data.sales
x_train,x_test,y_train,y_test = train_test_split(x, y)  #得到训练和测试训练集
model = LinearRegression()  #导入线性回归
model.fit(x_train, y_train)  # 
model.coef_ # 斜率 有三个
model.intercept_  # 截距

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
 

得到

array([ 0.04480311,  0.19277245, -0.00301245])
3.0258997429585506

  

 

  
1
  
2
 

for i in zip(x_train.columns, model.coef_): print(i) #打印对应的参数

  

 

  
1
  
2
 

('TV', 0.04480311217789182)
('radio', 0.19277245418149513)
('newspaper', -0.003012450368706149)

  

 

  
1
  
2
  
3
 

mean_squared_error(model.predict(x_test), y_test)  # 模型的好坏用距离的平方和计算

  

 

  
1
 

4.330748450267551

  

 

  
1
 

y =0.04480311217789182 * x1 + 0.19277245418149513 *x2 -0.003012450368706149 * x3 + 3.0258997429585506

我们可以看到newspaper的的系数小于0，说明了投入了，反而影响销售额 那么如何改进模型，就是去掉newspaper的数值

x = data[['TV','radio']]
y = data.sales
x_train,x_test,y_train,y_test = train_test_split(x, y)
model2 = LinearRegression()
model2.fit(x_train,y_train)
model2.coef_
model2.intercept_
mean_squared_error(model2.predict(x_test),y_test)

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
 

array([0.04666856, 0.17769367])
3.1183329992288478
2.984535789030915  # 比第一个model的小，说明更好

  

 

  
1
  
2
  
3
 

y =0.04666856 * x1 +0.17769367 *x2 + 3.1183329992288478

文章来源: maoli.blog.csdn.net，作者：刘润森！，版权归原作者所有，如需转载，请联系作者。

原文链接：maoli.blog.csdn.net/article/details/105286185