单调栈是一种特殊的栈数据结构，通常用于解决与数组相关的一些问题，尤其是那些涉及到寻找下一个更大（或更小）元素的问题。单调栈的基本思想是通过维护一个单调的顺序（递增或递减）来高效地推导出结果。

单调栈的主要特点

1. 单调性：栈中的元素保持单调递增或递减。根据问题的需要，我们可以选择是维护一个单调递增栈还是单调递减栈。

   • 单调递增栈：栈底到栈顶的元素从小到大排列。
   • 单调递减栈：栈底到栈顶的元素从大到小排列。

2. 高效性：使用单调栈可以在O(n)的时间复杂度内解决一些复杂度较高的问题，而传统方法可能需要O(n^2)的时间复杂度。

单调栈的应用场景

1. 下一个更大元素：给定一个数组，找出每个元素右边第一个比它大的元素。

2. 下一个更小元素：与下一个更大元素类似，只不过寻找的是比当前元素小的元素。

3. 柱状图中矩形的最大面积：求解给定柱状图中可以形成的最大矩形面积。

单调栈的基本操作

以下是单调栈的基本操作步骤：

1. 初始化一个空栈。

2. 遍历数组中的每个元素，做如下操作：

   • 当栈不为空且当前元素与栈顶元素的关系不满足单调性（对于递增栈，当前元素大于栈顶元素），那么可以进行弹栈操作。
   • 弹出栈顶元素并记录结果（或执行对应的操作），直到栈为空或栈顶元素满足单调性。
   • 将当前元素压入栈中。

3. 遍历结束后，栈中可能还有一些元素，这些元素的结果可能需要特殊处理（例如，找不到下一个元素时的默认值）。

OK，话不多说，直接上题：

503.下一个更大元素II 【中等】

题目：

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

示例 1:

输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

示例 2:

输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]

提示:

• 1 <= nums.length <= 10**4
• -10**9 <= nums[i] <= 10**9

分析问题：

思路1：

        首先，通过两次遍历数组（实际是通过对索引取模来模拟）。在每次遍历中，如果当前元素大于栈顶元素所对应的数组值，就将栈顶元素弹出，并在结果数组中记录当前元素为栈顶元素的下一个更大元素。

        在前 n 个位置时，将索引存入栈中。如果在后续的遍历中找到了更大的元素，就进行相应的处理。

        最终，结果数组 ans 中存储了每个元素对应的下一个更大元素，如果没有则为 -1 。

思路2：

        模拟。根据题目给的要求，我们遍历整个数组，去寻找他下一个更大的值，这里要把数组变成循环数组，因为我们要遍历整个列表。变成循环数组的方法无非就是把遍历的长度加长一点，然后模上len（nums），时间复杂度是O(N**2),但是这个方法用时间换空间，空间复杂度很低。

代码实现：

思路1：

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        n = len(nums)
        stack = []
        ans = [-1]*n 

        for i in range(2*n):
            x = nums[i % n]
            while stack and x > nums[stack[-1]]:
                ans[stack.pop()] = x 
            if i < n:
                stack.append(i)
        return ans

​​

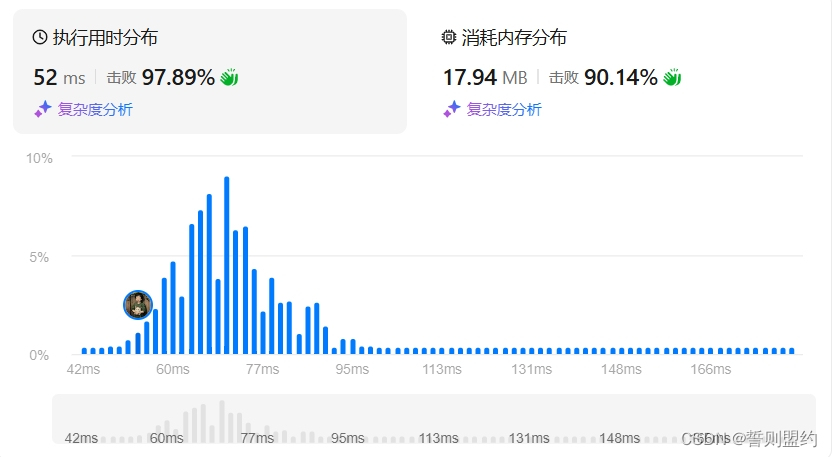
​这种方法时间复杂度和空间复杂度都是比较优越的。 

思路2：

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        n=len(nums)
        ls=[]
        for i in range(len(nums)):
            for j in range(i+1,i+len(nums)+1):
                if j%n==i: 
                    ls.append(-1)
                    break
                elif nums[j%n] > nums[i]:
                    ls.append(nums[j%n])
                    break
        return ls

​​

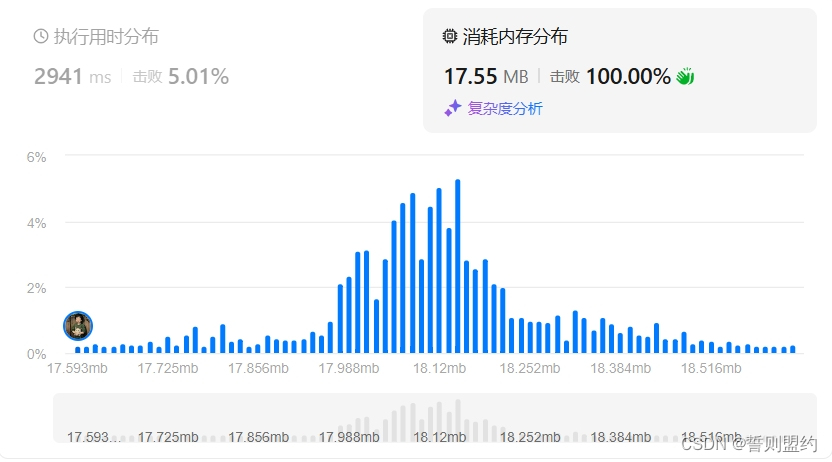
​       思路2是比较容易想出来的一种方法，他的优点就在于空间复杂度较低，通俗易懂。但是时间复杂度较高。

总结：

思路一（使用栈）代码详解：

1. 首先，获取输入数组 nums 的长度 n ，并初始化一个空栈 stack 和结果数组 ans ，其中 ans 中的每个元素初始值都为 -1 。
2. 然后，通过一个循环，模拟对数组进行两轮遍历（实际是通过 i % n 来实现取模操作，达到循环数组的效果）。
3. 对于每次循环获取的当前元素 x ，如果栈不为空且 x 大于栈顶元素对应的数组值，就将栈顶元素弹出，并在结果数组 ans 中记录 x 为弹出元素的下一个更大元素。
4. 在前 n 次循环中（即第一次遍历数组时），将当前索引 i 存入栈中。
5. 最终，返回结果数组 ans ，其中每个位置存储了对应元素的下一个更大元素，如果没有则为 -1 。

思路二（使用两层循环）代码详解：

1. 首先获取输入数组 nums 的长度 n ，并创建一个空列表 ls 用于存储结果。
2. 外层循环遍历数组中的每个元素。对于每个元素，通过内层循环从其右侧的下一个位置开始，模拟循环数组的方式进行查找。
3. 在内层循环中，如果当前位置经过取模后又回到了起始位置（即 j % n == i ），说明在右侧没有找到更大的元素，将 -1 存入结果列表 ls 并结束内层循环。
4. 如果找到了右侧第一个比当前元素大的元素（即 nums[j % n] > nums[i] ），将该更大元素存入结果列表 ls 并结束内层循环。
5. 外层循环结束后，返回结果列表 ls 。

        总的来说，第一段代码通过栈来优化查找过程，空间复杂度相对较低；第二段代码使用两层循环直接查找，逻辑相对简单直观，但时间复杂度可能相对较高。

考点：

• 对数组的遍历操作。
• 循环边界的处理，包括通过取模实现数组的循环遍历。
• 利用栈或多重循环来比较元素大小。

收获：

• 学习了两种不同的方法来解决同一类问题，一种是利用栈的特性，另一种是通过两层循环。
• 加深了对数组操作和循环控制的理解，尤其是在处理循环边界和重复利用数组元素的场景。
• 体会到了不同算法的时间复杂度和空间复杂度的差异，第一段代码使用栈的方式在空间复杂度上相对更优，而第二段代码的两层循环在时间复杂度上可能相对较差。
• 提高了根据问题需求设计合适算法的能力，需要在不同的场景中权衡算法的效率和实现的难易程度。

“我们登上并非我们所选择的舞台，演出并非我们所选择的剧本。”——《Enchiridion》