【数据结构与算法】使用数组实现栈:原理、步骤与应用
【摘要】 栈是一种后进先出(LIFO, Last In First Out)的数据结构。栈是一种只能在一端进行插入和删除操作的线性表。允许进行插入和删除操作的一端称为栈顶(top),另一端称为栈底(bottom)。栈中没有元素时,称为空栈。栈的基本操作包括:push(入栈)、pop(出栈)、peek(查看栈顶元素)和isEmpty(判断栈是否为空)等。
目录
一、引言
🎄栈(Stack)是什么?
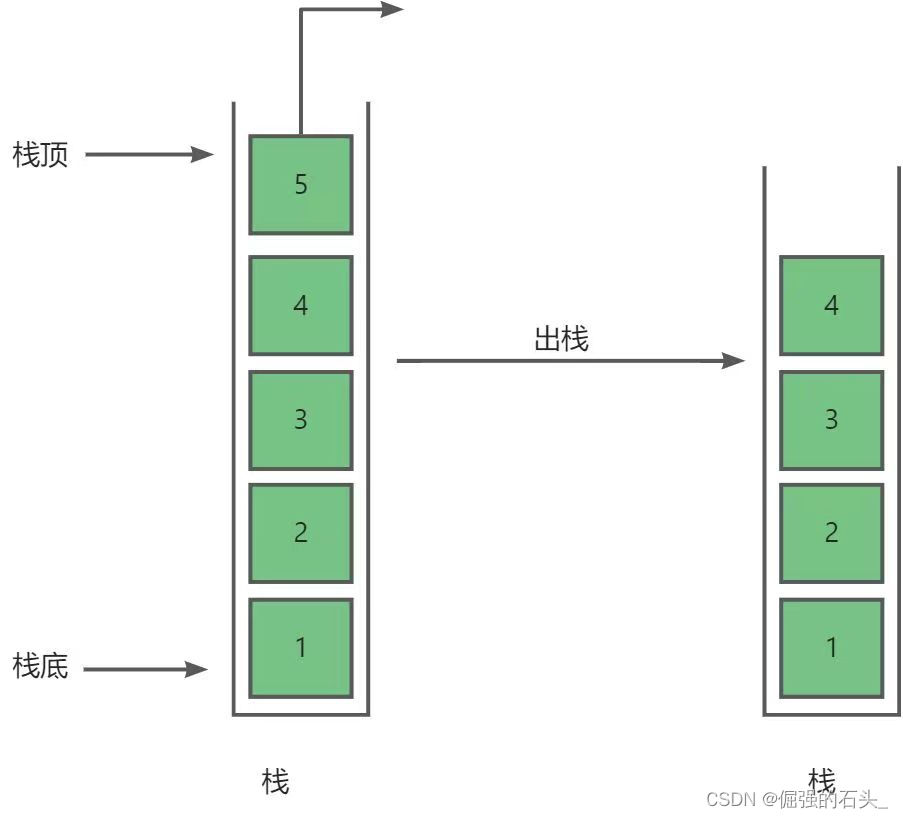
- 栈是一种后进先出(LIFO, Last In First Out)的数据结构。
- 栈是一种只能在一端进行插入和删除操作的线性表。
- 允许进行插入和删除操作的一端称为栈顶(top),另一端称为栈底(bottom)。
- 栈中没有元素时,称为空栈。
- 栈的基本操作包括:push(入栈)、pop(出栈)、peek(查看栈顶元素)和isEmpty(判断栈是否为空)等。
🎄为什么使用数组实现栈?
- 数组是一种线性数据结构,能够连续存储数据,且通过索引可以方便地访问任意位置的元素。
- 因为栈只在栈顶增删,所以基于数组实现,既避免了插入需要移动数据的劣势,又保持了数组访问数据的优势,可以实现高效的栈操作。
二、定义栈结构
🎄栈的结构
- 指向数组的指针(动态开辟的空间)
- 标记栈顶位置的变量 top
- 标记栈的大小的变量 capacity
🎄栈顶位置的指向
需要注意的是:top的指向应该始终保持一致性
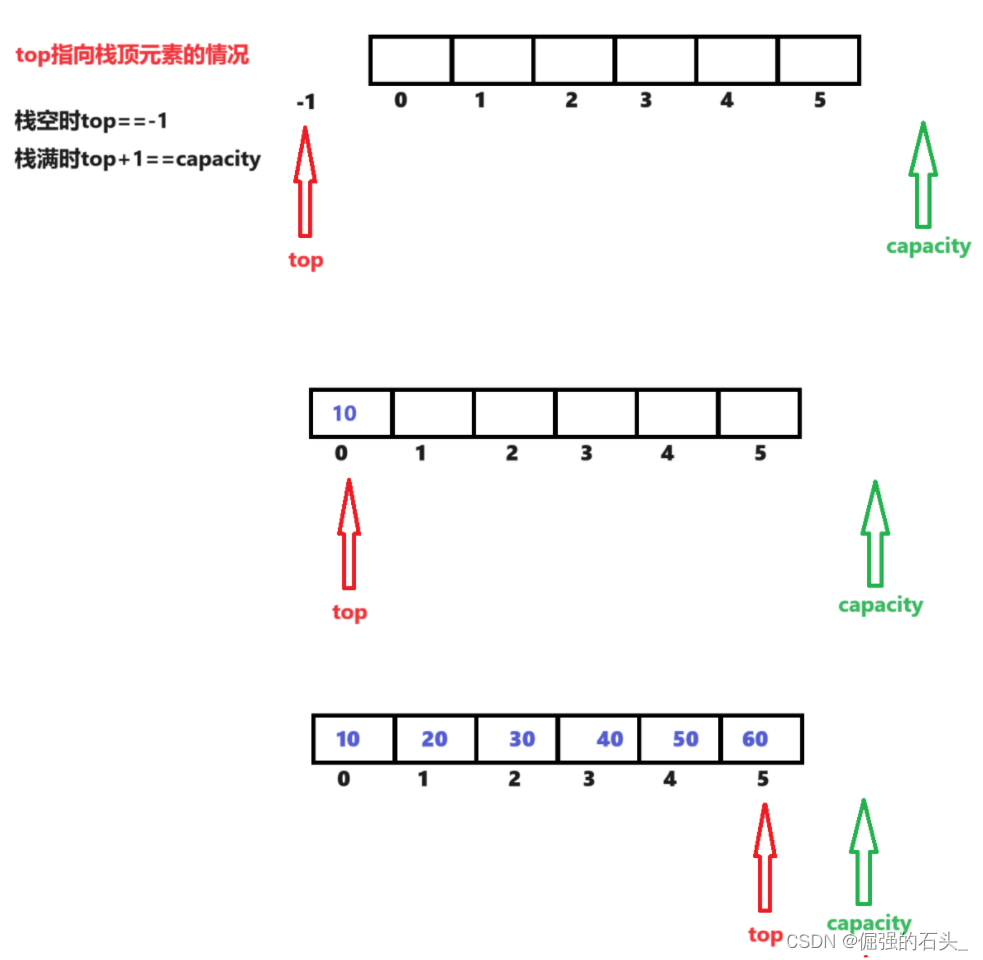
1.如果top指向栈顶元素,初始不能为0,应该指向-1
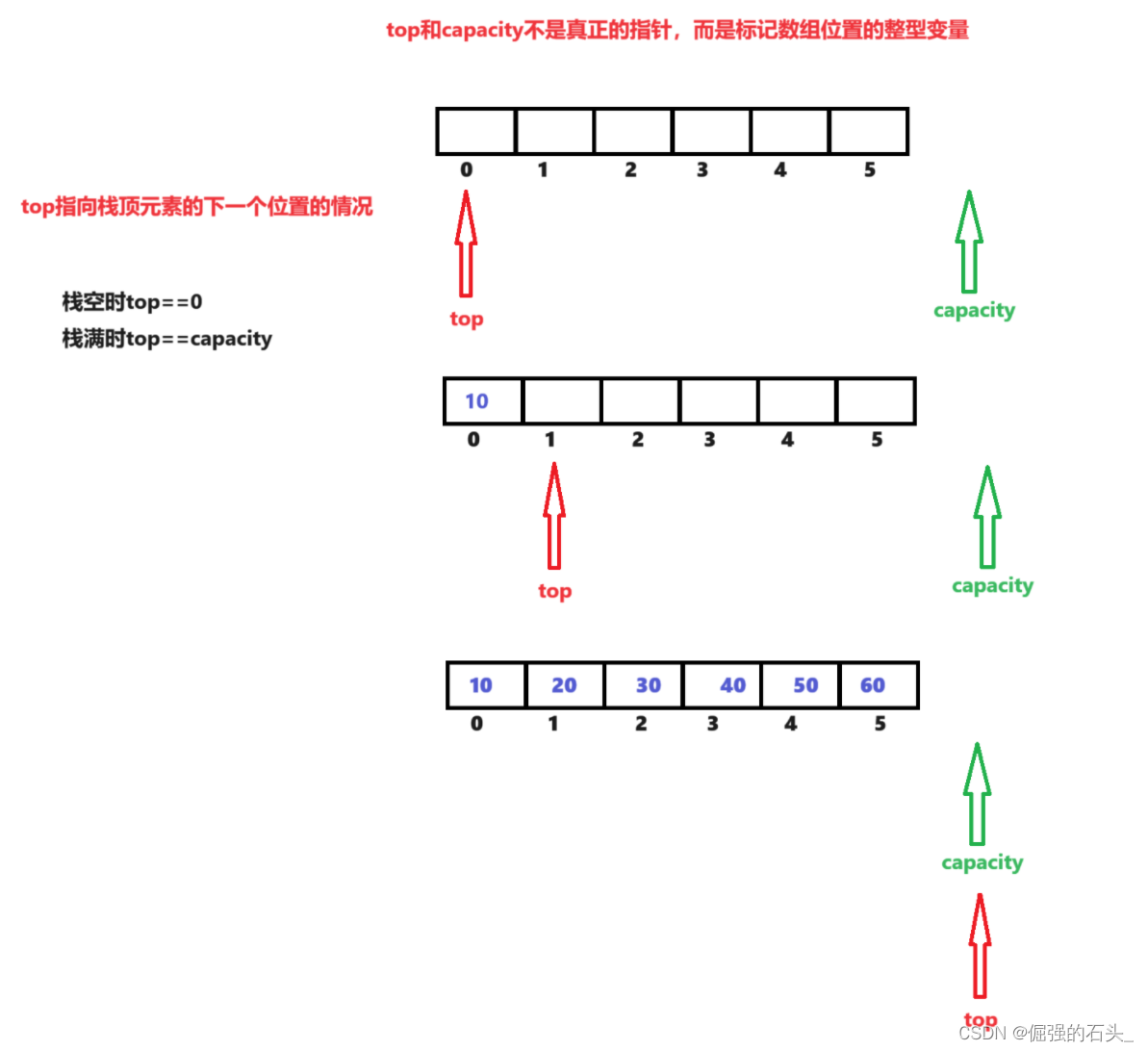
2.如果top初始为0,其应该指向栈顶元素的下一个元素
对应的判定栈满和栈空有所不同
三、实现栈的基本操作
🍃初始化
- 对形参判空
- 数组指针初始指向空
- top和capacity初始化为0(这里top指向的是栈顶元素的下一个位置)
🍃销毁
- 对形参判空
- 释放数组空间
- 数组指针指向空
- top和capacity改为0
🍃入栈
判空
判断是否需要扩容(top和capacity相等)
扩容步骤: 空间二倍增长 ,更新数组指针和容量
数据插入到top位置,top位置++
🍃出栈
- 对形参判空
- 对栈判空
- top--
(该方法对于栈只存在一个元素的情况也可以正确处理)
注意:
即使函数只有一两条语句也还是建议封装成函数,这样可以提高程序的可维护性和可读性
🍃查看栈顶元素
- 对形参判空
- 对栈判空
- 返回top前一个位置的元素
🍃对栈判空
- 对形参判空
- 返回top==0的结果(因为这里top指向的是栈顶元素的下一个元素,所以栈空时top==0)
🍃获取有效数据个数
- 对形参判空
- 返回top (top对应的下标是栈顶的下一个元素,top就是元素的个数)
四、使用数组实现栈的C语言代码
stack.h 栈的头文件
stack.c 栈的实现源文件
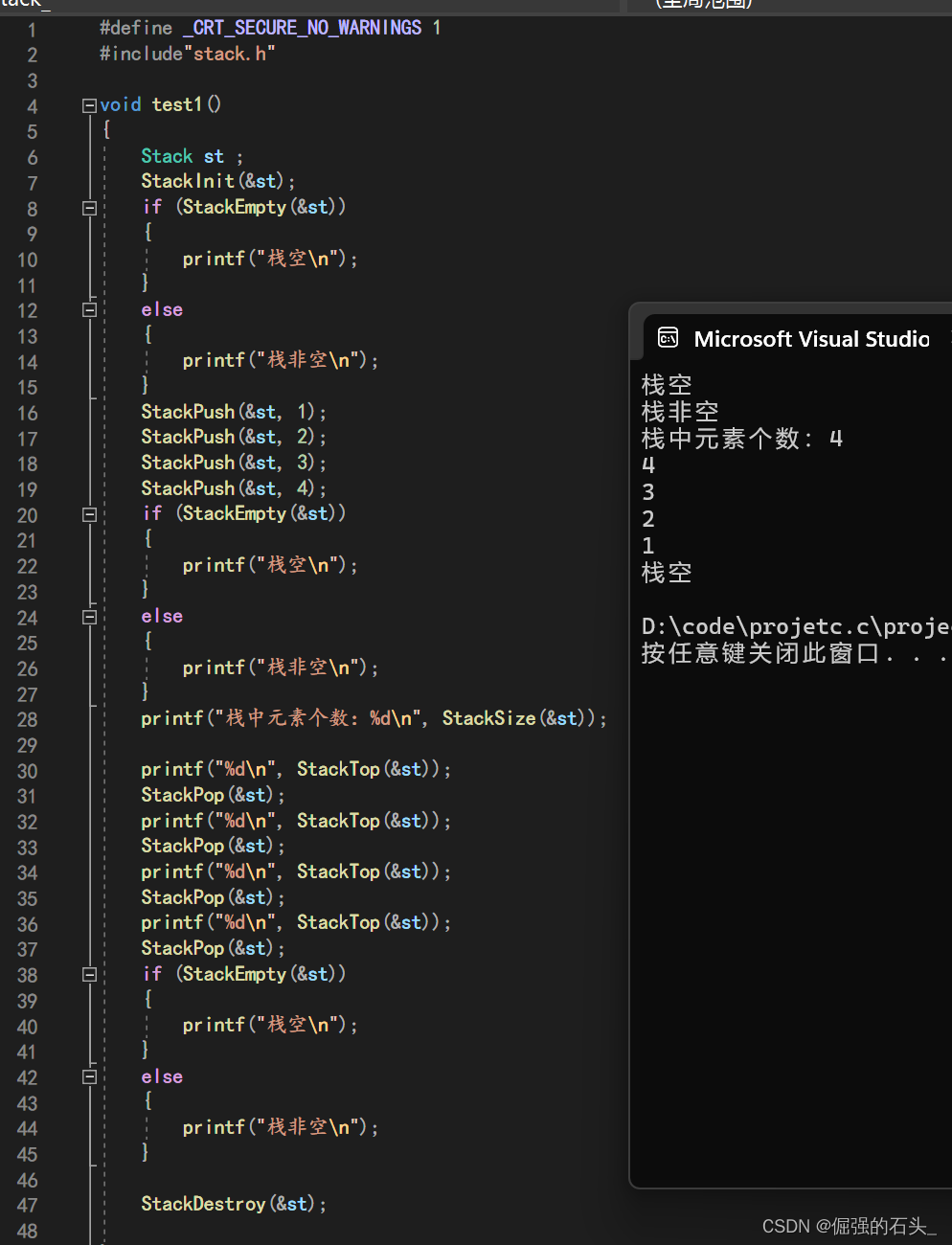
test.c 主函数测试文件
测试结果
五、栈的应用
- 函数调用栈:在程序执行过程中,函数调用是通过栈来实现的。每个函数调用时,其返回地址、局部变量和参数等信息都会被压入栈中,当函数返回时,这些信息会被弹出栈。
- 表达式求值:在编译器中,表达式求值通常使用栈来实现。例如,在解析算术表达式时,可以使用两个栈:一个用于存储操作数,另一个用于存储操作符。
- 浏览器历史记录:浏览器的“前进”和“后退”功能通常使用栈来实现。用户浏览的网页会被压入栈中,当用户点击“后退”按钮时,会从栈中弹出并显示上一个网页。
- 撤销操作:在许多图形编辑器和文本编辑器中,撤销操作通常使用栈来实现。每次编辑操作(如剪切、复制、粘贴等)都会被压入一个撤销栈中,当用户点击“撤销”按钮时,会从栈中弹出并执行相反的操作以撤销上一次编辑。
六、总结
- 使用数组实现栈是一种简单且高效的方法,能够充分利用数组的特性来实现栈的基本操作。
- 在实际应用中,栈具有广泛的应用场景,如函数调用栈、浏览器的前进后退功能以及表达式求值等。
【版权声明】本文为华为云社区用户原创内容,未经允许不得转载,如需转载请自行联系原作者进行授权。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者



评论(0)