前言

什么是有向图

在数学中，一个图(Graph)是表示物件与物件之间的关系的方法，是图论的基本研究对象。一个图看起来是由一些小圆点(称为顶点或结点)和连结这些圆点的直线或曲线(称为边)组成的。

以下数有向图在数学中的定义：

有向图是一个二元组<V,E>，其中

1.V是非空集合，称为顶点集。

2.E是V×V的子集，称为弧集。

而图在数据结构中是中一对多的关系，一般分为有向图和无向图。有向图和无向图最大的区别在于每条路径都带有方向性。在有向图中，边是单向的，每条边连接的两个顶点都是一个有序对。假如把无向图看成是双行道，可以任意穿梭的话，有向图就是一座只有单行道的城市，而且这些单行道是杂乱无章的。因此要求解一处到另一处的路径问题就会变得复杂起来。其实在开发的过程中，我们接触过的很多场景都是有向图，比如：任务调度的依赖关系和社交网络的任务关系等。相对应的概念有：孤立点、简单图、完备图、基本图、强连通图、弱连通图、单向连通图、强连通分支、有向通路。。。等。由于篇幅原因，这里仅仅是抛转引玉点到为止，感兴趣的童鞋，可以自行了解这些相关的概念。

无向图:

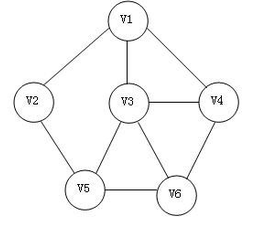
下面就是一个简单的有向图：

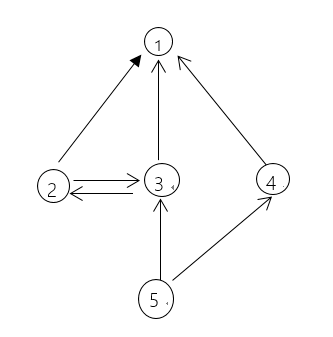
基本概念

有向图的基本概念概括如下：

• 有向图：由一组顶点和一组有方向的边组成，每条有方向的边都连接着一组顶点。

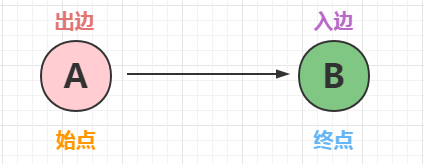
• 顶点的出度：该顶点指出的边的总数。

• 顶点的入度：指向该顶点的边的总数。

• 度：顶点的入度+顶点的出度，称为该顶点的度。自环（起点和终点为同一顶点），此时出度算一度，入度也算一度。

• 有向路径：由一系列顶点组成，其中每个顶点都存在一条有向边，由它指向序列中的下一个顶点

• 有向环：至少含有一条边，且起点和终点相同的有向路径。虽然有向图中环的数量和大小也是有用的信息，但是在实际应用过程中，我们更多的只关心是否存在有向环。

• 简单有向环：除了起点和终点外，不含有重复的顶点和边的环。

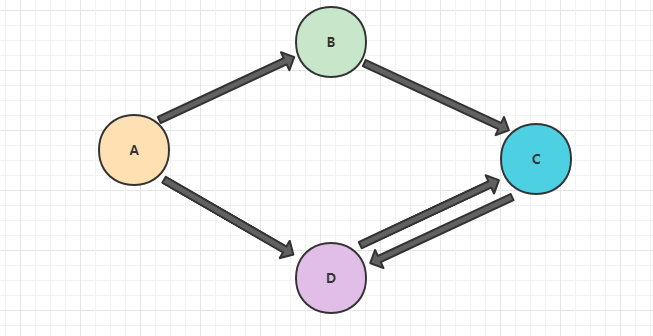
代码实现

实现流程

1. 自定义有向图，并用邻接表进行储存。实现所有途径和最短路径的求解，通过isinstance() 函数判断数据类型.

2. 对输入的数据进行存储

如何实现有向图

使用关键字class,创建DirectedGraph类,并且定义__init__()方法,初始化变量，存储输入的数据。代码如下:

class DirectedGraph(object):
     def __init__(self,d):
         if isinstance(d,dict):
             self.__graph = d
         else:
             self.__graph = dict() #字典
             print('发生错误')

在DirectedGraph类中定义生成路径的__generatePath()方法.代码如下:

     def __generatePath(self,graph,path,end,results):
         curret = path[-1]
         if curret == end:
             results.append(path)
         else:
             for n in graph[curret]:
                 if n not in path:
                     self.__generatePath(graph,path+[n],end,results)

在DirectedGraph类中定义searchPath()方法，搜寻并展示所有路径:

     def searchPath(self,start,end):
         self.__results = []
         self.__generatePath(self.__graph,[start],end,self.__results)
         self.__results.sort(key=lambda  x:len(x))                    #按路径长度进行排序
         print(self.__results[0][0],'到',self.__results[0][-1],'的路径是:')
         for path in self.__results:
             print(path)

终于到了见证奇迹的时刻，验证代码是否正确：

#输入一个字典
d={'A':['B','C','D'],
     'B':['E'],
     'C':['D','F'],
     'D':['B','E','G'],
     'E':['D'],
     'F':['D','G'],
     'G':['E']}

g=DirectedGraph(d)
#遍历不同顶点的所有路径
g.searchPath('A','D')
g.searchPath('A','G')
g.searchPath('A','F')

执行结果如下：