0.简介

作为常用的滤波器形式，低通滤波是一种适中的滤波处理方式，相较于卡尔曼滤波算法和滑动平均滤波而言。其计算量适中，同时能拿到一个较为合适的结果。低通滤波算法可以解决这种长期可靠，短期噪声大的传感器，并有效地实现噪声的滤除。

1. 相关代码

oldData表示上一次的输出Y(n-1), newData表示新的输入X(n)； deltaT 采样周期, Fcut 截止频率 。

   float LopPassFilter_RC_1st(float oldData, float newData, float a)
　　{
　　　　return oldData * (1 - a) + newData * a;
　　}

　　//计算比例系数a:

　　float LopPassFilter_RC_1st_Factor_Cal(float deltaT, float Fcut)
　　{
　　　　return deltaT / (deltaT + 1 / (2 * M_PI * Fcut));
　　}

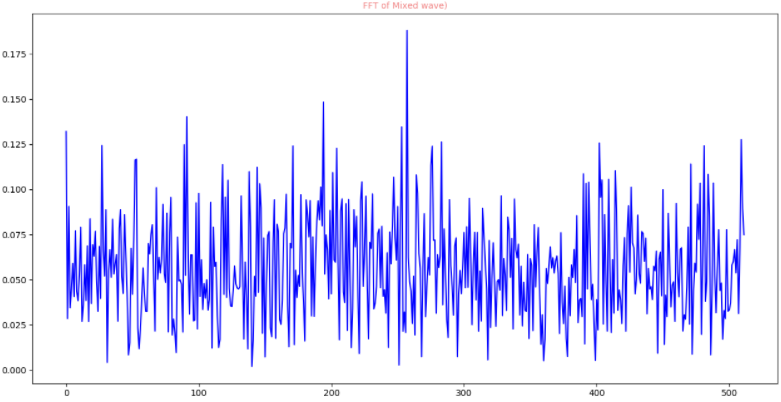
FFT源频谱

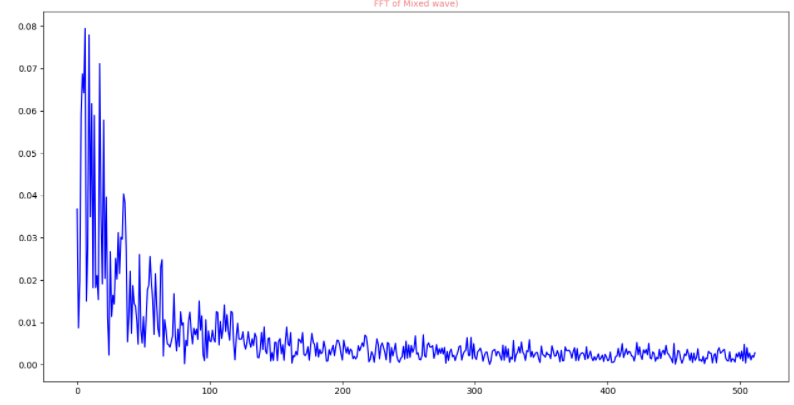
一阶滤波优化后

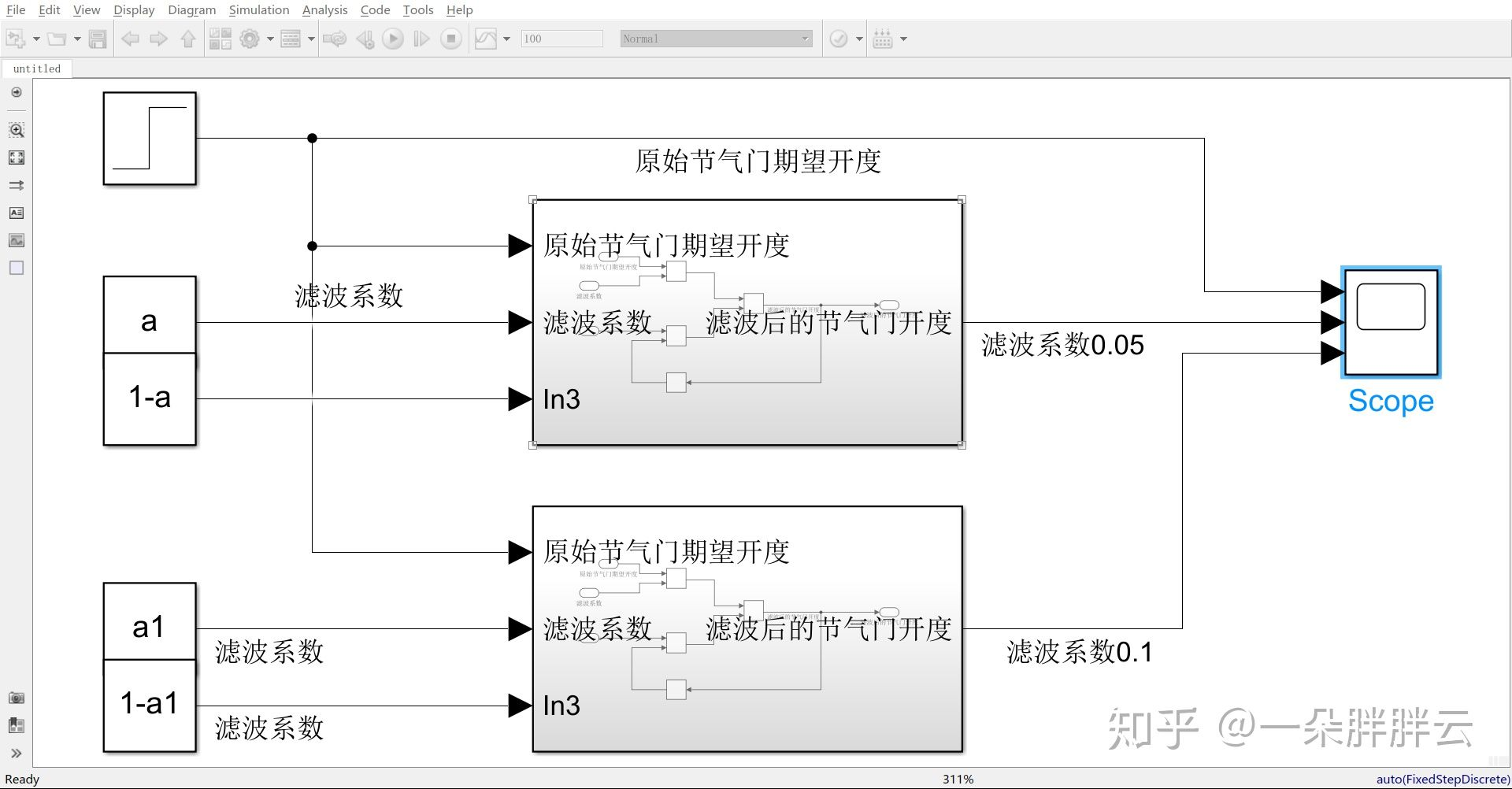
2. 一阶滤波算法的特性

这里引用了一朵胖胖云写的相关博客内容。介绍了以节气门控制为例，用simulink进行建模仿真的低通滤波器：

假定期望节气门开度变化：0-30%，调整滤波系数分别为0.05和0.1，低通滤波后得到如下曲线：

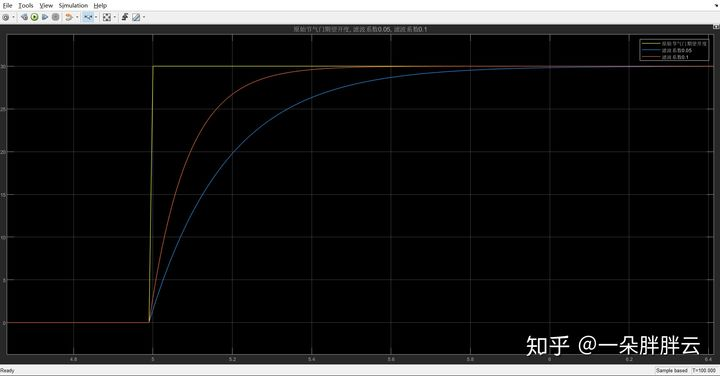
由图可知：

1）滤波系数越大，则更快达到目标开度，但曲线平滑性较差

2）同样的滤波系数越小，则更慢达到目标开度，但曲线更加平滑，且稳定

，因此在实际标定过程中，我们需要根据实际情况，平衡灵敏度和稳定性，来确定最终的滤波系数。

…详情请参照古月居

<!-- # 3. 一阶滤波算法的不足 1. 关于灵敏度和平稳度的矛盾 > 滤波系数越小，滤波结果越平稳，但是灵敏度越低； > 滤波系数越大，灵敏度越高，但是滤波结果越不稳定。 2. 一阶滤波无法完美地兼顾灵敏度和平稳度。有时，我们只能寻找一个平衡，在可接受的灵敏度范围内取得尽可能好的平稳度。而在一些场合，我们希望拥有这样一种接近理想状态的滤波算法。即： > 当数据快速变化时，滤波结果能及时跟进（灵敏度优先）； > 当数据趋于稳定，在一个固定的点上下振荡时，滤波结果能趋于平稳（平稳度优先）。 3. 关于小数舍弃带来的误差 这部分要求我们需要提供较高的浮点精度来给到一阶滤波算法。如果无法使用较高的浮点运算，那则建议使用**滑动平均滤波**，在低频段较之卡尔曼滤波和低通滤波，其频谱得到的幅值是其余二者的数十倍，这是由于求均值时，将部分噪声数据也计算到信号数据中导致的，因此可以看出，滑动平均滤波不能有效得将噪声数据滤掉，不过在工程因为计算简单**，浮点运算少，甚至没有**，所以得到广泛运用。 # 4. 一阶高通滤波代码 在讲完一阶低通后，作者也打算补充一下一阶高通滤波器，来作为文章的结尾。 一阶高通滤波器含义和一阶低通滤波器含义刚好相反，可以通过高于设定频率的波形。 oldData表示上一次的输出Y(n-1) , oldDataInput表示上一次的输入X(n-1), newData表示新的输入X(n)； deltaT 采样周期, Fcut 截止频率 。 ```cpp float LopPassFilter_RC_1st(float oldData, float oldDataInput, float a) 　　{ 　　　　return a * (oldData + float newData - oldDataInput); 　　} 　　//计算比例系数a: 　　float LopPassFilter_RC_1st_Factor_Cal(float deltaT, float Fcut) 　　{ 　　　　return 1 / 1 + (2 * M_PI * Fcut * deltaT)); 　　} ``` # 5. 参考链接 [https://blog.csdn.net/moge19/article/details/87389728](https://blog.csdn.net/moge19/article/details/87389728) [https://blog.csdn.net/sinat_23338865/article/details/52672721](https://blog.csdn.net/sinat_23338865/article/details/52672721) [https://www.cnblogs.com/Lxk0825/p/9908915.html](https://www.cnblogs.com/Lxk0825/p/9908915.html) [https://zhuanlan.zhihu.com/p/115560016](https://zhuanlan.zhihu.com/p/115560016) [https://zhuanlan.zhihu.com/p/108101458](https://zhuanlan.zhihu.com/p/108101458)