【多式联运】基于帝国企鹅算法+遗传算法+粒子群算法求解不确定多式联运路径优化问题【含Matlab源码 2073期】

一、联运运输简介

1 引言
运输问题(Transportation Problem)是一类特殊的线性规划问题,最早是由Hichcock于1941年提出的,由于它不仅能解决物资的合理调运和车辆的合理调度,而且许多实际问题如生产存储问题、工厂选址问题等经过适当变换后可转化为运输问题进行求解,一些理论问题如最小费用流问题也与它息息相关,因此研究运输问题具有相当重要的实际意义。

多式联运(Multimode Transportation)是现代物流系统中竞争协作的最佳方式,研究多式联运的运输方式选择,对于实现运输费用或时间的节约,提高交通运输服务水平以及社会效益具有重要的意义。建立了多城市间选择最优运输方式组合的模型并给出了基于Dijkstra的启发式算法;建立了基于多维权有向图的多式联运运输方式选择模型。

2 多式联运运输问题的数学模型
设有一个多式联运运输问题:某种物资有m个产地,n个销地,从每个产地至每个销地都要经过l段运输区间,任意一段运输区间有g种运输方式可以选择,各运输方式所需的费用c不同,当从一种运输方式转换到另一种运输方式时,需要一定的中转费用d,问如何选择从不同产地到不同销地的运输量以及各自的运输方式使得既满足产销地的供需约束,又使得所需的总费用最少。

模型记号:
ai:各产地的产量,i=1,2,…,m;
bj:各销地的销量,j=1,2,…,n;
cpijk:从产地i运往销地j的物资在第k段运输区间选择第p种运输方式所需的单位运费,p=1,2,…,g,k=1,2,…,l;
dpqijk:从产地i运往销地j的物资在第k段运输区间开始时从第p种运输方式转换至第q种运输方式所需的中转需用,p,q=1,2,…,g,k=2,3,…,l;
xij:从产地i运往销地j的物资运输量;
yijk:从产地i运往销地j的物资在第k运输区间选择的运输方式,取值为1至g的整数;

上述多式联运运输问题的数学模型如下:

若是从某个产地i到销地j的分段运输区间小于l段,则可令对应的运输区间选择任何一种运输方式所需的单位费用以及中转费用均为0后扩展为l段;同样若从产地i运往销地j的物资在第k段运输区间的运输方式小于g种,则可令对应的运输方式所需的中转费用为充分大的正数从而扩展为g种。由于不平衡运输问题可以通过设立虚拟产地或是虚拟销地转化

为平衡运输问题,从而下面增加一个平衡假设,即:

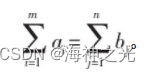
3 求解多式联运运输问题的混合遗传算法
由前面的分析可以看出,多式联运运输问题是一个组合优化问题其中包括运输量的分配以及运输方式的选择两个方面。用遗传算法来进行求解,由于运输问题本身是一个约束优化问题,对于约束的处理一般有两种方法,一种是采用罚函数的方法将解从不可行区域引导至可行区域;另一种是设计可行解的生成方法及保持可行性的遗传算子,使得解始终在可行区域中寻优。采用第二种方法,通过设计满足可行性的混合编码以及两种保持可行性混合遗传算子来实现遗传算法的寻优。

3.1 染色体混合编码
采用两种方式的混合编码,首先对于运输量,采用最自然的矩阵编码方式,即用矩阵[xij]mn表示一个运输方案,其中xij表示从产地i到销地j的运输量;其次对于从产地i到销地j的多式联运运输方式采用长度为l的自然数编码,每个位置的取值为1到g的整数,表示对应运输区间的运输方式。如

3.2 适应度函数定义
令yijk表示向量yij的第k个分量,其值即表示某种运输方式,则给定一组解([xij]mn,[yij]mn),其适应度函数为式(1)所示。

3.3 初始可行解的生成方法
由于多式联运运输问题是一个约束优化问题,故如何生成初始可行解相当重要。针对前述混合编码方式,设计如下的初始解生成方法:

{repeat
从集合T={1,2,…,mn}中随机取一个整数T®;
将T®转化为相应的行列:i=[(T®-1)/n+1],这里[]表示函数取整;j=(T®-1)mod n+1;
令xij=min{ai,bj};令yij为分量取值在{1,2,…,g}之间长度为l的随机向量;
更新ai:=ai-xij;bj:=bj-xij;T:=T\T®;
Until T=Ø}

3.4 算法流程
步骤1 产生一个初始种群,种群规模为N,计算出种群中个体的适应值,适应度函数即问题式(1)的目标函数值,令t:=1。
步骤2 在父代种群中以轮盘赌方式选择个体形成杂交种群池C(t),设其规模为M。
步骤3 随机选择C(t)中的个体P1和P2进行杂交算子操作以生成新个体C1和C2。
步骤4 重复步骤3直到产生2M个新个体形成杂交子种群。
步骤5 从父代种群及杂交子种群以pm的概率选取个体用变异算子进行变异。
步骤6 从父代种群、杂交子种群以及变异子种群中计算各个体的适应值,取其中适应值最小的N个个体形成子代种群,令t:=t+1。
步骤7 判断终止条件是否满足,如果满足则输出当前种群的最优个体作为问题的最优解,否则转步骤2继续迭代。

4 碳政策介绍
碳排放是指每个人、家庭或每家公司日常释放的温室气体数量，以二氧化碳的影响为单位，用以衡量人类活动对生态环境的影响。强制碳排放政策是一种基于政府规定的碳排放上限的碳政策，在此政策下企 业不会产生额外的碳排放成本。碳税是针对二氧化碳排放所征收的税费，即以政府规定的每单位碳排放税率与企业碳排放量的乘积作为所需要缴纳的碳排放费用，并将其计入成本中构成系统总成本。截至2019 年，已有芬兰、澳大利亚、英国、瑞典、加拿大和日本等国开征碳税，尽管当前我国并未实施，但发改委早在“2016 中国碳交易市场发展论坛”明确表示碳税在我国的必要性和可行性，并正在与财政部等部门积极准备启动碳税的前期工作。碳交易是指政府根据各地温室气体排放量、控排企业纳入情况等，核定一定时期内的碳排放总额，单位配额即每吨二氧化碳当量排放权，当初始配额不足或多余时企业按自身需要进行买卖，属于数量干预的减排措施，其本质是科斯理论中提到的产权。在我国现行的碳交易政策下，交易价格作为一种市场机制，具有动态性和随机性，时空差异性尤为显著。碳交易的核心是排放额度，企业不仅可以通过支付相应的资金进行购买来获得额外排放额度补贴，也可以通过出售多余的碳排放额度来获取一定的资金，产生相应的碳排放成本或收益。

二、部分源代码

clc;
clear all;
close all;
warning off
%%
noRng=1;
rng(‘default’)
rng(noRng)
%%
global data
data.numN=15; %节点数量
data.Cap_Ts=xlsread(“节点处的最大中转运输能力.xlsx”);
temp=round(rand(data.numN,3)10+15)10;
data.Cap_Ts(:,2:end)=temp;
data.Windows=xlsread(“节点的时间窗.xlsx”);
data.D=xlsread(“节点间距离.xlsx”);
data.Cap_Tp=xlsread(“节点间最大运输能力.xlsx”);
data.T=data.D;
data.v=[76,60,30];
for i=1:length(data.Cap_Tp(:,1))
no1=data.Cap_Tp(i,1);
no2=data.Cap_Tp(i,2);
for j=1:3
if isnan(data.Cap_Tp(i,2+j))
data.D(i,2+j)=nan;
end
end
data.T(i,[3,6,9])=round(data.D(i,3:5)./data.v/1.2);
data.T(i,[4,7,10])=round(data.D(i,3:5)./data.v);
data.T(i,[5,8,11])=round(data.D(i,3:5)./data.v/0.8);
end
data.Windows(:,3)=data.Windows(:,3).(1-rand(size(data.Windows(:,3))));
data.Windows(:,4)=data.Windows(:,4).(1+rand(size(data.Windows(:,3))))+10;
data.Windows(:,3:4)=max(0,round(data.Windows(:,3:4)+randn(size(data.Windows(:,3:4)))));
data.Windows(:,5)=max(data.Windows(:,4));
data.CT=[0,3.09,5.23; % 转换成本
3.09,0,26.62;
5.23,26.62,0];
data.TT=[0,1,1; %转换时间
1,0,2;
1,2,0];
data.ET=[0,1.56,6; % 转换碳排放
1.56,0,3.12;
6,3.12,0];
data.q=[120,150,180];

data.E0=[0.796,0.028,0.04];
data.CW=[30,50];
data.S=1;
data.E=15;
data.alpha=0.8;
data.beta1=0.8;
data.beta2=0.8;
data.beta3=0.8;
data.C0=[0.3,0.2,0.1]; %三种运输方式的运输成本
data.weight=[1,1];
data.maxB=100000;
data.maxE=21000;
%%
%%
data.numQ=100;
for i=1:data.numQ
if rand<0.5
data.q0(i)=rand*(data.q(2)-data.q(1))+data.q(1);
else
data.q0(i)=rand*(data.q(3)-data.q(2))+data.q(2);
end
end
%%
G=graph(data.D(:,1),data.D(:,2),data.D(:,1)*0+1);
figure
plot(G)
set(gca,‘LooseInset’,get(gca,‘TightInset’))
%%
lb=0;
ub=1;
dim=length(data.D(:,1))*3;
option.lb=lb;
option.ub=ub;
option.dim=dim;
if length(option.lb)==1
option.lb=ones(1,option.dim)*option.lb;
option.ub=ones(1,option.dim)*option.ub;
end
option.fobj=@aimFcn_1;
option.showIter=0;

%% 算法参数设置 Parameters
% 基本参数
option.numAgent=20; %种群个体数 size of population
option.maxIteration=100; %最大迭代次数 maximum number of interation
%% 遗传算法
option.p1_GA=0.7;
option.p2_GA=0.1;
%% 粒子群
option.w_pso=0.1;
option.c1_pso=1.2;
option.c2_pso=1.2;
%% AFO

option.v_lb=-(option.ub-option.lb)/4;
option.v_ub=(option.ub-option.lb)/4;
option.w2=0.5; %weight of Moving strategy III
option.w4=1;%weight of Moving strategy III
option.w5=1;%weight of Moving strategy III
option.pe=0.01; % rate to judge Premature convergence
option.gap0=ceil(sqrt(option.maxIteration2))+1;
option.gapMin=5; % min gap
option.dec=2; % dec of gap
option.L=10; % Catastrophe
%% DE
option.F=0.5;
option.CR=0.5;
%%
str_legend=[{‘GA’},{‘PSO’},{‘AFO’}];
aimFcn=[{@GA},{@PSO},{@AFO3}];
%% 初始化
rng(noRng)
x=ones(option.numAgent,option.dim);
y=ones(option.numAgent,1);
for i=1:option.numAgent
x(i,:)=rand(size(option.lb)).(option.ub-option.lb)+option.lb;
y(i)=option.fobj(x(i,:),option,data);
end

三、运行结果

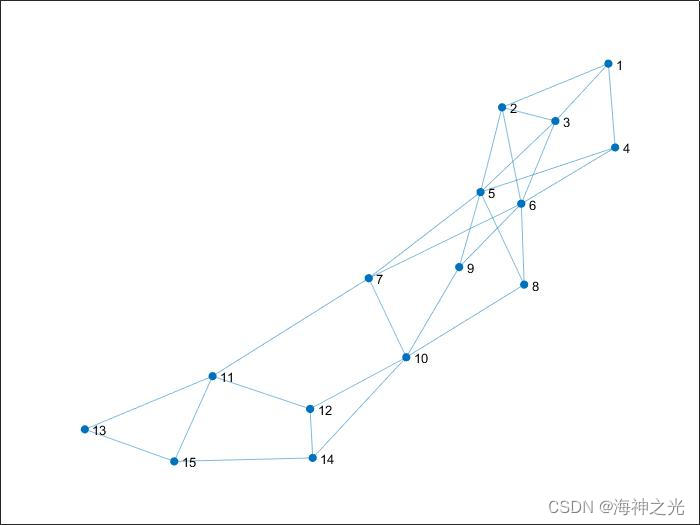
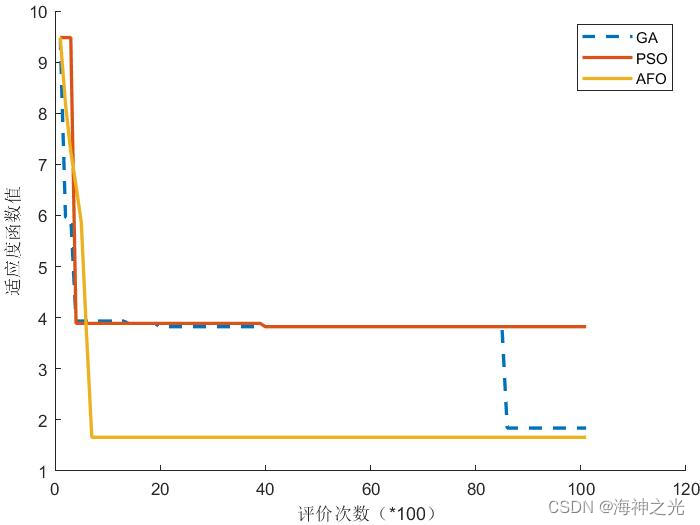
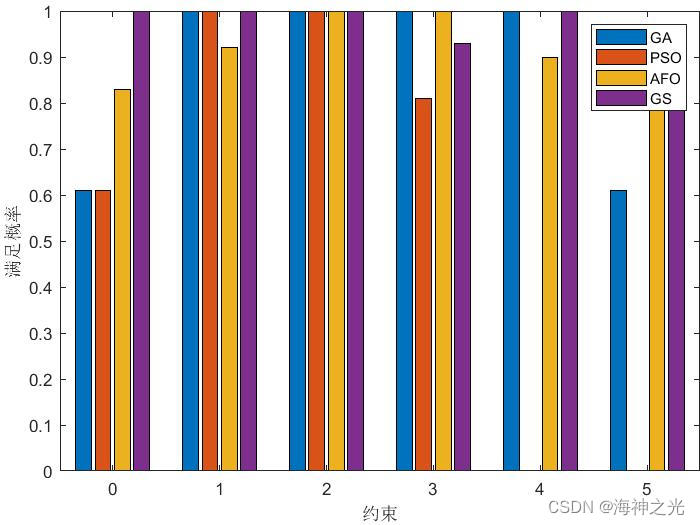
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]俞武扬.多式联运运输问题的混合遗传算法[J].计算机工程与应用. 2009,45(33)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/126671456