🤵‍♂️ 个人主页: @计算机魔术师
👨‍💻 作者简介：CSDN内容合伙人，全栈领域优质创作者。

🌐 推荐一款找工作神器网站: 牛客网🎉🎉|笔试题库|面试经验|实习招聘内推
还没账户的小伙伴 速速点击链接跳转牛客网登录注册 开始刷爆题库，速速通关面试吧🙋‍♂️

该文章收录专栏
✨— 机器学习 —✨

@toc

@[toc](【机器学习】向量化计算 —机器学习路上必经路)

一、求解矩阵

在求解矩阵中，往往有很多很好的，经过高度优化的线性代数库，如octave，matlib，python numpy, c++,java.
我们使用这些线性代数库，可以短短几行实现 所要的效果。

阅读本文内容（需要一点点线性代数的知识）

二、例一

例如 求公式：

$h(x) = \sum_{i=1}^n\theta_i*x_i$
我们可以通过循环每一个值来求 每一个 $i$所对应的结果，但此时循环的时间复杂度为 $O(n)$ ， 我们可以把 $\theta_i(i=1,2,3...n)$ 看为 $n$维的列向量， $x_i$作为 $n$维的列向量，则原公式即为求两个向量的内积 $\theta^T*x_i$ 来求得方程，这样在numpy中仅仅需要一行代码。如下图（演示代码为octave(matlib开源版））

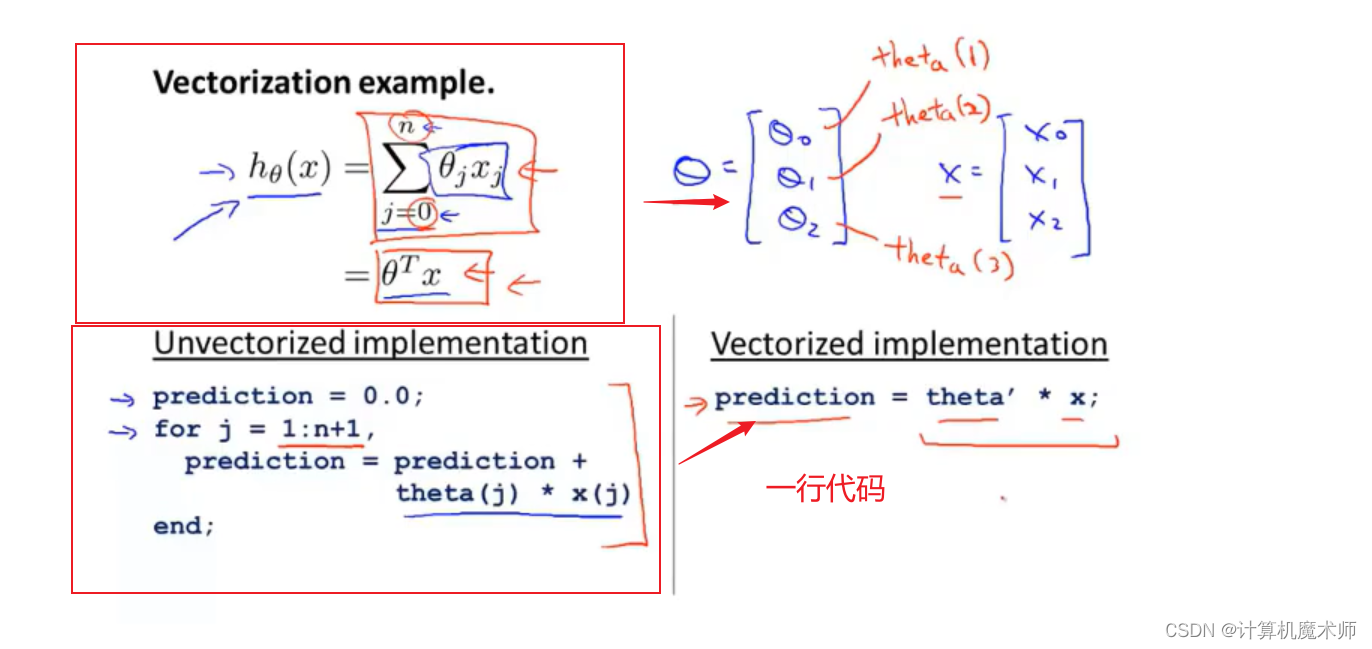
c++实现

三、例二

• 再看一个复杂一点的例子：

（对梯度下降还不了解建议先食用文章：机器学习】浅谈正规方程法&梯度下降）
在梯度下降(Gradient descent)同步更新参数 $\theta_i(i=1,2,3...m)中$

我们可以通过循环 $i$得到每个参数更新，但我们是否能用例子一的方法 简化呢，

如图:

我们将所求式子变为 向量之间的运行，
$\theta = \theta - \alpha * δ$
(其中： $δ$ = $\sum_{x=1}^n \frac{（h_\theta(x) - y_i）^2}{ n }*x_i$, $h_\theta(x) - y_i$ 是一个实数， $x_i$是特征维度的列向量)

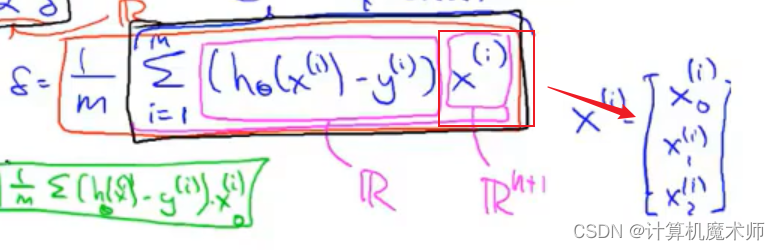
此时参数 $\theta_i$也能同步更新，符合要求

四、写在最后

在面对，数据为百万级别，千万级别，或者特征为百万级别，特征级别，向量化计算对提高运算效率非常高效，比for循环要好用得多，这在机器学习中是非常常见的，一定要掌握