【VMD优化】基于matlab遗传算法优化VMD参数【含Matlab 1980期】
一、获取代码方式
获取代码方式1:
完整代码已上传我的资源:【VMD优化】基于matlab遗传算法优化VMD参数【含Matlab 1980期】
点击上面蓝色字体,直接付费下载,即可。
获取代码方式2:
付费专栏优化求解(Matlab)
备注:
点击上面蓝色字体付费专栏优化求解(Matlab),扫描上面二维码,付费299.9元订阅海神之光博客付费专栏,凭支付凭证,私信博主,可免费获得5份本博客上传CSDN资源代码(有效期为订阅日起,三天内有效);
点击CSDN资源下载链接:5份本博客上传CSDN资源代码
二、遗传算法优化VMD参数简介
1 变分模态分解
VMD分解算法实际上是一个变分问题的求解过程, 它是将原信号分解为K个模态函数uk (t) , 使得每个模态函数的估计带宽之和最小, 则相应的约束变分模型可表达为
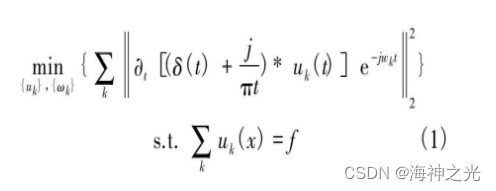
式中:{uk}={u1, …, uk}表示的是分解得到的K个子模态;{wk}={w1, …, wk}表示的是各分量的频率中心。
为了将上述约束性变分问题转变为非约束性变分问题, 引入二次惩罚项因子α和拉格朗日乘子λ (t) , 则扩展的拉格朗日表达式为
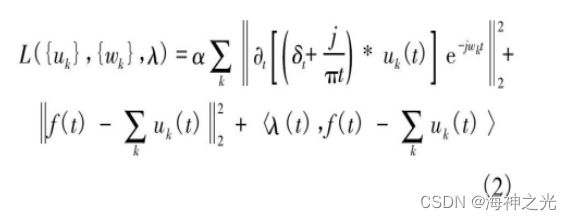
式中:α为惩罚参数;λ为拉格朗日乘子。采用乘法算子交替方向法 (Alternate direction method of multipliers, ADMM) [10]解决变分问题, 通过迭代更新ukn+1、wkn+1以及λn+1得到上述函数的最优解。
ukn+1的取值问题可表达为

利用Parseval傅立叶等距变换, 上式可变为

2) 根据式 (4) 、式 (5) 在频域内更新uk、wk;
- 更新λ, 其中

2 遗传算法VMD参数优化
利用VMD算法进行信号分解时需要设置参数, 研究发现在进行分解时, 模态数K和惩罚参数α对分解的结果影响较大。实际获取的信号是复杂多变的, 模态数K和惩罚参数α难以确定, 因此选择合适的参数组合是利用VMD算法进行信号分解的关键。
如果设置一个参数不变, 优化另一个参数, 通过这种方式讨论对去噪效果的影响, 就忽略了两个参数相互作用的结果, 陷入局部优化的僵局。遗传算法 (GA) 是一种智能优化算法, 具有较强的全局非线性优化能力[12], 因此引入遗传算法, 借助于适应度函数对目标函数在解空间进行全局并行随机搜索, 快速准确地获取优化参数。
利用遗传算法求解优化问题时, 主要需要经过6个步骤, 编码、初始群体生成、适应度值评价检测、选择、交叉、变异, 使得种群进化为新一代更好适应性的种群。图1是建立适应度函数的优化结果。
三、部分源代码
%% 基于遗传算法(Genetic Algorithm,GA)优化变分模态分解(variational mode decomposition,VMD)参数
clc
clear all
close all
% 读取数据
data=load('齿轮折断状态测试组).txt');
%采样频率
fs=12800;
% 信号长度
len=1000;
s=data(1:len);
% 采样时间
t = (0:len-1)/fs;
%% 设定遗传算法参数
maxgen=10; % 进化代数,即迭代次数
sizepop=10; % 种群规模
pcross=0.8; % 交叉概率选择(Pc:0-1)
pmutation=0.1; % 变异概率选择(Pm:0-1)
nvar=2; % 优化参数个数为2,分别为VMD的alpha和K
lenchrom=ones(1,nvar); % 个体长度
% 参数范围(VMD的alpha和K)
bound=[500 2000;
3 10];
% 种群初始化
individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]); %将种群信息定义为一个结构体
avgfitness=[]; %存储每一代种群的平均适应度
bestfitness=[]; %存储每一代种群的最佳适应度
bestchrom=[]; % 存储适应度最好的染色体
%初始化种群
for i=1:sizepop
%随机产生一个种群
individuals.chrom(i,:)=Code(lenchrom,bound); %编码(binary和grey的编码结果为一个实数,float的编码结果为一个实数向量)
x=individuals.chrom(i,:);
%计算适应度
individuals.fitness(i)=objfun(x,s);
end
%找最好的染色体
[bestfitness bestindex]=min(individuals.fitness); %[m n]=min(b) m最小值 n列号
bestchrom=individuals.chrom(bestindex,:); %最好的染色体
avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度
% 记录每一代进化中最好的适应度和平均适应度
trace=[avgfitness bestfitness];
%% 迭代寻优
start_time_train=cputime;
for i=2:maxgen
disp(['迭代次数:',num2str(i)])
% 选择
individuals=Select(individuals,sizepop); %选择后的新种群
avgfitness=sum(individuals.fitness)/sizepop;
% 交叉
individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);
% 变异
individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,i,maxgen,bound);
% 计算适应度
for j=1:sizepop
x=individuals.chrom(j,:); %解码
individuals.fitness(j)=objfun(x,s);
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
四、运行结果



五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 刘嘉敏,彭玲,刘军委,袁佳成.遗传算法VMD参数优化与小波阈值轴承振动信号去噪分析[J].机械科学与技术. 2017,36(11)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
文章来源: qq912100926.blog.csdn.net,作者:海神之光,版权归原作者所有,如需转载,请联系作者。
原文链接:qq912100926.blog.csdn.net/article/details/125770194
- 点赞
- 收藏
- 关注作者

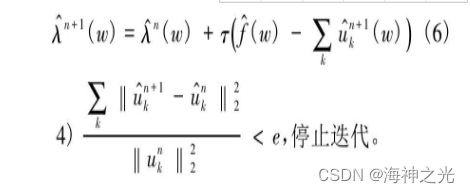

评论(0)