【数学建模】基于matlab三维数据可视化（华为杯）【含Matlab源码 139期】

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【数学建模】基于matlab三维数据可视化（华为杯）【含Matlab源码 139期】

获取代码方式2：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、案例背景

在数学建模过程中我们经常遇到可视化三维数据的情况。以2017年研究生数学建模比赛A题（无人机在抢险救灾中的优化运用）为例，这个问题的背景是：
2017年8月8日，四川阿坝州九寨沟县发生7.0级地震，造成了不可挽回的人员伤亡和重大的财产损失。由于预测地震比较困难，及时高效的灾后救援是减少地震损失的重要措施。无人机作为一种新型运载工具，能够在救援行动中发挥重要作用。为提高其使用效率，请你们解决无人机优化运用的几个问题。
附件1给出了震区的高程数据，共有2913列，2775行。第一行第一列表示(0,0)点处的海拔高度值(单位：米)，相邻单元格之间的距离为38.2米，即第m行第n列单元格中的数据代表坐标(38.2(m-1), 38.2(n-1))处的高度值。
除另有说明外，本题中的无人机都假设平均飞行速度60千米/小时，最大续航时间为8小时，飞行时的转弯半径不小于100米，最大爬升(俯冲)角度为±15°，与其它障碍物(含地面)的安全飞行距离不小于50米，最大飞行高度为海拔5000米。所有无人机均按规划好的航路自主飞行，无须人工控制，完成任务后自动返回原基地。

三、简介

该题目中附件1中给出了震区的高程数据，这个数据包含三个维度：经度、纬度以及高度。matlab中最常用的展示三维数据的方式是画三维曲面，这一功能通过surf函数达到，效果如图1——

另外还可以通过等高线图描述三维数据，实际上是用颜色来表达高度这一维数据，使用matlab的contour函数可达到目的，效果如图2所示——

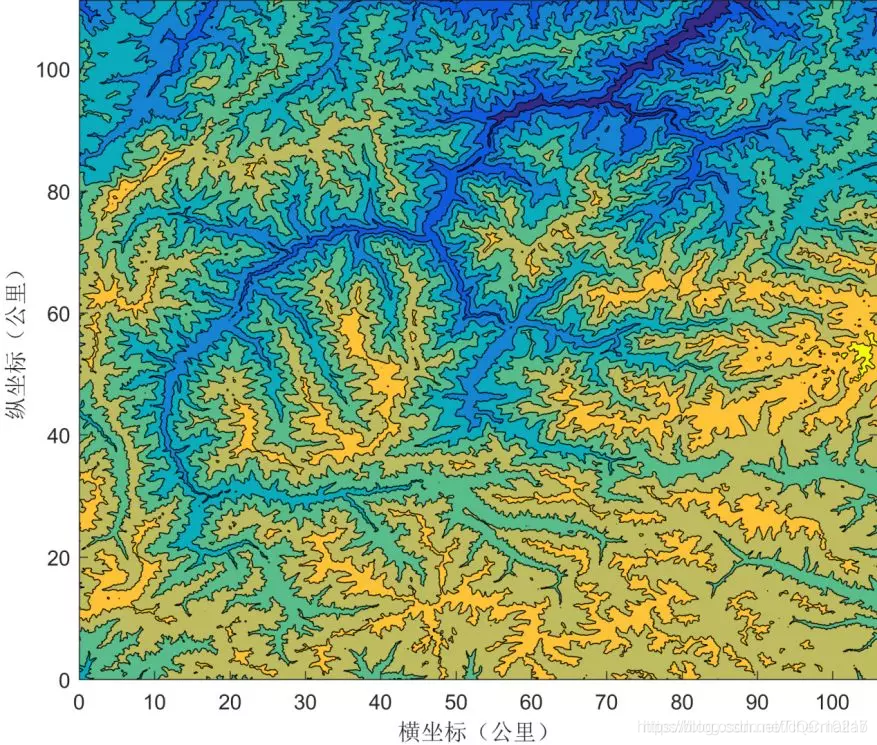
四、源代码

以下是实现三维地形图和等高图用到的代码——

function mainfun()

S1_rawdata=importdata('附件1 区域高程数据.xlsx');
S1_rawdata=S1_rawdata'/1000;
position_Keyareas =[30.3  89.8
66.0  84.7
98.4  76.7
73.7  61.0
57.9  47.6
86.8  22.0
93.6  48.8];

x=0:0.0382*10:2774*0.0382;
y=0:0.0382*10:2912*0.0382;

%三维地形图
[x,y]=meshgrid(x,y);
figure
surf(x,y,S1_rawdata(1:10:end,1:10:end))

xdata0=0:0.0382:2774*0.0382;
ydata0=0:0.0382:2912*0.0382;

figure
contour(xdata0,ydata0,S1_rawdata,[2.2,2.4,2.6,2.8,3,3.200,3.400,3.600,3.800,4.000,4.1500])
hold on
plot(110,0,'r>','MarkerFaceColor','r')
text(100,5,'基地H','Color','r')
centername={'A','B','C','D','E','F','G'};
t=0:0.1:2*pi;
xx=sin(t);
yy=cos(t);
for i=1:7
    plot(position_Keyareas(i,1),position_Keyareas(i,2),'ro','MarkerFaceColor','r')
    text(position_Keyareas(i,1)-3,position_Keyareas(i,2)+3,centername{i},'Color','r')
    plot(10*xx+position_Keyareas(i,1),10*yy+position_Keyareas(i,2),'r--')
end

%C平均海拔

mean(mean(S1_rawdata(2317:2837,1749:2269)))

contour(xdata0,ydata0,S1_rawdata,[3,4.150])
hold on
plot(110,0,'r>','MarkerFaceColor','r')
text(100,5,'基地H','Color','r')
centername={'A','B','C','D','E','F','G'};
t=0:0.1:2*pi;
xx=sin(t);
yy=cos(t);
for i=1:7
    plot(position_Keyareas(i,1),position_Keyareas(i,2),'ro','MarkerFaceColor','r')
    text(position_Keyareas(i,1)-3,position_Keyareas(i,2)+3,centername{i},'Color','r')
    plot(10*xx+position_Keyareas(i,1),10*yy+position_Keyareas(i,2),'r--')
end

for i=1:44
    for j=1:44
        line([2.5*i,2.5*i],[0,110])
        line([0,110],[2.5*i,2.5*i])
    end
end


  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
 

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]李昕.MATLAB数学建模[M].清华大学出版社.2017
[2]王健,赵国生.MATLAB数学建模与仿真[M].清华大学出版社.2016
[3]余胜威.MATLAB数学建模经典案例实战[M].清华大学出版社.2015

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/112792636