【元胞自动机】基于matlab元胞自动机双边教室疏散【含Matlab源码 1208期】

一、元胞自动机简介

1 元胞自动机发展历程
最初的元胞自动机是由冯 · 诺依曼在 1950 年代为模拟生物 细胞的自我复制而提出的. 但是并未受到学术界重视.
1970 年, 剑桥大学的约翰 · 何顿 · 康威设计了一个电脑游戏 “生命游戏” 后, 元胞自动机才吸引了科学家们的注意.

1983 年 S.Wolfram 发表了一系列论文. 对初等元胞机 256 种 规则所产生的模型进行了深入研究, 并用熵来描述其演化行 为, 将细胞自动机分为平稳型, 周期型, 混沌型和复杂型.

2 对元胞自动机的初步认识
元胞自动机（CA）是一种用来仿真局部规则和局部联系的方法。典型的元胞自动机是定义在网格上的，每一个点上的网格代表一个元胞与一种有限的状态。变化规则适用于每一个元胞并且同时进行。典型的变化规则，决定于元胞的状态，以及其（ 4 或 8 ）邻居的状态。

3 元胞的变化规则&元胞状态
典型的变化规则，决定于元胞的状态，以及其（ 4 或 8 ）邻居的状态。

4 元胞自动机的应用
元胞自动机已被应用于物理模拟，生物模拟等领域。

5 元胞自动机的matlab编程
结合以上，我们可以理解元胞自动机仿真需要理解三点。一是元胞，在matlab中可以理解为矩阵中的一点或多点组成的方形块，一般我们用矩阵中的一点代表一个元胞。二是变化规则，元胞的变化规则决定元胞下一刻的状态。三是元胞的状态，元胞的状态是自定义的，通常是对立的状态，比如生物的存活状态或死亡状态，红灯或绿灯，该点有障碍物或者没有障碍物等等。

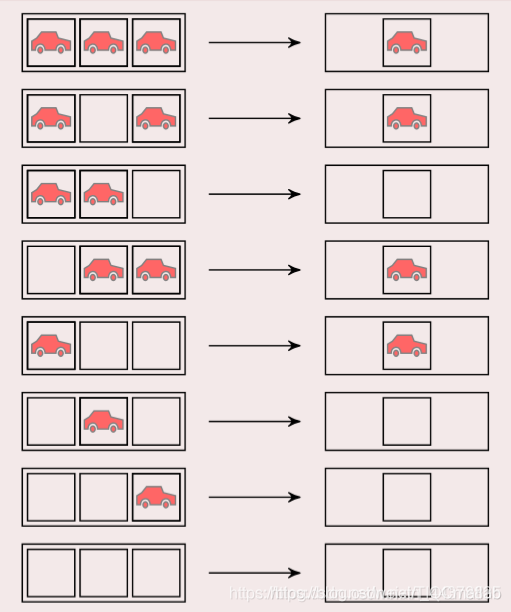
6 一维元胞自动机——交通规则
定义：
6.1 元胞分布于一维线性网格上.
6.2 元胞仅具有车和空两种状态.

7 二维元胞自动机——生命游戏
定义：
7.1 元胞分布于二维方型网格上.
7.2 元胞仅具有生和死两种状态.

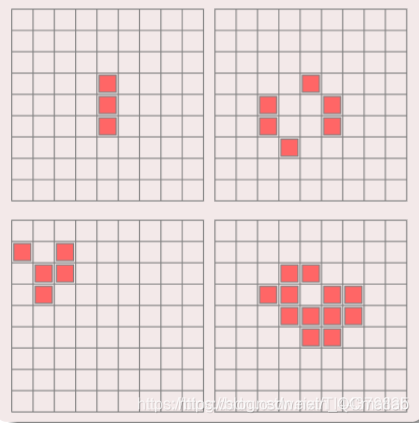
元胞状态由周围八邻居决定.
规则：

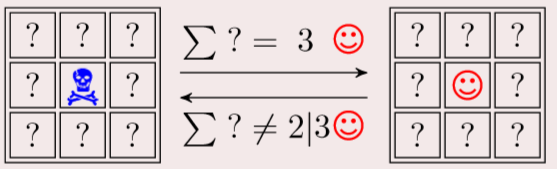
骷髅：死亡；笑脸：生存
周围有三个笑脸，则中间变为笑脸
少于两个笑脸或者多于三个，中间则变死亡。

8 什么是元胞自动机
离散的系统: 元胞是定义在有限的时间和空间上的, 并且元 胞的状态是有限.
动力学系统: 元胞自动机的举止行为具有动力学特征.
简单与复杂: 元胞自动机用简单规则控制相互作用的元胞 模拟复杂世界.

9 构成要素

（1）元胞 (Cell)

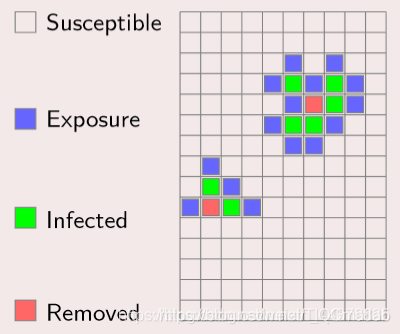
元胞是元胞自动机基本单元：
状态: 每一个元胞都有记忆贮存状态的功能.
离散: 简单情况下, 元胞只有两种可能状态; 较复杂情况下, 元胞具有多种状态.
更新: 元胞的状态都安照动力规则不断更新.
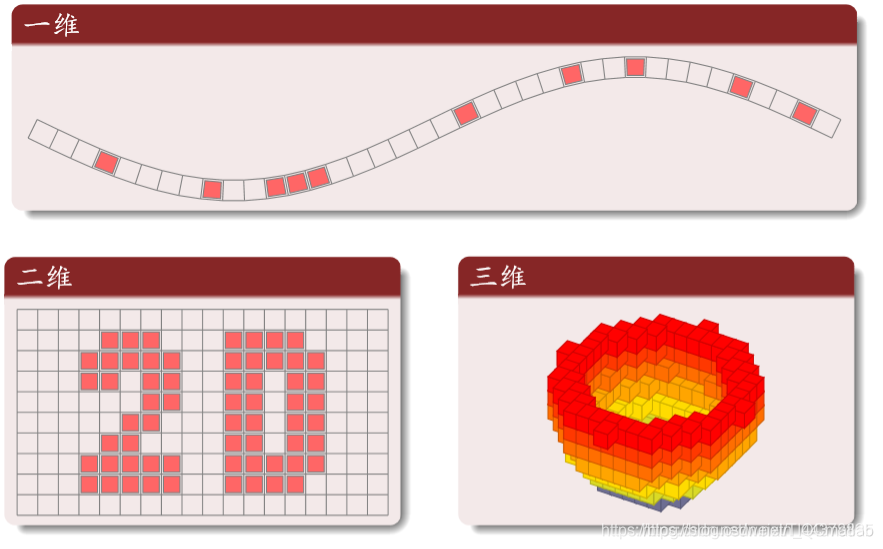
（2）网格 (Lattice)
不同维网格

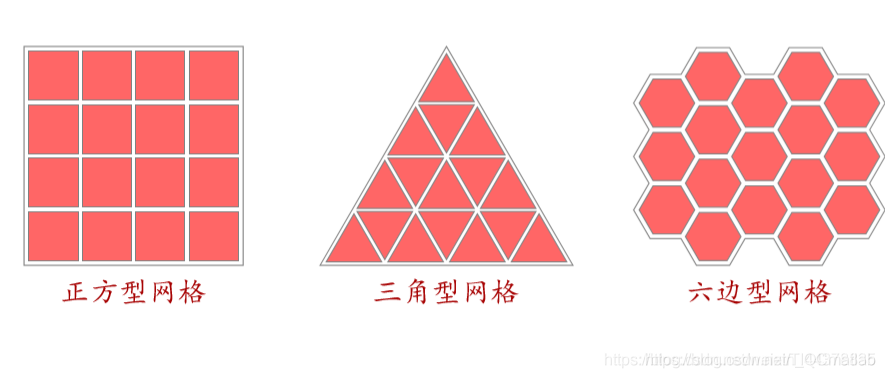
常用二维网格

（3）邻居 (Neighborhood)

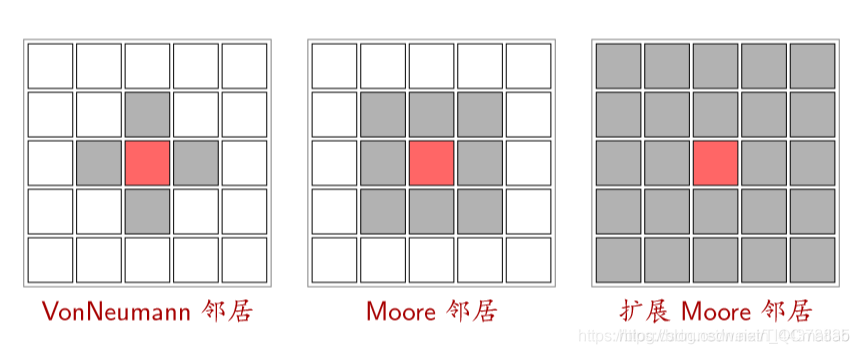
（4）边界 (Boundary)

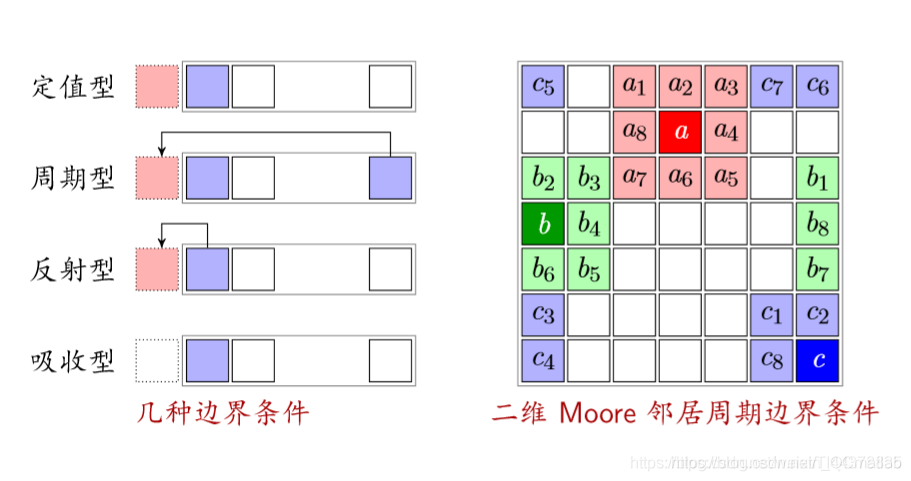
反射型：以自己作为边界的状态
吸收型：不管边界（车开到边界就消失）

（5）规则（状态转移函数）
定义：根据元胞当前状态及其邻居状况确定下一时刻该元胞状态的动力学函数, 简单讲, 就是一个状态转移函数.
分类 ：
总和型: 某元胞下时刻的状态取决于且仅取决于它所有邻居 的当前状态以及自身的当前状态.
合法型: 总和型规则属于合法型规则. 但如果把元胞自动机 的规则限制为总和型, 会使元胞自动机具有局限性.
（6）森林火灾

绿色：树木；红色：火；黑色：空地。
三种状态循环转化：
树：周围有火或者被闪电击中就变成火。
空地：以概率p变为树木
理性分析：红为火；灰为空地；绿是树

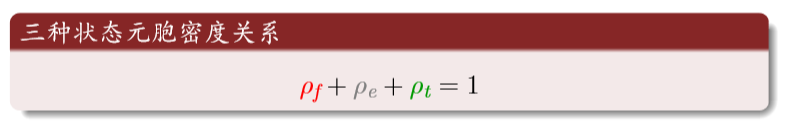
元胞三种状态的密度和为1

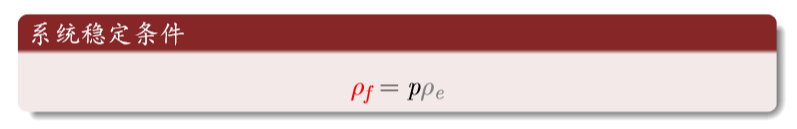
火转化为空地的密度等于空地转换为树的密度（新长出来的树等于烧没的树）

f是闪电的概率:远远小于树生成的概率；T s m a x T_{smax}T smax
​是一大群树被火烧的时间尺度
程序实现
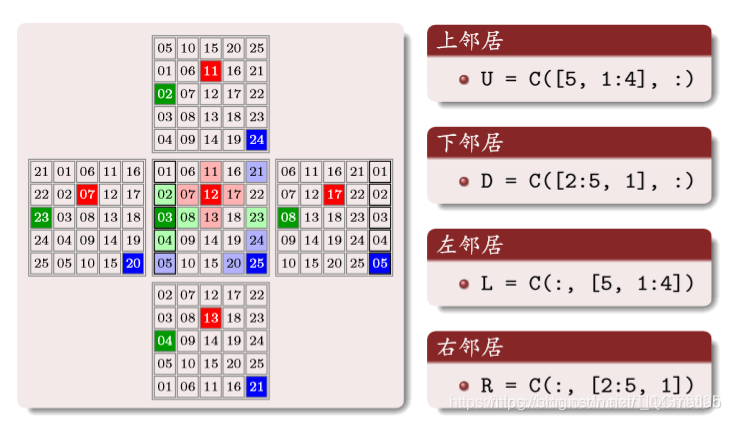
周期性边界条件
购进啊

其中的数字为编号
构建邻居矩阵

上面矩阵中的数字编号，对应原矩阵相同位置编号的上邻居编号，一 一对应
同样道理：

（7）交通概念
车距和密度

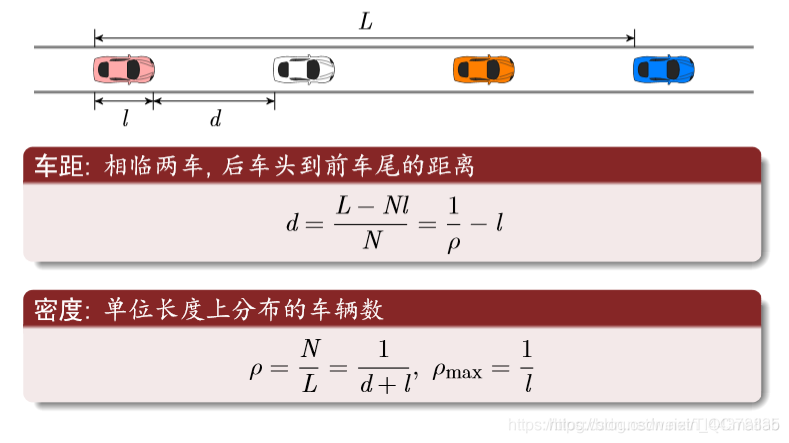
流量方程

守恒方程

时空轨迹（横轴是空间纵轴为时间）

红线横线与蓝色交点表示每个时间车的位置。
如果是竖线则表示车子在该位置对应的时间

宏观连续模型：

最常用的规则：

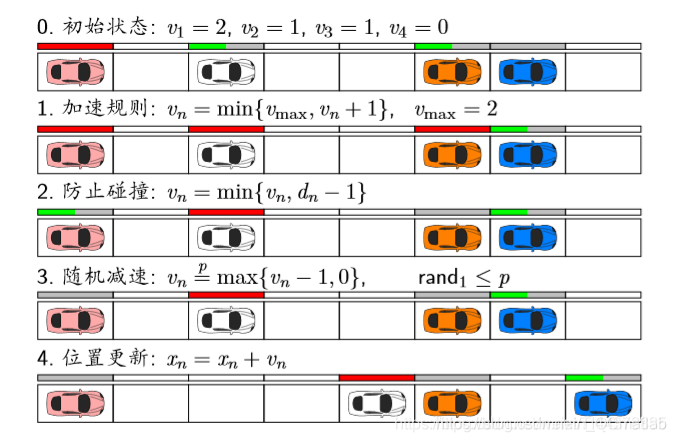
红色条表示速度是满的。

1 加速规则：不能超过v m a x （ 2 格 / s ） v_{max}（2格/s）v
max（2格/s）
2 防止碰撞：不能超过车距

理论分析：

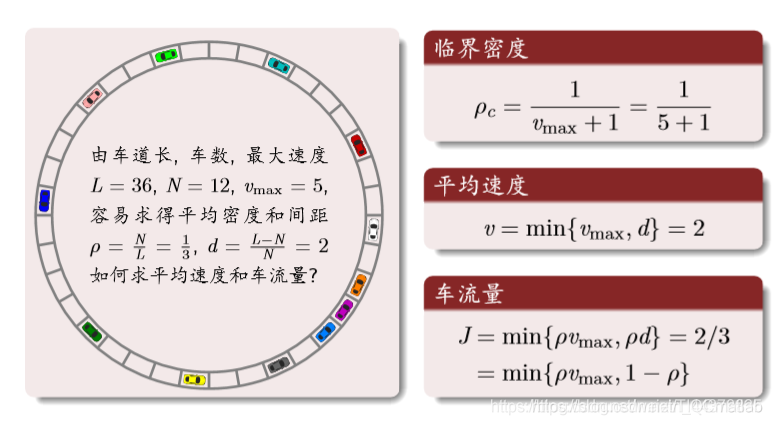
结果分析: 密度与流量

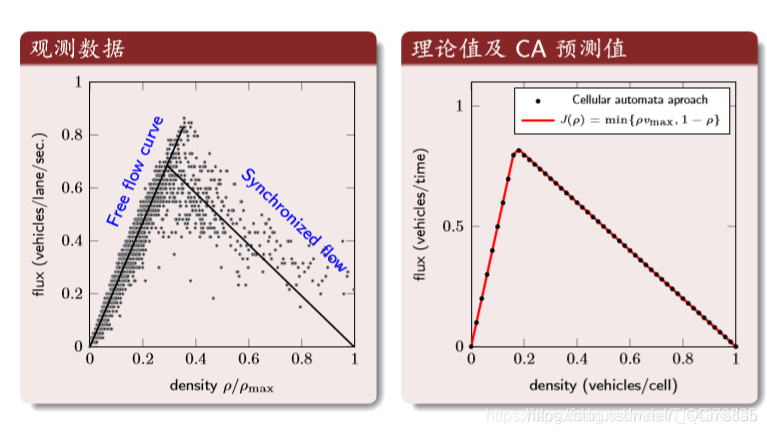
第一个图：横坐标是归一化后的密度，纵坐标是车流量。第二个图：理论值与CA的结果

结果分析: 时空轨迹

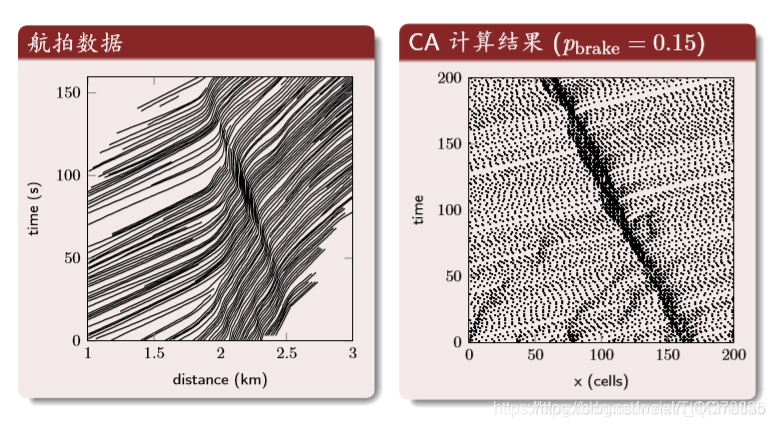
中间的深色区域是交通堵塞的区域。

二、部分源代码

% 将TheSeed模型房间内障碍物和门固定了下来，将其划分为几个小房间，其余没有改动
% calculates static field - returns computed static field
% input:
% n - x dimension
% m - y dimension
% doors - array of doors - each row represents one door cell and consist of two columns - (i,j) coords
% doorLengths - array, containd lengths of each door
% contraction - effective DoorLength/doorLength
% nObstacles - number of obstacles. Necassary, because matlab don't know how to pass array with zero length
% Ks - influence for door field
% Kw - influence of wall field
% pI - 惯性因子=exp(kI)，kI是灵敏度因子。
% pW - wall potential，人群移动时会避免靠近障碍物和墙体

function main()

GridDims=[50,50];                % 设置房间大小，因为一个单位0.5m，所以这里代表的是11m*5m大小的房间，一面墙体也占用了一个单元
population=500;                   % 设置人数



nDoors=1;                        % 这个参数在本模型中已经用不上了
doorLengths=[6];


% nObstacles=5;                    % 这两行东西的设置我也要看看还需不需要保留


Ks=1000;
Kw=3;

alpha=0.8;
delta=0.8;
miu=0.1;

contraction=0.6;                 % 这个东西。。用来表示宽出口的收缩，我也不理解这个的作用

% paramsDoors=[nDoors,lengths];
[Occupied,Doors,Obstacles]=populate(population,GridDims);
params=[Ks,Kd,alpha,delta,miu,Ki];

% StatField=ones(GridDims(1),GridDims(2));    % alerady in exponenta
% 上面这一行有什么用？在calcStatField函数里面就又先令为0了

DynField=zeros(GridDims(1),GridDims(2));

if(Ks)
    StatField=calcStatField(GridDims, Doors, doorLengths, contraction, Obstacles, Ks, Kw);     % The Seed版的，没有过多修改
%     StatField=myCalcStatField(GridDims,Occupied,Doors,lengths,contraction,nObstacles,population,Ks, Kw);
end

%movie object to record
mov=VideoWriter('output.avi');   
open(mov);



cnt = 0;
evacuated = 0;
while( (evacuated ~= population))
cnt = cnt + 1;
draw(Occupied);
F = getframe(fig);
writeVideo(mov,F);
pause(0.1)                                % 每一步的停顿间隔
[Occupied, DynField, cur_evacuated] = myUpdate(Occupied, DynField, StatField, params);
evacuated = evacuated + cur_evacuated;
end

draw(Occupied);

close(mov);
disp(cnt);                                 % 计时
end
% 计算S场，这个是基于The Seed，基本上没有改动的版本
% 在The Seed里面，表面上将Doors定义为nDoors行2列的矩阵，实际上Doors是宽度行2列的矩阵。
% 例如，只有一个宽度为7的横向的门，则Doors是7行2列的矩阵，每一行对应于门的一个cell。
function StatField = calcStatField(GridDims, Doors, doorLengths, contraction, obstacles, Ks, Kw)

n = GridDims(1);
m = GridDims(2);
nDoors = size(doorLengths);

% if nObstacles ~= 0                             % 这三行是用来干吗的？我注释掉他们程序一样能跑。
% nObstacles = size(obstacles);                  % 我这里对于障碍物的定义没有那么简单，因此，我觉得可能我需要做一些修改
% end

StatField = zeros(n, m);                       % 初始化为50*50的0阵
maxDist = 0;

for i = 2: n-1
for j = 2: m-1
minDist = inf;                                 % inf是无穷大
% 找到到出口的最短路径

cnt = 1;
for k = 1: nDoors

% 这两步我是没理解的，有效宽度是什么？什么依据？
effectiveLength = contraction*doorLengths(k);                  % 有效宽度  contraction = 0.6  doorLengths的取值范围[5,10]
offset = floor((doorLengths(k)-effectiveLength) * 0.5);       % floor(x)是将其化为小于等于x的最大整数。offset的取值范围[1,2].

% 这个for是为了找到这个(i,j)到对应的这个门最近的距离。
for l = offset: offset + effectiveLength-1                    % 这个地方的l是小写的L！有小数也无所谓，循环的时候取的是整数。

% power(a,b)是a中每个元素的b次幂。po表示(i,j)到门的距离的平方。
po = power((i-Doors(cnt+l, 1)),2)+power((j-Doors(cnt+l,2)), 2);  % doors(cnt+l,1)就是门的i坐标，doors(cnt+l,2)是门的j坐标
% （这个地方加的是小写的L，不是1）cnt+l是因为：这里计算的是(i,j)到门之间有多少格，所以+l.

% 如果门不可见，它的距离大于直线，因此超过minDist
if(po >= minDist)                                             % 目的在于找到最小的Dist
continue;
end

% check if there is visible path to doors
% TODO:

minDist = po;                                                 % 这样就不是无穷大了
end
cnt = cnt + doorLengths(k);
end

StatField(i, j) = minDist;
if(maxDist < minDist)
maxDist = minDist;                                              % 找出整个房间里面，距离门最远的距离
end
end
end
dMax = 4;        % 墙的影响半径

StatField(1,:) = -1;       %不管这里有什么
StatField(n,:) = -1;
StatField(:,1) = -1;
StatField(:,m) = -1;

for i = 2: n-1
for j = 2: m-1
    %门的吸引力
    %if(maxDist == StatField(i,j))
%StatField(i,j) = 0;
%else             %exp(Ks/(1-sqrt(maxDist/StatField(i,j)))); 
StatField(i,j) = Ks*exp(-StatField(i,j)/maxDist*750);
%end     上面的距离实际上都是平方了过后的，我还需要考察需不需要把它开方回来
% find min dist to the obstacle 
minDistObst = inf; 
nObstacles = 0; 
for l = 1: nObstacles 
    po = power((i-obstacles(l, 1)),2)+power((j-obstacles(l,2)), 2); 
    if(po < minDistObst) 
        minDistObst = po; 
    end 
end 
%StatField(i,j) = 1;      % for visualization of repulsive wall field 
% repulsive potential of walls 
if(minDistObst ~= inf) 
    if(minDistObst == 0) 
        StatField(i,j) = 0; 
        continue; 
    end

minDistObst = sqrt(minDistObst); 
if(minDistObst < dMax) 
    StatField(i,j) = StatField(i,j)*exp(Kw*(1-(dMax/minDistObst))); 
end
end
end
end
end

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
  
107
  
108
  
109
  
110
  
111
  
112
  
113
  
114
  
115
  
116
  
117
  
118
  
119
  
120
  
121
  
122
  
123
  
124
  
125
  
126
  
127
  
128
  
129
  
130
  
131
  
132
  
133
  
134
  
135
  
136
  
137
  
138
  
139
  
140
  
141
  
142
  
143
  
144
  
145
  
146
  
147
  
148
  
149
  
150
  
151
  
152
  
153
  
154
  
155
  
156
  
157
  
158
  
159
  
160
  
161
  
162
  
163
  
164
  
165
  
166
  
167
  
168
 

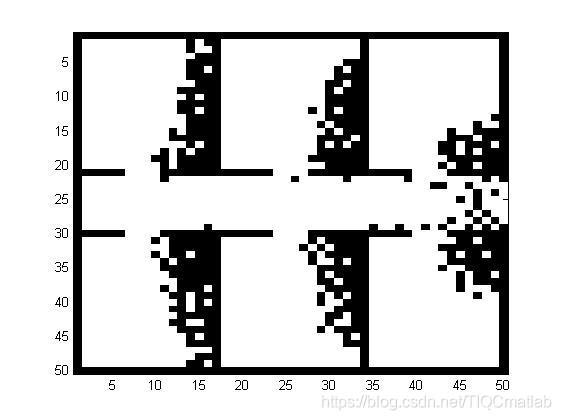
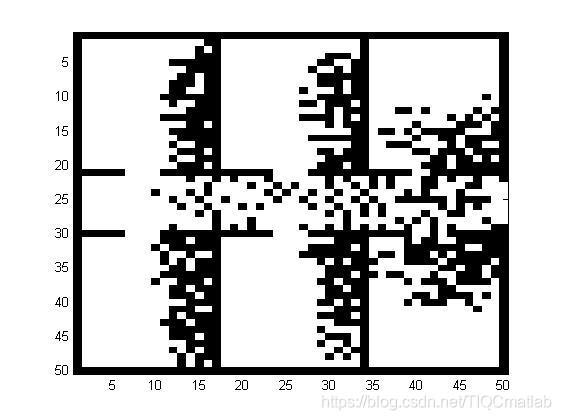
三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]【数学建模】元胞自动机.博主：二进制 人工智能

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/119567865