数字信号处理之期中斩神篇（四重 斩仙）

DFT对连续信号进行谱分析

        信号的谱分析，就是计算信号的傅里叶变换，连续信号与系统的傅里叶分析不便于直接用计算机进行计算。 DFT是一种时域和频域均离散化的变换，DFT适合数值计算，得到广泛应用。对连续时间和系统，可通过时域采样，应用DFT进行近似谱分析。

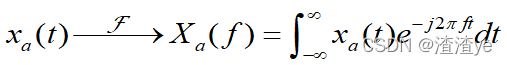
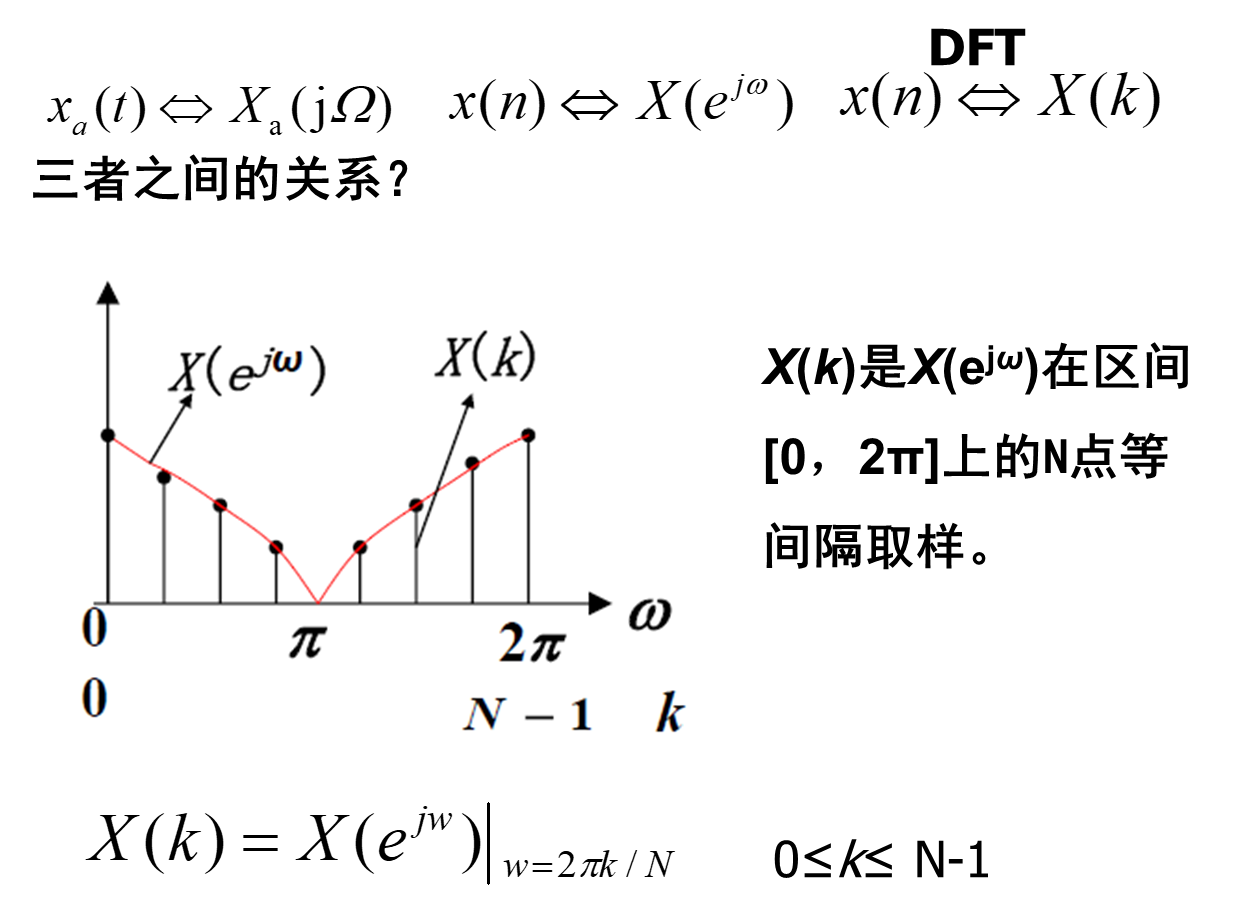
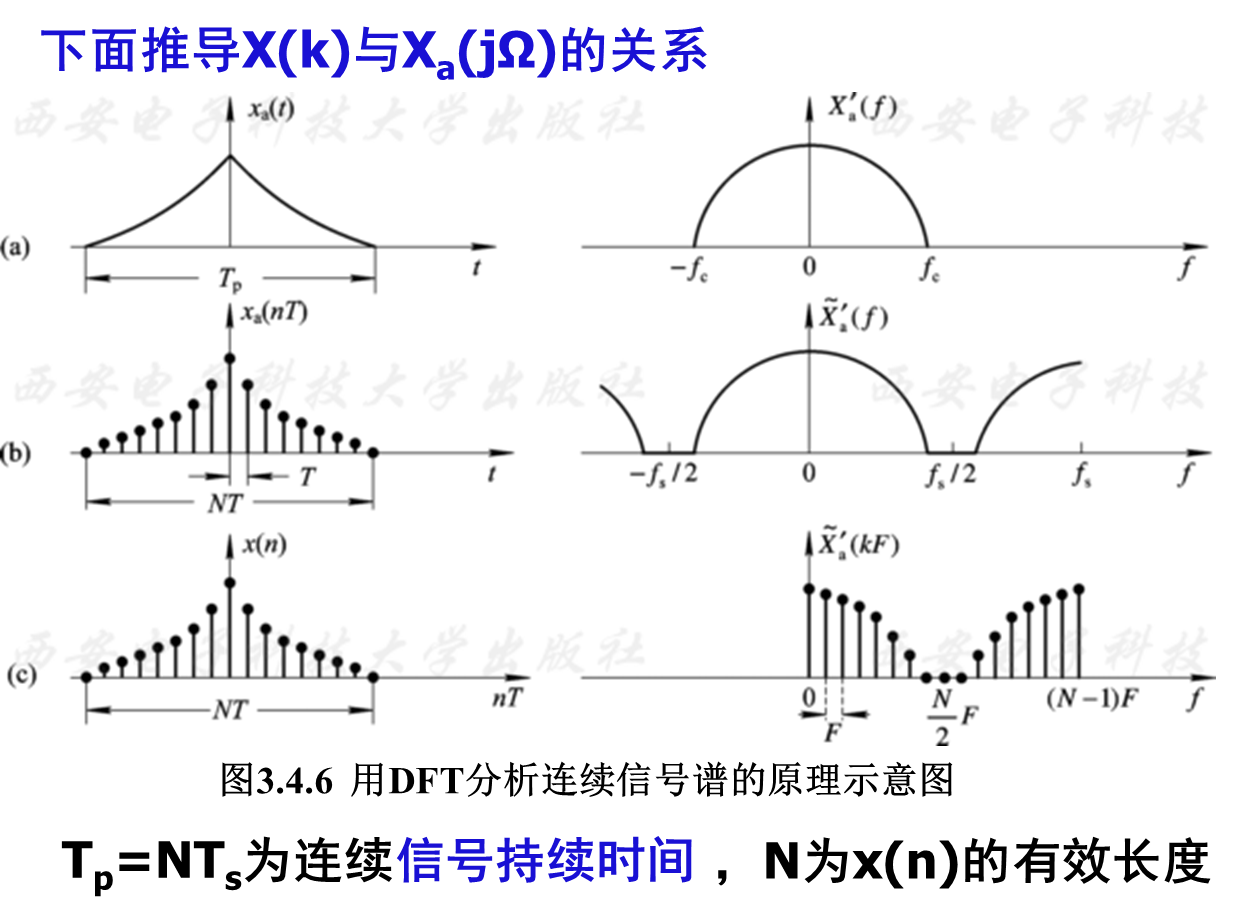
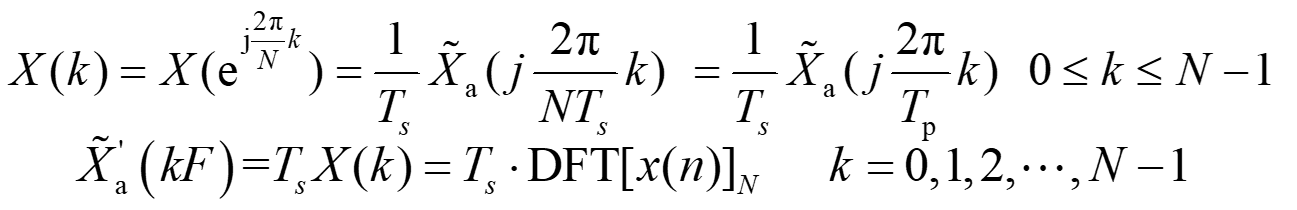
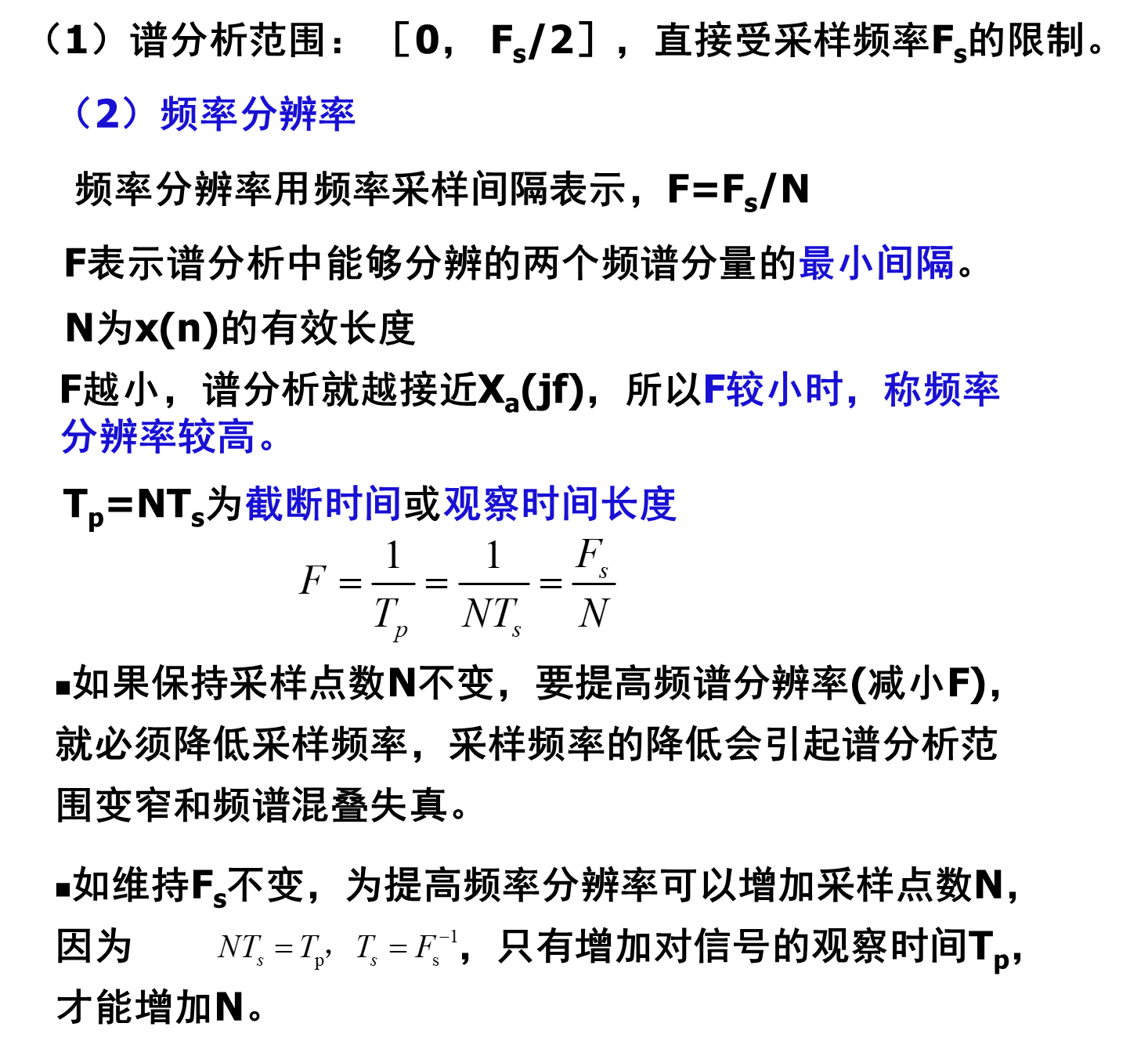
频率分辨率

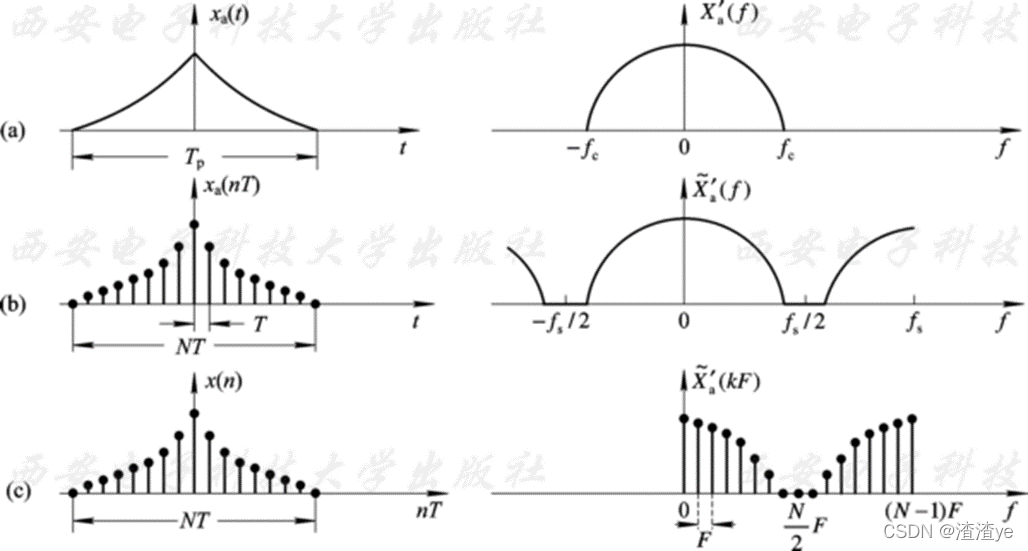
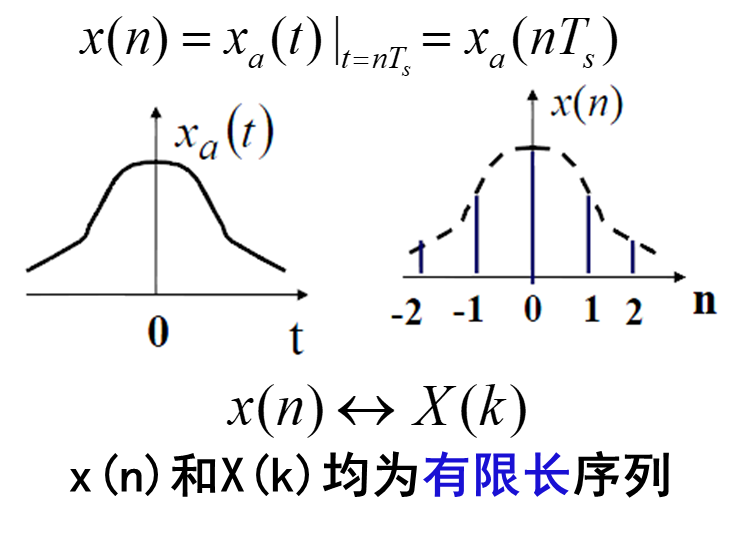
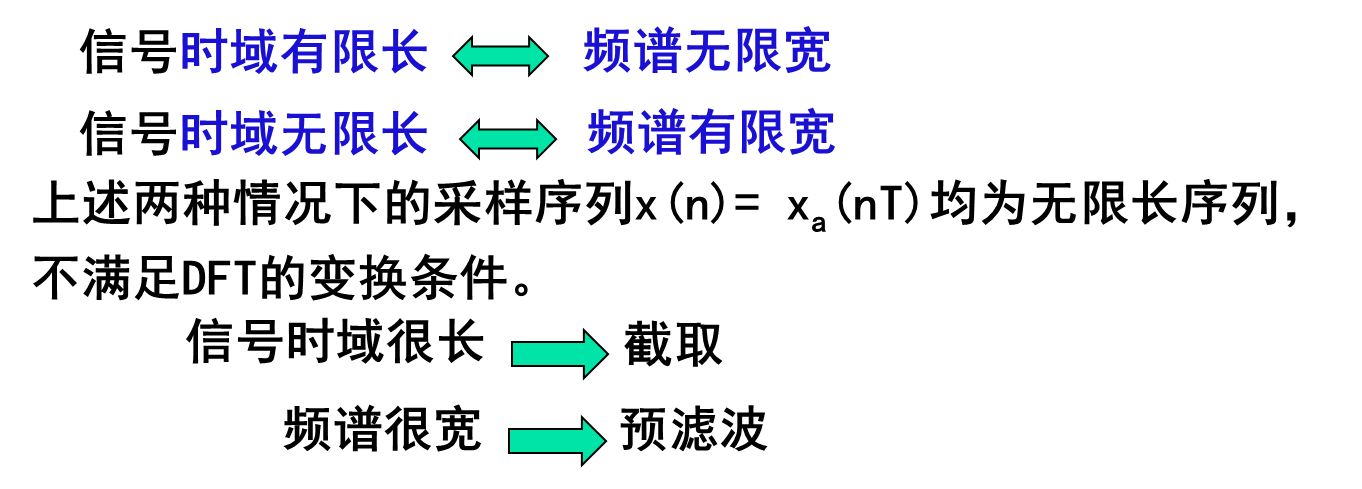
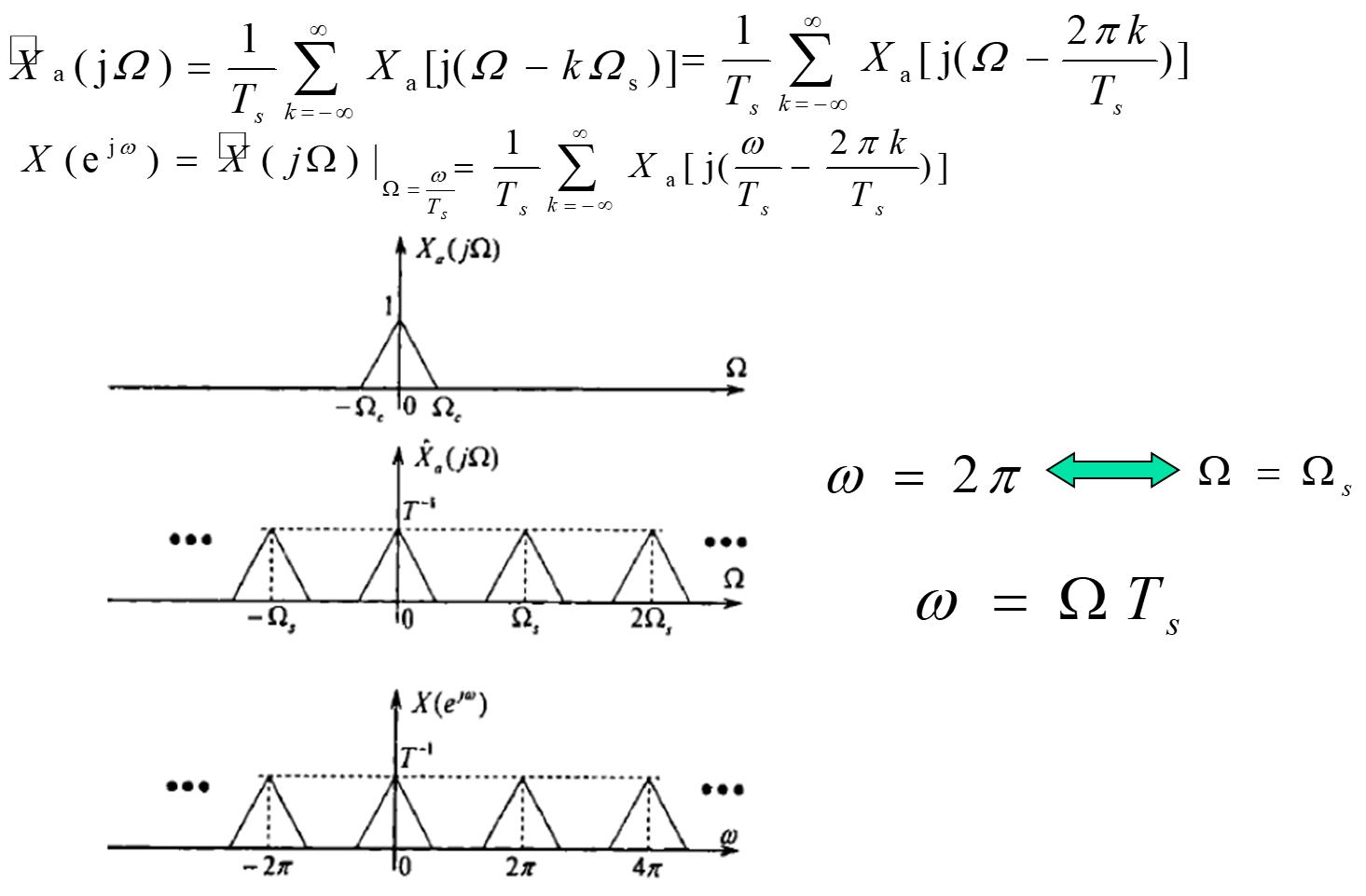
可通过对连续信号采样并进行DFT再乘以Ts，近似得到模拟信号频谱的周期延拓函数在第一个周期［0，Fs］上的N点等间隔采样

对满足假设的持续时间有限的带限信号，在满足时域采样定理时， 包含了模拟信号频谱的全部信息（k=0, 1, 2, …, N/2, 表示正频率频谱采样；k=N/2+1，N/2+2，…，N－1, 表示负频率频谱采样。

对实信号，其频谱函数具有共轭对称性，分析正频率频谱即可。不存在频谱混叠失真时，正频率［0，Fs/2］频谱采样为

谱分析范围、频率分辨率

例题

DFT对连续信号进行谱分析时参数选择原则

例题

说明： 为提高谱分辨率，又保持谱分析的范围不变（ Fs 采样频率不变），只能增长纪录时间Tp（截取长度），增加采样点数N。

误差问题：

（1）混叠现象

（2）栅栏效应

（3）截断效应--泄漏

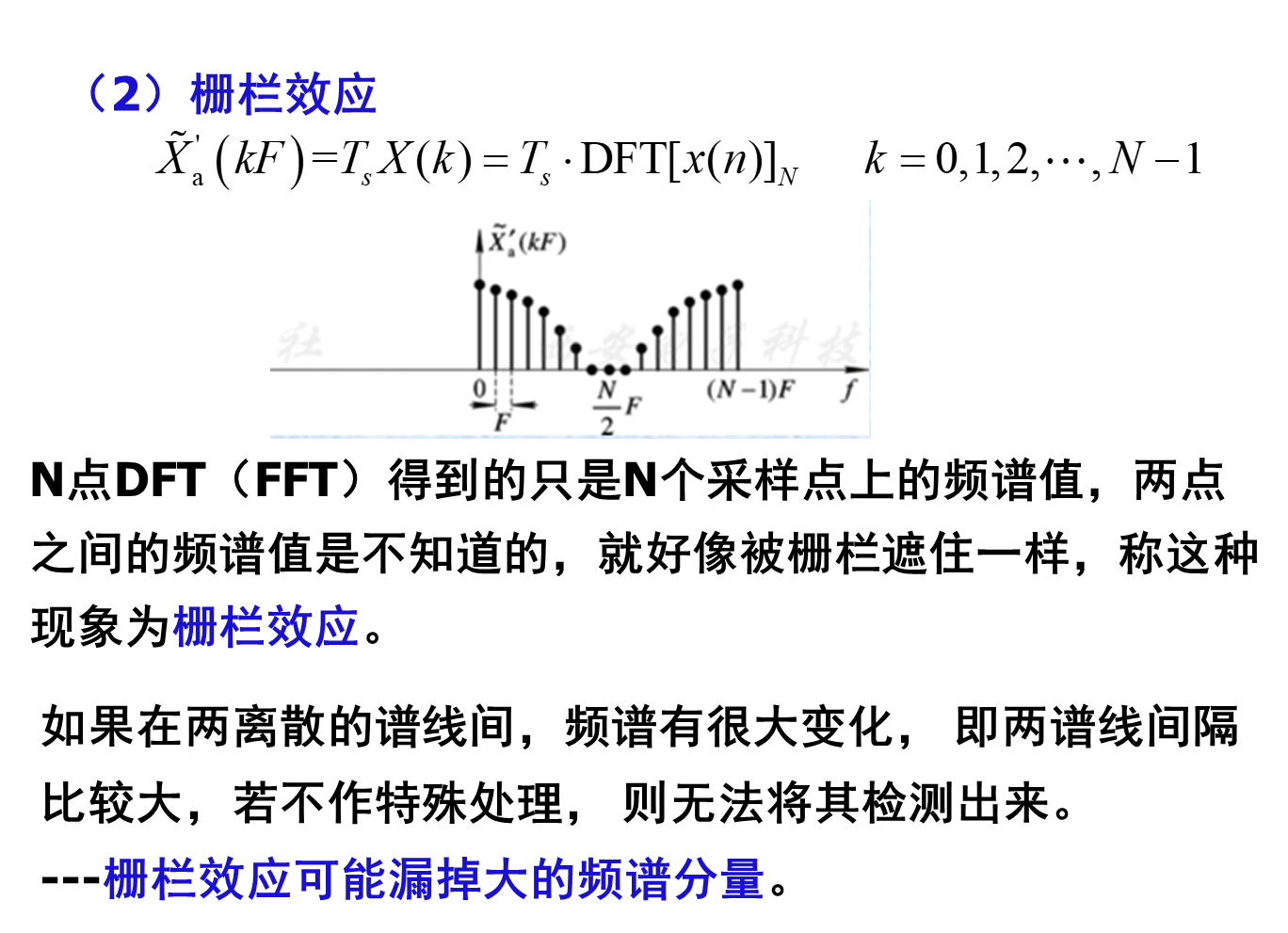
如何使原来漏掉的某些频谱分量被检测出来：

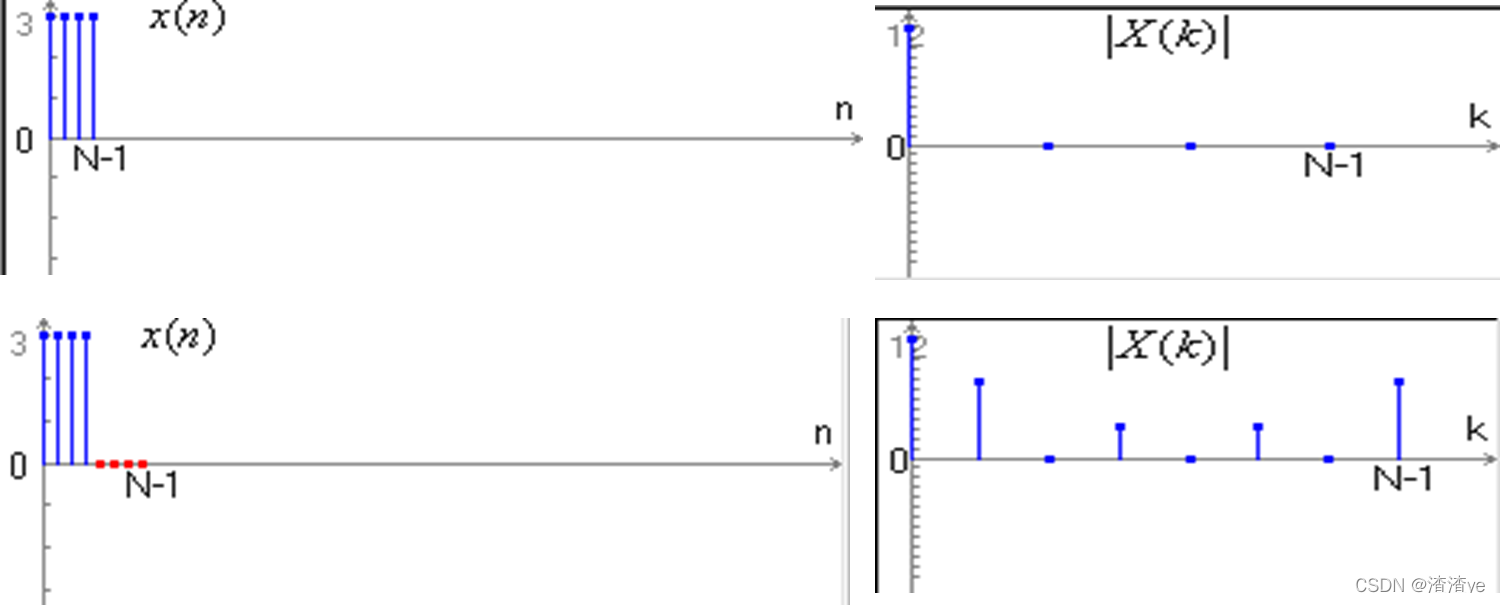
1.减小栅栏效应的一个方法是在所取数据的末端加一些零值点(时域),使一个周期内点数增加,但是不改变原有的记录数据。

2.N变大，频域抽样间隔变小,从而能保持原来频谱形式不变的情 况下使谱线变密,也就使频谱抽样点数增加。

3.这样,就有可能看到原来看不到的频谱分量。 

 时域补加零值点后对频域的影响

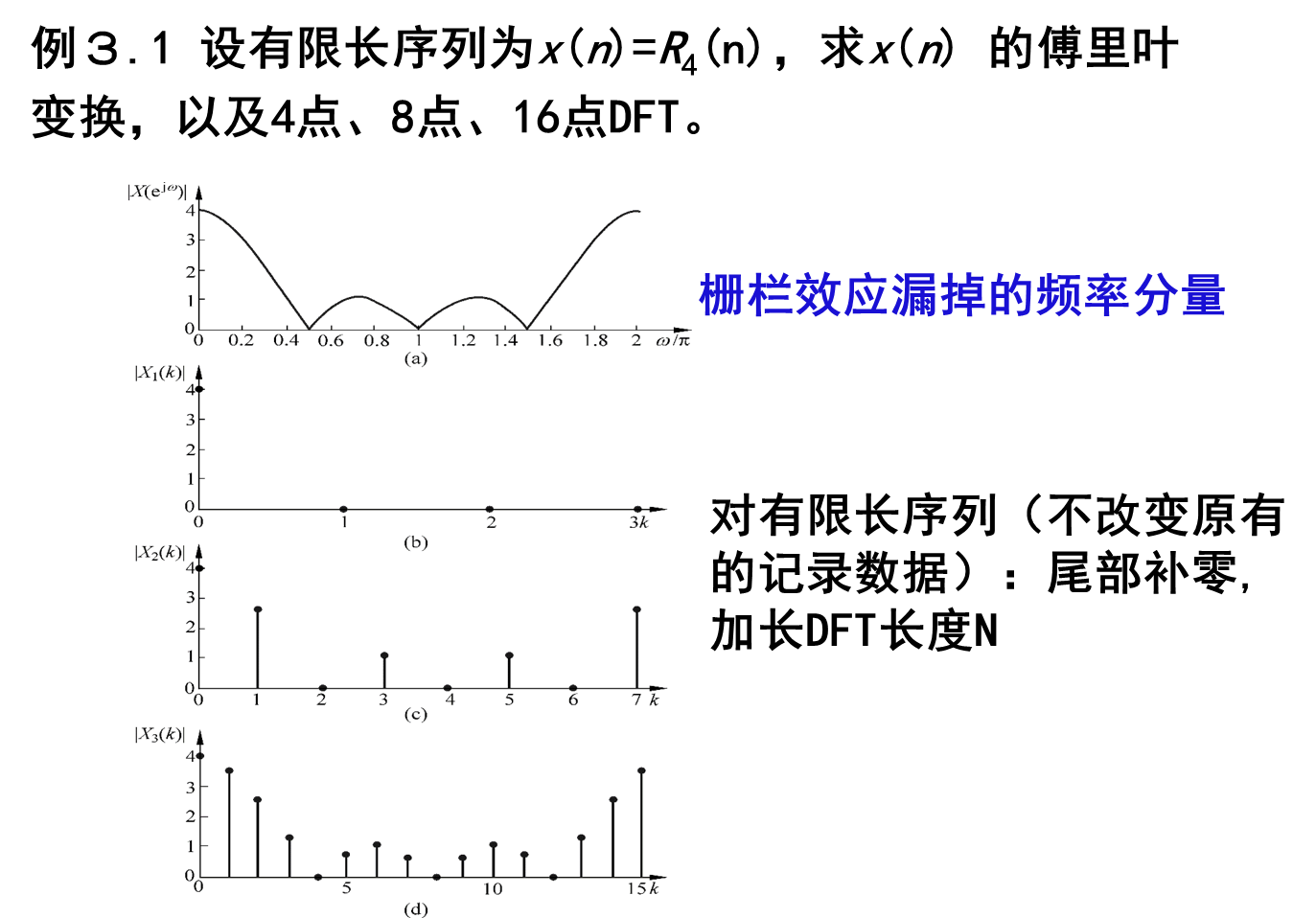
例题

截取

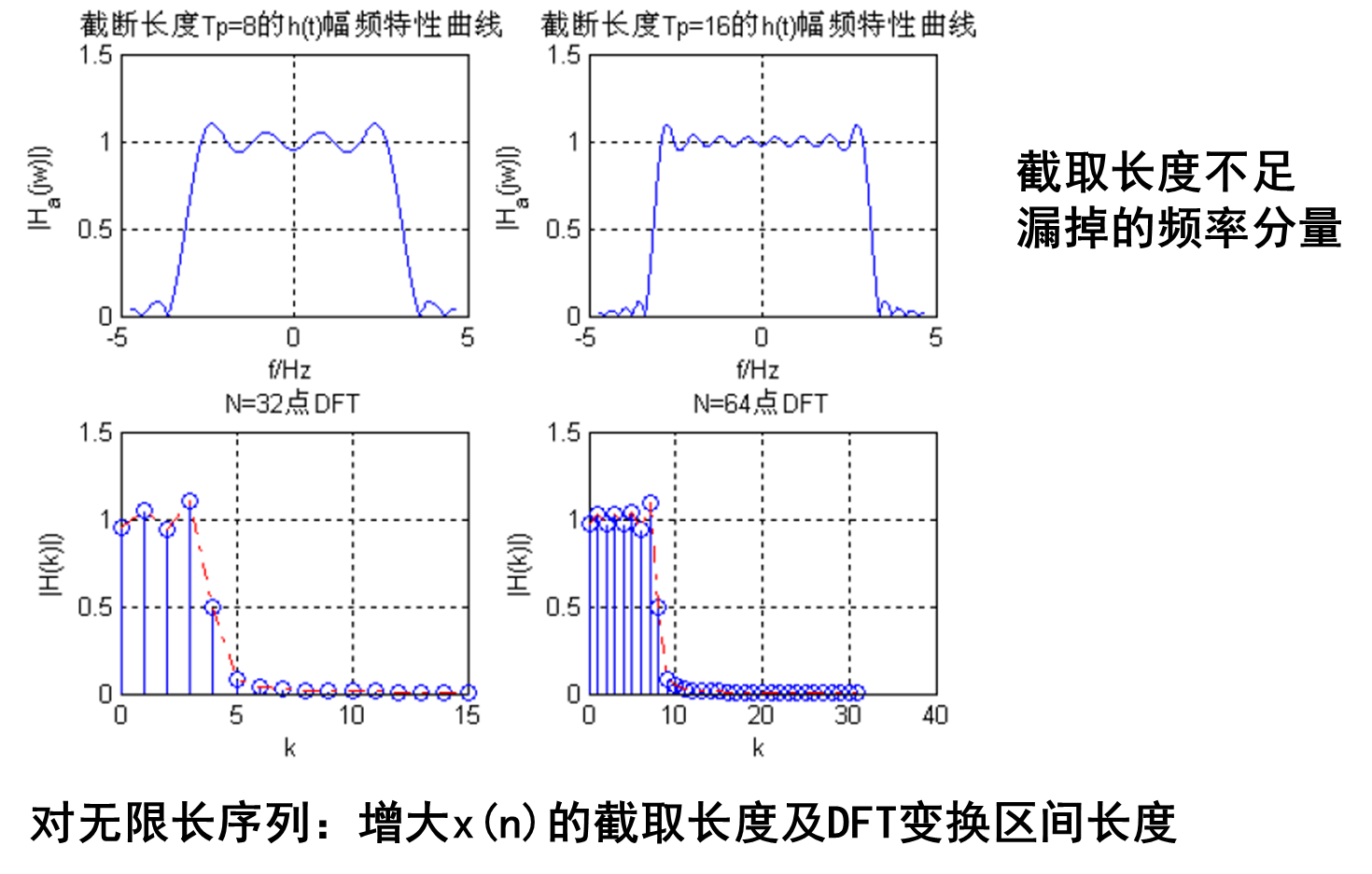
小总结

有限长序列：尾部补零  补零加长DFT的长度N

无限长序列：增大x(n)的截取长度及DFT变换区间长度

 截取加长DFT变换区间长度N

以此增加频域采样点数和采样点位置，使原来漏掉的某些频谱分量可能被检测出来。

截断效应

对无限长的信号进行截断而引起的误差现象称为截断效应

采样序列x(n)，对它用长为N的窗函数进行截断

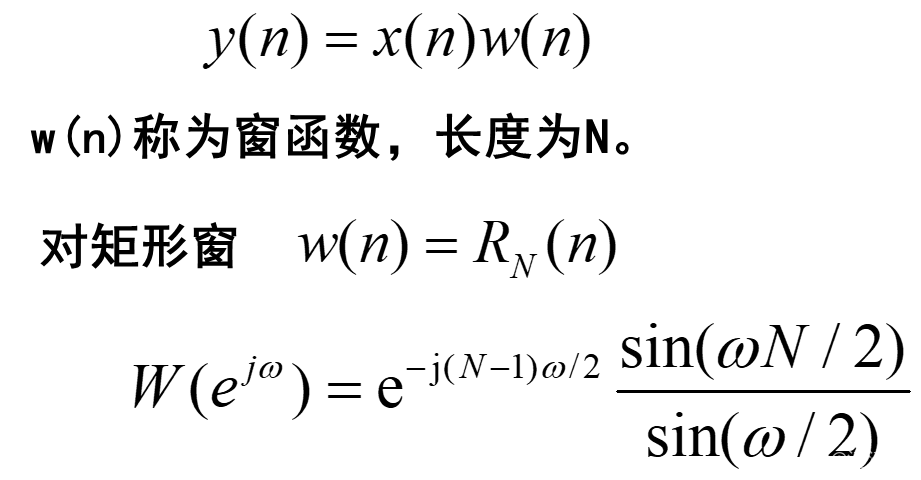
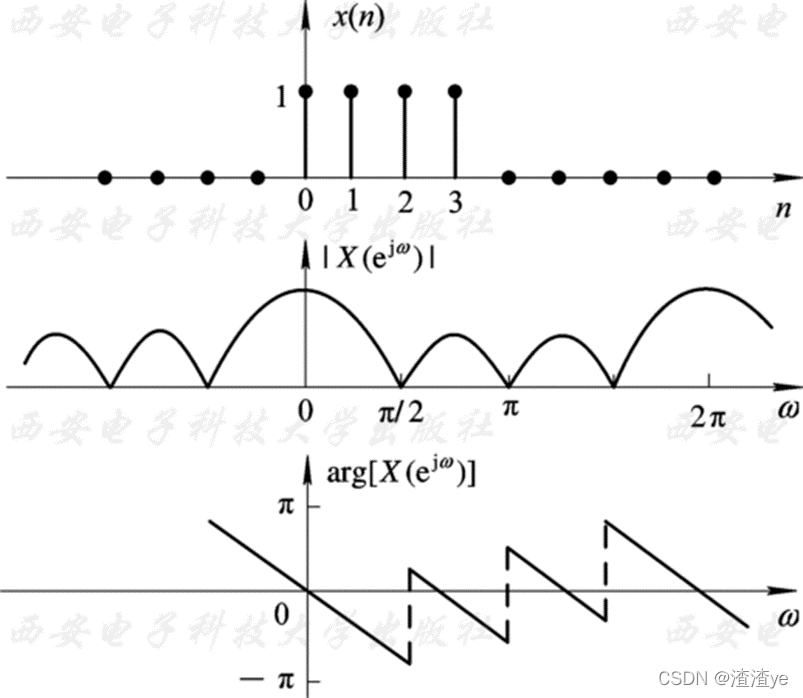
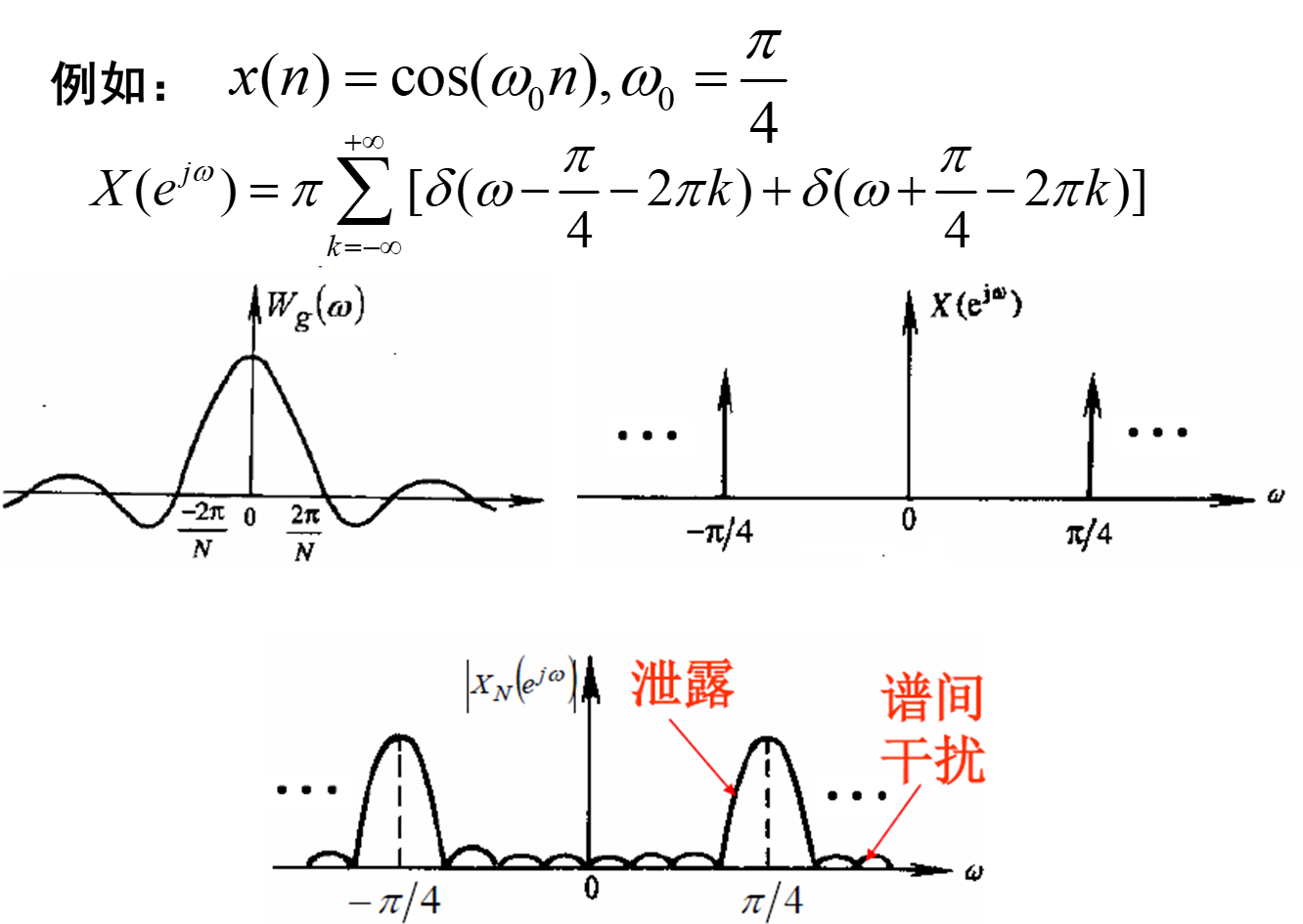
比较截断前、后的幅度谱的差别：——截断效应

(1)泄露:频谱成分从处“泄露”到 其他频率处   

定义：原来的离散谱线向附近展宽，这种将谱线展宽的现象称为频谱泄漏。

影响：泄漏会使频谱变模糊，谱的分辨率降低。

出现原因：与主瓣宽度直接相关

应对措施：适当加大窗口宽度，增加截短长度N。

(2)谱间干扰

影响：引起不同频率分量间的干扰，降低谱分辨率

出现原因：频谱卷积以后存在着的旁瓣

应对措施：选择其他形状的窗函数代替矩形窗

文章来源: blog.csdn.net，作者：渣渣ye，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/yyfloveqcw/article/details/123965630