sklear多项式回归
【摘要】 来源:
https://www.icourse163.org/course/BIT-1001872001
多项式回归
多项式回归(Polynomial Regression)是研究一个因变量与一 个或多个自变量间多项式的回归分析方法。如果自变量只有一个 时,称为一元多项式回归;如果自变量有多个时,称为多元多项 式回归。
一元m次多项式回归方程为:
二元二...
来源:
https://www.icourse163.org/course/BIT-1001872001
多项式回归
多项式回归(Polynomial Regression)是研究一个因变量与一 个或多个自变量间多项式的回归分析方法。如果自变量只有一个 时,称为一元多项式回归;如果自变量有多个时,称为多元多项 式回归。
- 一元m次多项式回归方程为:

- 二元二次多项式回归方程为:

- 在一元回归分析中,如果依变量y与自变量x的关系为非线性的,但 是又找不到适当的函数曲线来拟合,则可以采用一元多项式回归。
- 多项式回归的最大优点就是可以通过增加x的高次项对实测点进行逼 近,直至满意为止。
- 事实上,多项式回归可以处理相当一类非线性问题,它在回归分析 中占有重要的地位,因为任一函数都可以分段用多项式来逼近。
不同于线性回归, 多项式回归是使用曲线拟合数据的 输入与输出的映射关系
文章来源: maoli.blog.csdn.net,作者:刘润森!,版权归原作者所有,如需转载,请联系作者。
原文链接:maoli.blog.csdn.net/article/details/90606243
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者

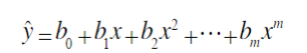
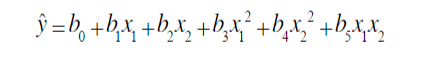

评论(0)