用dfs在带权树网络中统计可连接服务器对数目

举报
Xxy_1008 发表于 2024/08/28 16:43:24 2024/08/28
【摘要】 深度优先搜索（Depth-First Search，简称 DFS）是一种用于遍历或搜索树或图的算法。其核心思想是尽可能深地访问节点，然后再回溯。DFS 可以用于解决许多计算机科学问题，如路径查找、连通分量、拓扑排序等。DFS 的基本概念DFS 可以用递归或迭代（借助栈）来实现。无论哪种实现方式，DFS 的基本步骤都是相同的：访问当前节点。标记当前节点为已访问。递归或迭代地访问当前节点的每一个...

深度优先搜索（Depth-First Search，简称 DFS）是一种用于遍历或搜索树或图的算法。其核心思想是尽可能深地访问节点，然后再回溯。DFS 可以用于解决许多计算机科学问题，如路径查找、连通分量、拓扑排序等。

DFS 的基本概念

DFS 可以用递归或迭代（借助栈）来实现。无论哪种实现方式，DFS 的基本步骤都是相同的：

  1. 访问当前节点。
  2. 标记当前节点为已访问。
  3. 递归或迭代地访问当前节点的每一个未访问的邻居节点。

DFS 的实现方法

递归实现

在递归实现中，函数会调用自身来实现深度优先的遍历。


def dfs_recursive(graph, start, visited=None):
    if visited is None:
        visited = set()
    
    visited.add(start)
    print(start)  # 访问节点
    
    for neighbor in graph[start]:
        if neighbor not in visited:
            dfs_recursive(graph, neighbor, visited)

# 示例用法
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

dfs_recursive(graph, 'A')

迭代实现

在迭代实现中，使用栈来模拟递归调用的过程。



def dfs_iterative(graph, start):
    visited = set()
    stack = [start]
    
    while stack:
        node = stack.pop()
        if node not in visited:
            visited.add(node)
            print(node)  # 访问节点
            # 将邻居节点压入栈中
            stack.extend(reversed(graph[node]))

# 示例用法
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

dfs_iterative(graph, 'A')

应用场景

1. 路径查找

DFS 可以用于在图中查找从起始节点到目标节点的路径。



def dfs_path(graph, start, goal, path=None):
    if path is None:
        path = [start]
    if start == goal:
        return path
    for neighbor in graph[start]:
        if neighbor not in path:
            new_path = dfs_path(graph, neighbor, goal, path + [neighbor])
            if new_path:
                return new_path
    return None

# 示例用法
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

print(dfs_path(graph, 'A', 'F'))  # 输出 ['A', 'C', 'F']

2. 检测连通分量

DFS 可以用于检测图中的连通分量，即图中的所有节点是否连通。


def connected_components(graph):
    visited = set()
    components = []
    
    for node in graph:
        if node not in visited:
            component = []
            dfs_component(graph, node, visited, component)
            components.append(component)
    
    return components

def dfs_component(graph, node, visited, component):
    visited.add(node)
    component.append(node)
    for neighbor in graph[node]:
        if neighbor not in visited:
            dfs_component(graph, neighbor, visited, component)

# 示例用法
graph = {
    'A': ['B'],
    'B': ['A', 'D'],
    'C': ['E'],
    'D': ['B'],
    'E': ['C'],
    'F': []
}

print(connected_components(graph))  # 输出 [['A', 'B', 'D'], ['C', 'E'], ['F']]

时间复杂度和空间复杂度

  • 时间复杂度：DFS 的时间复杂度为 O(V + E)，其中 V 是顶点的数量，E 是边的数量。每个节点和边都被访问一次。
  • 空间复杂度：在最坏情况下，递归实现的空间复杂度为 O(V)，因需要存储递归调用栈。如果使用迭代实现，空间复杂度为 O(V)，因需要存储栈或队列。

Sum up：

DFS 是一种非常有用的图遍历算法，适用于多种场景。通过递归或迭代来实现 DFS，可以解决路径查找、连通分量检测等问题。理解 DFS 的基本原理和实现方法，是学习更复杂图算法的基础。

​

 在带权树网络中统计可连接服务器对数目[中等]

题目：

给你一棵无根带权树，树中总共有 n 个节点，分别表示 n 个服务器，服务器从 0 到 n - 1 编号。同时给你一个数组 edges ，其中 edges[i] = [ai, bi, weighti] 表示节点 ai 和 bi 之间有一条双向边，边的权值为 weighti 。再给你一个整数 signalSpeed 。

如果两个服务器 a ，b 和 c 满足以下条件，那么我们称服务器 a 和 b 是通过服务器 c 可连接的 ：

  • a < b ，a != c 且 b != c 。
  • 从 c 到 a 的距离是可以被 signalSpeed 整除的。
  • 从 c 到 b 的距离是可以被 signalSpeed 整除的。
  • 从 c 到 b 的路径与从 c 到 a 的路径没有任何公共边。

请你返回一个长度为 n 的整数数组 count ，其中 count[i] 表示通过服务器 i 可连接 的服务器对的 数目 。

示例 1：

​

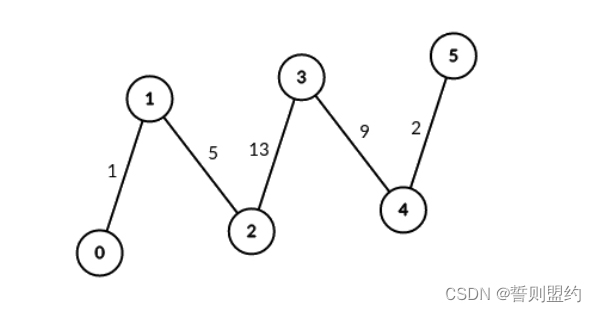
输入：edges = [[0,1,1],[1,2,5],[2,3,13],[3,4,9],[4,5,2]], signalSpeed = 1
输出：[0,4,6,6,4,0]
解释：由于 signalSpeed 等于 1 ，count[c] 等于所有从 c 开始且没有公共边的路径对数目。
在输入图中，count[c] 等于服务器 c 左边服务器数目乘以右边服务器数目。

示例 2：

​

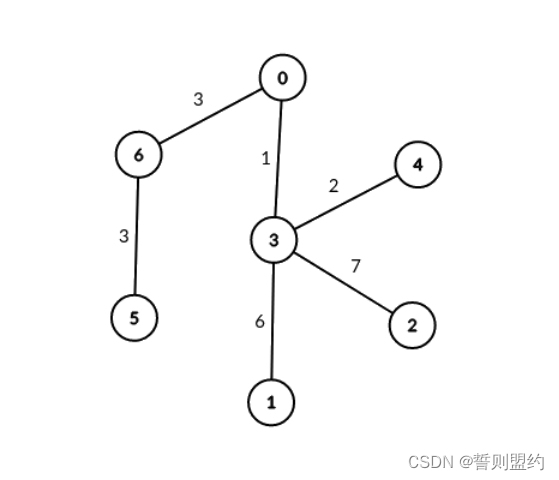
输入：edges = [[0,6,3],[6,5,3],[0,3,1],[3,2,7],[3,1,6],[3,4,2]], signalSpeed = 3
输出：[2,0,0,0,0,0,2]
解释：通过服务器 0 ，有 2 个可连接服务器对(4, 5) 和 (4, 6) 。
通过服务器 6 ，有 2 个可连接服务器对 (4, 5) 和 (0, 5) 。
所有服务器对都必须通过服务器 0 或 6 才可连接，所以其他服务器对应的可连接服务器对数目都为 0 。

提示：

  • 2 <= n <= 1000
  • edges.length == n - 1
  • edges[i].length == 3
  • 0 <= ai, bi < n
  • edges[i] = [ai, bi, weighti]
  • 1 <= weighti <= 106
  • 1 <= signalSpeed <= 106
  • 输入保证 edges 构成一棵合法的树。

题目分析：

        大致可以看出来这道题考察的是dfs+枚举 ，把每一个节点所连接的节点和权重加到一个列表里面储存，然后依次遍历这些节点，计算符合题意的解，加入到结果列表里面，返回结果即可。但是刚开始没有思路，不知从何下手，访问了题解区才完成代码实现。 

代码实现：

class Solution:
    def countPairsOfConnectableServers(self, edges: List[List[int]], signalSpeed: int) -> List[int]:
        def dfs(a: int, fa: int, ws: int) -> int:
            cnt = 0 if ws % signalSpeed else 1
            for b, w in g[a]:
                if b != fa:
                    cnt += dfs(b, a, ws + w)
            return cnt

        n = len(edges) + 1
        g = [[] for _ in range(n)]
        for a, b, w in edges:
            g[a].append((b, w))
            g[b].append((a, w))
        ans = [0] * n
        for a in range(n):
            s = 0
            for b, w in g[a]:
                t = dfs(b, a, w)
                ans[a] += s * t
                s += t
        return ans

总结：

        这段代码实现了一个计算可连接服务器对数的算法。具体来说，该算法通过深度优先搜索（DFS）计算树中每对连接的服务器节点之间可传输信号的数量。

        首先，在 countPairsOfConnectableServers 方法中，定义了一个内部的 DFS 函数 dfs，用来计算从节点 a 出发，传输信号速度为 ws 时，与相邻服务器节点的连接对数量。

        然后，初始化变量 n 为服务器节点数量加一，初始化空列表 g 用来存储图的邻接表。接着，将输入的边信息 edges 添加到邻接表 g 中。

        继续，初始化长度为 n 的全零列表 ans 用来存储每个节点的连接对数。然后对每个节点 a 进行遍历，计算与相邻节点 b 的连接对数量，并将结果存储在 ans 中。

        最后，返回 ans，即每个节点的连接对数的列表。

​

【版权声明】本文为华为云社区用户原创内容，转载时必须标注文章的来源（华为云社区）、文章链接、文章作者等基本信息， 否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
数据结构 网络
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入