@[toc]

前言

除了去年11月份以及今年近几月的算法刷题之外，只有在当时20年蓝桥杯准备的时候才刷过一些题，在当时就有接触到一些动归、递归回溯、贪心等等，不过那会也还是一知半解，做的题目也特别少，因为考虑到之后面试有算法题以及数据结构算法对于一个程序员十分重要，我也开始了刷题之路。

我目前的学习数据结构与算法及刷题路径：

1、学习数据结构的原理以及一些常见算法。

2、代码随想录：跟着这个github算法刷题项目进行分类刷，在刷题前可以学习一下对应类别的知识点，而且这里面每道题都讲的很详细。

3、牛客网高频面试101题：牛客网—面试必刷101题，在刷的过程中可以在leetcode同步刷一下。

4、接下来就是力扣上的专栏《剑指offer II》、《程序员面试金典（第 6 版）》…有对应的精选题单来对着刷即可。

5、大部分的高频面试、算法题刷完后，就可以指定力扣分类专栏进行一下刷题了。

刚开始刷的时候真的是很痛苦的，想到去年一道题可能就需要好几小时，真的就很难受的，不过熬过来一切都会好起来，随着题量的增多，很多题目你看到就会知道使用什么数据结构或者算法来去求解，并且思考对应的时间空间复杂度，并寻求最优解，我们一起加油！

我的刷题历程

截止2022.8.18：

1、牛客网101题(其中1题是平台案例有问题)：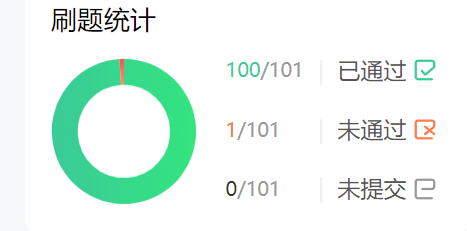

2、剑指offerII：

力扣总记录数：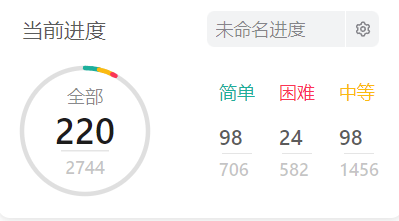

加油加油！

剑指offer

剑指 Offer 53 - II. 0～n-1中缺失的数字【简单】

题目链接：剑指 Offer 53 - II. 0～n-1中缺失的数字

题目内容：一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

思路：

1、遍历比对索引法

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

class Solution {
    //核心：递增、唯一
    //遍历一遍，若是索引与值不匹配那么就是缺失该值，否则返回长度
    public int missingNumber(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            if (i != nums[i]) {
                return i;
            }
        }
        return nums.length;
    }
}

2、二分排序法

class Solution {

    //二分法
    public int missingNumber(int[] nums) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            //只有两种情况mid与nums[mid]，一种就是>，另一种就是=
            if (mid == nums[mid]) {
                left = mid + 1;
            }else {
                right = mid - 1;
            }
        }
        return left;
    }
}

牛客

二分查找-I【简单】

题目地址：二分查找-I

题目描述：给定一个 元素升序的、无重复数字的整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标（下标从 0 开始），否则返回 -1。

思路1：设置左右结点，不断取中间值来进行二分查找。

复杂度分析：

• 时间复杂度：O(logn)
• 空间复杂度：O(1)·

import java.util.*;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param nums int整型一维数组 
     * @param target int整型 
     * @return int整型
     */
    public int search (int[] nums, int target) {
        if (nums.length == 0) {
            return -1;
        }
        int left = 0;
        int right = nums.length;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[mid] > target) {
                right = mid - 1;
            }else if (nums[mid] < target){
                left = mid + 1;
            }else{
                return mid;
            }
        }
        return -1;
    }
}

旋转数组的最小数字【简单】

题目地址：旋转数组的最小数字

题目描述：有一个长度为 n 的非降序数组，比如[1,2,3,4,5]，将它进行旋转，即把一个数组最开始的若干个元素搬到数组的末尾，变成一个旋转数组，比如变成了[3,4,5,1,2]，或者[4,5,1,2,3]这样的。请问，给定这样一个旋转数组，求数组中的最小值。

思路1：遍历一遍找到最小值

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

import java.util.*;
import java.util.ArrayList;
public class Solution {
    public int minNumberInRotateArray(int [] array) {
        int ans = array[0];
        for (int i = 1; i < array.length; i++) {
            if (array[i] < ans)
                ans = array[i];
        }
        return ans;
    }
}

思路2：二分排序法（推荐）

思路：由于旋转的数据都是升序到后面部分，那么依旧可以通过二分法来解决

复杂度分析：

• 时间复杂度：O(logn)
• 空间复杂度：O(1)

import java.util.*;
import java.util.ArrayList;
public class Solution {
    public int minNumberInRotateArray(int [] array) {
        int left = 0;
        int right = array.length - 1;
        while (left < right) {
            int mid = (left + right) / 2;
            if (array[mid] > array[right]) {
                left = mid + 1;
            }else if(array[mid] == array[right]) {
                right--;
            }else {
                right = mid;
            }
        }
        return array[left];
    }
}

二维数组中的查找【中等】

题目地址：二维数组中的查找

题目描述：在一个二维数组array中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

思路1：通过递归+剪枝来查找数组中得元素。

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

public class Solution {
    
    //判断是否找到
    private boolean flag = false;
    
    public boolean Find(int target, int [][] array) {
        //若是为空数组直接返回
        if (array.length == 1 && array[0].length == 0) {
            return flag;
        }
        //从左下角来进行出发
        isFind(array, array.length - 1, 0, target);
        return flag;
    }
    
    public void isFind(int [][] array, int i, int j, int target) {
        //越界条件
        if (i < 0 || (array.length > 0 && j == array[0].length))  {
            return;
        }
        //满足条件结束
        if (array[i][j] == target) {
            flag = true;
            return;
        }
        //剪枝
        if (!flag) {
            //递归
            //情况1：若是当前得值<目标值，那么向右移动一格
            if (array[i][j] < target) {
                isFind(array, i, j + 1, target);
            }else {
                //情况2：若是当前值>目标值，那么向上移动一格
                isFind(array, i - 1, j, target);
            }
        }
    }
}

同上得迭代遍历写法：

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        //边界条件
        if (matrix.length == 0 || (matrix.length == 1 && matrix[0].length == 0)) {
            return false;
        }
        int i = matrix.length - 1;
        int j = 0;
        //进行迭代遍历
        while (i >= 0 && j < matrix[0].length) {
            if (matrix[i][j] < target) {
                j++;
            }else if (matrix[i][j] > target) {
                i--;
            }else {
                return true;
            }
        }
        return false;
    }
}

寻找峰值【中等】

题目地址：寻找峰值

题目描述：给定一个长度为n的数组nums，请你找到峰值并返回其索引。数组可能包含多个峰值，在这种情况下，返回任何一个所在位置即可。

1.峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于
2.假设 nums[-1] = nums[n] = -\infty−∞
3.对于所有有效的 i 都有 nums[i] != nums[i + 1]
4.你可以使用O(logN)的时间复杂度实现此问题吗？

思路1：采用二分查找法

复杂度分析：

• 时间复杂度：O(logn)
• 空间复杂度：O(1)

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param nums int整型一维数组 
     * @return int整型
     */
    public int findPeakElement (int[] nums) {
        int left = 0;
        int right = nums.length - 1;
        while (left < right) {
            int mid = (left + right) / 2;
            if (nums[mid] > nums[mid + 1]) {
                right = mid;
            }else {
                left = mid + 1;
            }
        }
        return right;
    }
}

数组中的逆序对【中等】

题目地址：数组中的逆序对

题目描述：在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P mod 1000000007

• 重点：数组中得某个元素值>其后面得元素值。

思路1：暴力法（不推荐，超时）

public class Solution {
    public int InversePairs(int [] array) {
        int kMod = 1000000007;
        int res = 0;
        for (int i = 0; i < array.length; i++) {
            for (int j = i + 1; j < array.length; j++) {
                if (array[i] > array[j]) {
                    res++;
                    res = res % kMod;
                }
            }
        }
        return res;
        
    }
}

思路2：归并排序，过程中同样需要进行排序，细节的就是其中cnt = (cnt + mid - i + 1)，利用排序省去了多次的重复比较

复杂度分析：

• 时间复杂度：O(nlogn)
• 空间复杂度：O(1)

public class Solution {
    
    private int kMod = 1000000007;
    private int cnt;
    
    public void divide(int []arr, int start, int end) {
        //递归终止结束
        if (start >= end) {
            return;
        }
        int mid = (start + end) / 2;
        
        //递归分
        divide(arr, start, mid);
        divide(arr, mid + 1, end);
        
        //治
        merge(arr, start, mid, end);
    }
    
    public void merge(int[] array, int start, int mid, int end) {
        int k = 0;
        //创建一块一维数组空间
        int[] temp = new int[end - start + 1];
        //排序比对，过程中计算大于数量
        int i = start,j = mid + 1;
        while (i <= mid && j <= end) {
            if (array[i] <= array[j]) {
                temp[k++] = array[i++];
            }else {
                temp[k++] = array[j++];
                //核心：这里来进行统计对应区间>0的个数
                cnt = (cnt + mid - i + 1) % kMod;
            }
        }
        //处理剩下来的值
        while (i <= mid) {
            temp[k++] = array[i++];
        }
        while (j <= end) {
            temp[k++] = array[j++];
        }
        //覆盖原数组
        System.arraycopy(temp, 0, array, start, end - start + 1);
    }
    
    public int InversePairs(int [] array) {
        if (array == null || array.length <= 1) {
            return -1;
        }
        divide(array, 0, array.length - 1);
        return cnt;
    }
}

leetcode

4. 寻找两个正序数组的中位数【困难】

学习：详细通俗的思路分析，多解法

题目链接：4. 寻找两个正序数组的中位数

题目内容：给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

思路：

1、遍历寻找

复杂度分析：时间复杂度O(m+n)；空间复杂度O(1)

class Solution {

    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int a = nums1.length, b = nums2.length;
        int len = a + b;
        //设置起始点
        int aStart = 0, bStart = 0;
        int left = -1, right = -1;
        //遍历一半节点，并能够找到中位数
        for (int i = 0; i <= len / 2; i++) {
            left = right;
            //根据条件来取对应数组中的元素
            if (aStart < a && (bStart >= b || nums1[aStart] < nums2[bStart])) {
                right = nums1[aStart++];
            }else {
                right = nums2[bStart++];
            }
        }
        //判断记录总数是否为偶数
        if ((len & 1) == 0) {
            return (left + right) / 2.0; 
        }else {
            return right;
        }
    }
}

2、二分查找。可以将时间复杂度优化为O(logn(n+m))

示例：

我也是先看别人的示例，然后去取了几个例子走了一遍，然后跟着之前推算案例的例子来进行实现。

class Solution {

    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int a = nums1.length;
        int b = nums2.length;
        int len = a + b;
        //取得指定中间位置值
        int k1 = (len + 1) / 2;
        int k2 = (len + 2) / 2;
        if (k1 == k2) {
            return findK(nums1, 0, a - 1, nums2, 0, b - 1, k1);
        }
        return (findK(nums1, 0, a - 1, nums2, 0, b - 1, k1) + findK(nums1, 0, a - 1, nums2, 0, b - 1, k2)) / 2.0;
    }


    public double findK(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) {
        //计算两个长度
        int len1 = end1 - start1 + 1;
        int len2 = end2 - start2 + 1;
        //始终让nums1为长度最小的
        if (len1 > len2) return findK(nums2, start2, end2, nums1, start1, end1, k);
        //若是nums1的长度为0，此时直接返回对应nums2的下标
        if (len1 == 0) return nums2[start2 + k - 1];
        //若是目标数量为1，那么返回相对较小的一个值
        if (k == 1) return Math.min(nums1[start1], nums2[start2]);
        //开始来进行缩减范围
        //首先确定要比较的位置（确保不会越界）
        int i = start1 + Math.min(len1, k / 2) - 1;
        int j = start2 + Math.min(len2, k / 2) - 1;
        if (nums1[i] > nums2[j]) {
            //缩减nums2的范围
            return findK(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));
        }else {
            return findK(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));
        }
    }
}