【每日一读】Research on power-law distribution of long-tail data and i
@TOC

简介
Hello!
非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~
ଘ(੭ˊᵕˋ)੭
昵称:海轰
标签:程序猿|C++选手|学生
简介:因C语言结识编程,随后转入计算机专业,获得过国家奖学金,有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验:扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语!
唯有努力💪
本文仅记录自己感兴趣的内容
Abstract
目的 – 旅游推荐系统 (TRS) 面临的一个挑战是旅游产品中评级或受欢迎程度的长尾现象。本文旨在利用长尾数据的幂律分布来提高TRS的多样性和效率。
设计/方法/方法——以新浪微博签到数据为例,证明长尾现象存在于用户出行行为,并以幂律分布拟合长尾出行数据。为解决长尾部分数据稀疏问题,增加TRS的推荐多样性,提出一种结合幂律分布的协同过滤(CF)推荐算法。此外,将幂律分布与局部敏感哈希(LSH)相结合,对用户相似度计算进行优化,以提高TRS的计算效率。
结果——对比实验表明,该算法在保持推荐的高精度和召回率,为进一步的动态推荐提供依据。
原创性/价值——TRS 为旅游领域的信息过载问题提供了更好的解决方案。然而,基于全人群的历史旅行数据,目前的TRS大多倾向于向用户推荐热点和相似的景点,缺乏多样性,无法提供个性化的推荐。同时,在线社交网络(OSN)中的大量高维稀疏数据在使用传统CF算法计算用户相似度时带来了巨大的计算成本。本文通过将旅游数据的幂律分布与旅游推荐技术相结合,解决了传统TRS中存在的推荐结果过于狭窄、缺乏偶然性的问题,为用户提供了更广泛的选择余地。从而改善 TRS 中的用户体验。同时,利用局部敏感哈希函数,作者的工作将用户从高维向量哈希到一维整数,并将相似用户映射到相同的桶中,实现了在高维空间中的快速最近邻搜索,解决了极端稀疏问题高维旅行数据。此外,将哈希结果应用于用户相似度计算,大大降低了计算复杂度,提高了TRSs的计算效率,降低了系统负载,使TRSs能够为用户提供有效及时的推荐。
1. Introduction
近年来,经济的增长和居民消费水平的提高,拉动了对旅游的需求,带动了旅游业的快速发展。同时,随着互联网技术的发展,用户可以更容易地通过移动应用程序和社交媒体获取旅游服务信息,例如:旅游目的地特色景点、餐厅、酒店等,其活动带来海量在线旅游数据。在这种情况下,越来越多的人更愿意选择“无计划的旅行”。他们可能没有足够的时间和精力在旅行前和旅行期间对目的地的景点、餐厅和酒店进行彻底调查,他们的决策面临信息过载的问题。因此,如何从海量信息中快速准确地发现用户的出行偏好,成为在线用户和商家共同面临的挑战。
推荐系统(RS)是解决信息过载问题的典型技术(Chang et al., 2017)。与一般RSs相比,个性化旅游推荐系统(TRSs)旨在发现与用户旅游偏好完全匹配的旅游产品或服务,可以帮助旅行者从海量数据中快速挑选出合适的旅游产品。然而,随着对TRS研究的深入和成熟,学者们发现,传统的以准确性为导向的TRS可能会从以下两个角度导致推荐缺乏多样性,无法满足用户需求。首先,从用户的角度来看,以准确性为导向的 TRS 可能缺乏推荐的偶然性并导致用户不满意。以准确性为导向的 TRS 容易向用户推荐相似或热门的目的地和景点,而这些目的地和景点很可能已被其他来源的用户所知,远不能达到真正的个性化推荐,也不太可能帮助旅行者规划出满足自己需求的合适的旅行路线和兴趣(Chiang 和 Huang,2015 年)。其次,从在线商家的角度来看,以准确性为导向的 TRS 往往会生成过于狭窄的推荐集,也可能使商家不满意。只注重准确性的 TRS 无法推荐小众或冷启动商品,而这些商品可能具有较高的商业价值和吸引用户购买的潜力。结果,在线商家可能会失去利基目的地或服务带来的利润,因为它们很难被推送给用户。因此,如何提高推荐结果的多样性成为TRSs中的一个关键问题。
为了解决TRSs中的多样性问题,目前的研究从以下几个方面对旅游推荐算法进行了改进。对于协同过滤(CF)推荐,结合概率统计和人工智能算法,根据用户旅行记录、用户相似性和用户位置关系预测用户可能的偏好景点(Cui et al., 2018; Gasparetti, 2017)。鉴于异构集体智能,更好的相似性度量可以通过融合用户交互和不同用户上传的多模态旅行信息来进一步提高 CF 算法的性能(Shen 等,2016)。对于基于内容的推荐,使用社交媒体中的文本标签和地理标签照片来检测和扩展目的地属性,并利用用户之间的社交关系来挖掘用户的旅行偏好(Shen et al., 2016; Zhou et al., 2018;Memon 等人,2015;Cai 等人,2018)。虽然在一定程度上增加了推荐的多样性,但上述研究只是从算法的角度进行了改进。他们中很少有人考虑旅行数据的特性。最近,其他相关研究开始关注用户数据的特征,并在用户健忘、新颖性要求(Kapoor et al., 2015)、偏好转换(Chou et al., 2016)等方面定性地解释了用户数据的多样性。 、用户期望 (Adamopoulos 和 Tuzhilin, 2014)、项目未来流行度 (Abbas et al., 2018) 和用户评分模式 (Lathia et al., 2010)。但他们很少考虑用户数据的整体特征,也没有很好地将数据特征融入推荐技术中。因此,主要研究问题和贡献之一是从用户旅行数据特征的角度提高TRS的推荐多样性。
此外,用户旅游行为具有以下特点:旅游目的地的高度多样性和同一目的地的频率低,导致旅游数据的维度极高,对旅游推荐提出了新的挑战。此外,随着TRS中用户和资源的激增,数据规模呈几何级增长。在这种情况下,数据的高维和稀疏问题更加突出,对推荐算法的时效性和性能造成了越来越大的压力。
为了解决TRS中的这个问题,学者们提出了各种技术,包括主成分分析(PCA)、正则矩阵分解(RMF)、奇异值分解(SVD)、随机游走等(Berjani和Strufe,2011;Yinget)等人,2014)。然而,此类技术对于超大规模、高维的旅行数据效果不佳,扩展性差,离线计算负担重。解决这个问题的另一种方法是使用索引结构在高维数据中搜索最近邻,并根据最近邻的出行行为进行推荐。但是由于当数据的维数超过一定阈值时,索引方法的性能会下降到线性扫描的性能(Weber et al., 1998),旅行数据的高维可能会导致索引方法的失败或性能下降,并且导致算法复杂度增加,搜索效率下降。因此,本文的另一个研究问题和贡献是分析出行数据的分布特征,利用数据分布特征避免数据高维导致的性能下降。
受上述问题的启发,在本文中,我们尝试利用旅行数据和局部敏感哈希(LSH)的特征来提高TRS的推荐多样性和计算效率,这是一种用于近似最近邻搜索的有效索引结构(Liu et al., 2014a) ,b;拉奇科夫斯基,2018 年)。首先,我们探索了旅行数据的分布,并在 TRS 中应用分布特征来增加推荐的多样性。在旅游领域,用户在移动应用中提交的信息相对单一和不变,不同旅游目的地的评分或热度表现出很大的异质性。也就是说,大多数评分/评论只集中在少数热门项目上,称为长尾现象(Hu et al., 2017)。
在本文中,我们使用ONS中的签到数据分析了旅行数据的长尾现象,并验证了长尾旅行数据的幂律分布。通过长尾旅行数据的幂律分布与推荐技术的深入结合,更多的新目的地或新内容进入推荐列表,增加了推荐的多样性,为基于整体的推荐算法改进提供了一种思路。大数据的特点。其次,我们尝试将 LSH 引入相似度计算中,以提高 TRS 的计算效率。使用局部敏感哈希函数,我们将用户从高维向量哈希到低维二进制整数,并将具有相似旅行偏好的用户映射到相同的桶。在此基础上,我们只计算同一桶内用户的相似度,并根据同一桶内用户的出行偏好进行推荐,为快速最近邻搜索和高维出行数据的极端稀疏问题提供了可行的解决方案。实验结果表明,我们提出的算法在推荐长尾旅游目的地和预测用户位置方面表现良好。
2. Literature review
文献综述主要关注以下三个方面:旅游推荐系统、幂律分布、局部敏感散列。
2.1 Tourism recommendation systems (TRSs)
2.2 Power-law distribution
现有研究指出,用户对商品的评分存在长尾现象,这意味着大多数评分/评论仅集中在少数热门商品中(Hu et al., 2017)。
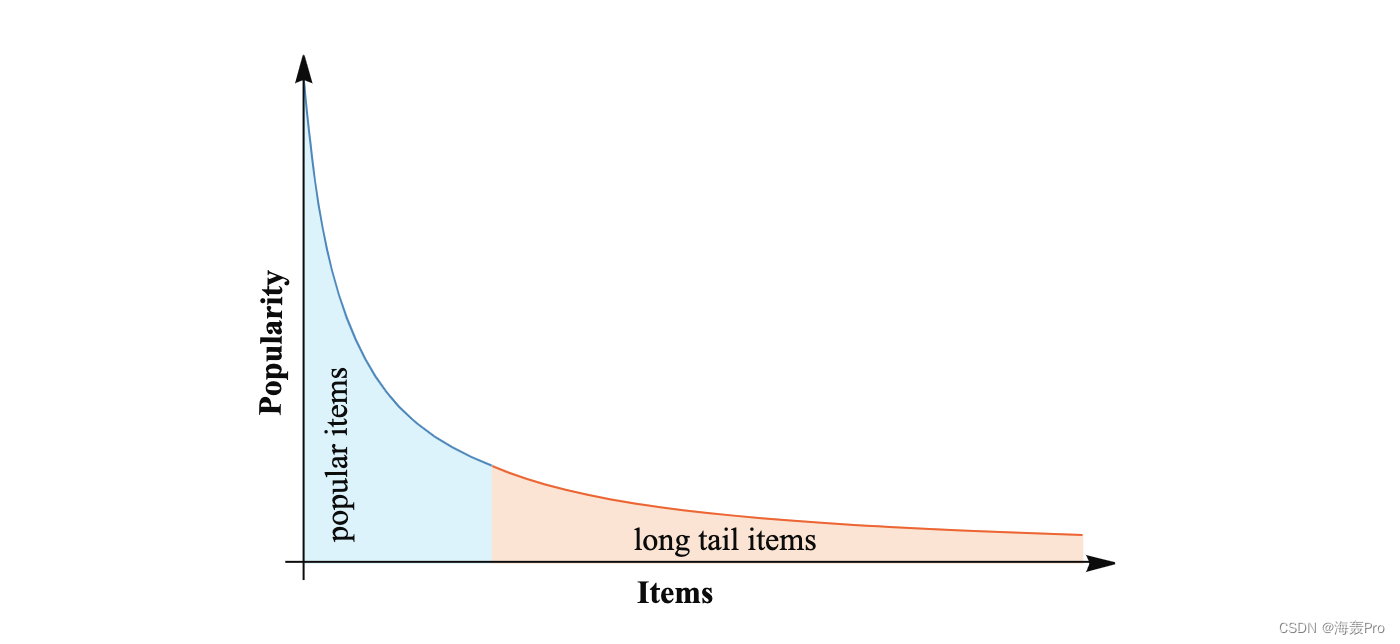
图 1 展示了物品之间受欢迎程度的长尾分布,其中纵轴代表评论、评分、访问等方面的物品受欢迎程度,横轴代表物品受欢迎程度的排名。
如图 1 所示,左侧的项目(蓝色区域)被称为热门项目,因为它们收到更多的评分、评论或访问。而右侧(黄色区域)则被认为是冷门或新品,称为长尾品。长尾问题是指由于长尾项目的极端数据稀疏性,导致热度较高的产品或地点更容易被推荐,导致马太效应和推荐结果的低多样性。然而,类似的结果可能会让用户感到厌烦,一个好的推荐系统应该为用户提供多样化的选择。因此,如何有效利用长尾数据给出多样化和个性化的推荐成为了TRSs一个有价值的研究方向。
在这种情况下,学者们开始关注TRSs中的长尾现象,并发展了一些长尾推荐算法。朱等。表明 TRS 面临的三个挑战是旅游产品的高内容复杂性、用户-项目矩阵的极度稀疏性和冷启动用户的普遍存在。他们将上述问题转化为长尾项目的推荐,并提出了一种基于主题序列模式的旅游产品推荐算法来解决这些问题(Zhu et al., 2017)。 Park 和 Chu 通过在推荐之前对长尾部分的项目进行聚类来改进推荐算法(Park 和 Chu,2009)。殷等。通过用无向边加权图表示用户项目信息,提出了一套基于图的长尾推荐算法(Yin 等人,2012)。Adamopoulos 和 Tuzhulin 使用意外推荐的概念来命名 RS,旨在推荐不受欢迎或意外的项目,并提出了几种基于效用理论或概率方法生成此类推荐的算法(Adamopoulos,2013;Adamopoulos 和 Tuzhilin,2011,2014)。王等人。设计一个同时考虑推荐准确性和多样性的多目标函数,并提出一种进化推荐算法,通过优化多目标函数来找到权衡解决方案(Wang et al., 2016)。胡等。讨论长尾推荐存在的问题,并提出一些措施(如长尾稳定性、深度、层次等)作为长尾推荐的评价标准(Hu et al., 2017)。虽然在旅游产品长尾推荐方面已经有了初步的探索,但目前的研究很少对长尾旅游数据的分布特征进行深入分析,更谈不上在长尾推荐中的应用。
幂律分布是一种典型的长尾分布,在自然科学和社会科学中普遍存在,包括物理学、生物学、地球科学、天体物理学、经济学、计算机科学和人口统计学。 Pareto 和 Zipf 是两位公认的先驱,他们对幂律做出了巨大贡献。帕累托原则(也称为 80/20 规则)指出,大约 80% 的资源由 20% 的人口拥有,齐夫定律表明任何单词的频率与其在自然语言语料库中的排名成反比.然后,其他学者发现幂律存在于许多领域,包括城市规模分布、地震烈度、福利强度、论文引用和页面浏览量等(Clauset et al., 2009)。此外,作为唯一的无标度分布,幂律分布被视为复杂网络的基本性质之一(Albert 和 Barabasi,1999;Girvan 和 Newman,2002)。
值得一提的是,OSN 中的用户行为也被证明是无标度的(Jeonget al., 2000)。在过去的几年里,数十亿人加入了 OSN,他们的活动在社交网络应用程序上产生了大量的用户数据。因此,关于基于 OSN 中用户数据的个性化推荐的研究越来越多(Jafarpour 和 Kardan,2015;Samanthula 和江,2015)。大量研究表明,用户行为中存在一些稳定的特征或规律,幂律是其中重要的一个(Mislove et al., 2007; Fu et al., 2007; Yuta et al., 2007)。吴等人。指出幂律分布作为社交网络的重要属性,在社区检测、兴趣挖掘、行为模式挖掘和社会搜索等方面具有重要的应用价值(Wu et al., 2014)。然而,目前的研究主要集中在分析社交网络的幂律分布和用户行为,很少涉及其应用。
从 TRS 的角度来看,幂律分布可以分为两部分:头部和长尾。头部代表少数以非常高的频率出现的热门项目,随后的长尾代表以低频率出现的大多数项目。尽管热门项目反映了大多数用户的兴趣和偏好,但它们无法帮助进行个性化推荐,因为热门项目通常为所有用户所熟知。因此,一个更符合用户需求的推荐算法应该包括长尾项目,并为用户提供更多样化的推荐结果。在此背景下,如何挖掘 TRS 中幂律性质的潜在价值,如如何将幂律性质纳入推荐算法,解决长尾数据稀疏和冷启动问题,是一个有价值的研究课题。推荐,如何有效利用头部数据和长尾数据提供多样化和个性化的推荐。
2.3 Locality sensitive hashing
TRS处理的数据集通常是海量的、高维的,在离线计算上带来巨大的计算成本。因此,如何通过降维来提高计算效率一直是TRSs的一个重要研究方向。用户最近邻模型是解决此问题的成功 CF 技术之一(Yang 等人,2012)。作为高维空间中一种有效的最近邻搜索方法,LSH 可以更好地克服 k-最近邻(KNN)搜索中的维数灾难,受到学者们的广泛关注(Indykp 和 Motwani,1998;Slaney 和 Casey,2008)。它被证明具有比线性复杂度更低的计算复杂度,广泛应用于图像检索、音频检索、文本检索等领域。传统的KNN算法本质上是一个top-K问题。其复杂度通常大于OðdnÞ,而LSH的复杂度较低,为Oðdn1=εÞ,其中n是数据点的个数,d是数据点的维数,ε是LSH的参数。
最近,哈希学习方法已被应用于提高 RS 的计算效率。哈希学习方法的基本思想是将用户评分矩阵作为用户和物品之间的相似度矩阵。基于用户-项目相似度矩阵,它使用散列函数学习用户和项目的低维二进制代码。然后计算二元空间中用户和物品之间的汉明距离,其中用户和物品之间的距离越小意味着它们之间的相似度越高,表明用户对物品的兴趣越高。周等人。提出了一种学习协同过滤二进制代码(BCCF)的方法,它将学习过程分为两个独立的阶段:实值优化和二进制代码量化(Zhou et al., 2018)。在实值优化阶段,通过放宽二元约束和矩阵分解得到近似实值解。在二进制码量化阶段,通过最小化实值和二进制码之间的损失函数得到用户和物品的二进制码。刘等人。为矩阵形式的数据提出了一种协作散列方案,同时保留不同视图中的实体相似性和视图之间的相互关系(Liu et al., 2014a, b)。他们证明了协作散列在保留用户偏好方面优于 BCCF。张等人。提出了一种偏好保留哈希(PPH)方法来加速推荐,该方法强调用户对项目的偏好而不是它们的相似性(Zhang et al., 2014)。他们指出哈希码只保留数据相似性而不是偏好,并为矩阵分解提出了一种新颖的常数特征约束,以确保用户的偏好与其相似性等价。
与其他散列学习方法相比,LSH 的优点是一旦给定散列函数就不受距离度量的限制。最近的研究进一步将 LSH 应用于 CF 建议并取得了显着的成功(Liu et al., 2014a, b; Liu and Wu, 2016)。但是,基于 LSH 的推荐存在一些问题。首先,散列学习侧重于保持数据相似性,而 RS 侧重于用户对项目的偏好。如上所述,用户偏好和相似度之间存在差异。其次,当用于最近邻搜索时,由于高维数据极度稀疏,LSH搜索到的最近邻和最远邻通常与高维空间中的用户的距离几乎相同,导致最近邻搜索或索引失败搜索。因此,很少有研究将 LSH 或哈希学习应用于地理定位或旅游推荐,而其他传统的降维方法已广泛应用于地理定位推荐的研究和实践,例如PCA、RMF、SVD 等。为了填补这一空白,我们需要根据旅行数据的特点,将LSH应用于高维旅行数据中的快速最近邻搜索。
综上所述,TRSs存在两个问题:推荐结果多样性低和出行数据维度高。同时,旅行数据和LSH的分布特征在TRSs中还没有得到很好的研究和重视。因此,在本文中,我们尝试将长尾旅行数据的幂律分布与LSH相结合,以提高TRSs的推荐多样性和计算效率。我们首先分析了基于新浪微博签到数据的出行数据的幂律特性,验证了用户签到频率和位置出现频率均服从幂律分布。然后,我们根据用户签到频率的幂律分布下界将所有用户分为活跃用户和非活跃用户。最后,我们使用 LSH 将数据点散列到桶中,通过计算每个桶中的用户相似度进行推荐,余弦相似度通过位置出现频率的幂律分布改进,这提供了更好的方法来避免维数灾难并提高长尾推荐的多样性。
3. The proposed HashCF algorithm
3.1 Power law of travel data—using Sina Weibo check-in data for example
对于互联网,幂律有着非常特殊的意义。许多核心现象都与幂律有着密切的联系,例如OSN的度分布、网页的连通性、用户上网行为等。大量研究表明,许多数据集的分布具有长尾,可以用幂律曲线拟合。随着智能手机的普及,基于位置的社交网络已经成为用户位置的重要数据来源,开始受到学者们的更多关注。在线旅游数据具有典型的幂律特征。也就是说,很少有热点出现频率高,大多数冷门出现频率很低。而在 TRS 中,只有少数热点经常被推荐,而大多数冷门很少被推荐。因此,幂律出现在旅行数据的特征和TRSs的结果中。
针对这一现象,本文以新浪微博签到数据为例,验证了出行数据的幂律分布,并进一步从理论上展示了如何利用它来提高推荐多样性。签到数据使用基于Java的开源网络爬虫WebCollector从新浪微博爬取。它包含来自 716 个用户的 1,994,559 条签到记录。爬取的字段包括用户ID、文本信息、签到地点、签到时间、签到设备,以及每条签到记录的支持数、重发数、评论数。表 I 报告了签入数据的一些样本。
在本节中,我们首先对地点的受欢迎程度进行描述性统计分析。
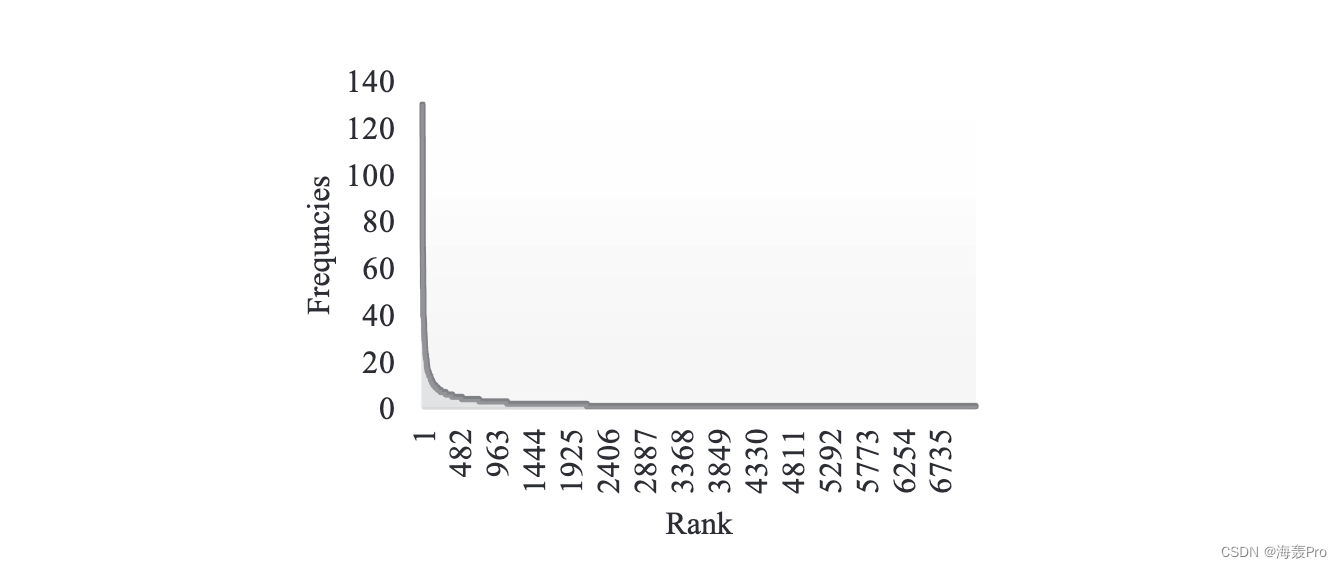
图 2 显示了签到位置的秩频散点图,
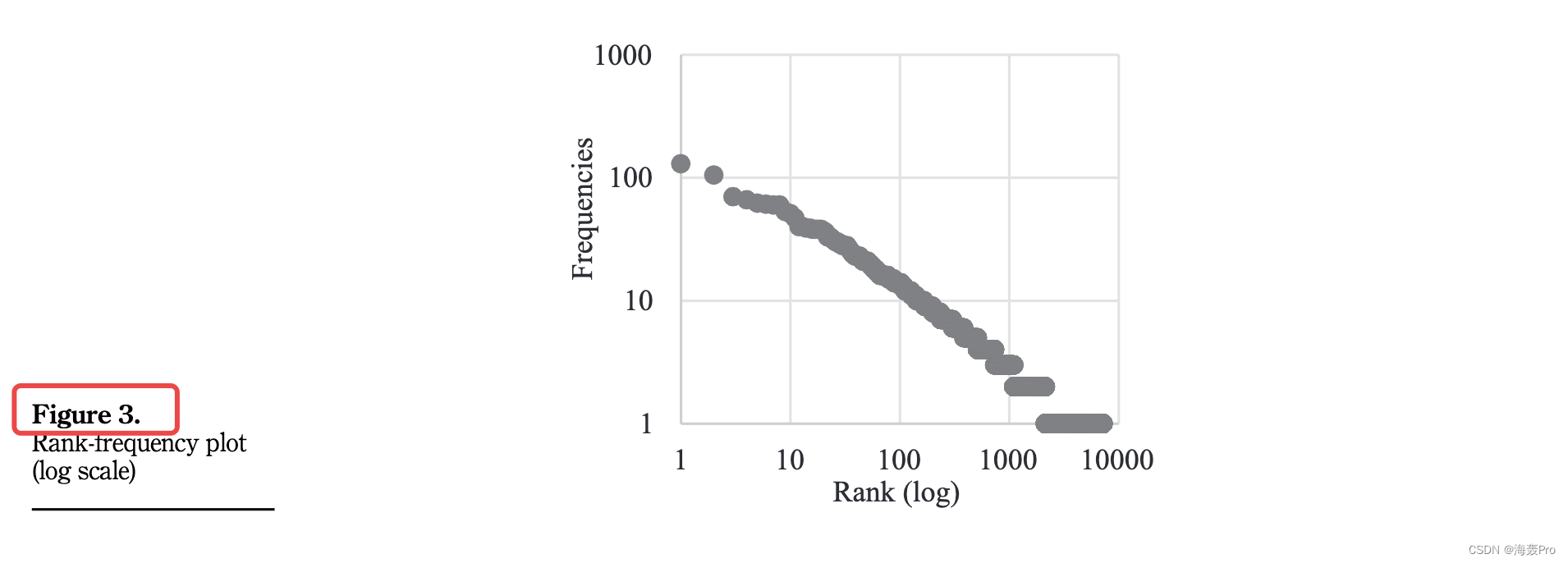
图 3 是其在双对数轴上的散点图。在图2中,纵轴代表位置流行度,以所有用户在某个位置的总签到次数表示,横轴代表位置流行度的排名。如图 2 和图 3 所示,签到位置的秩频率分布具有长尾,并且在双对数轴上近似线性分布,这意味着位置出现频率遵循近似幂律分布。
然后,在3.1.1和3.1.2节中,参考Clauset对幂律分布的研究(Clauset et al., 2009),我们对用户签到频率的幂律分布尺度参数进行了估计,以检验用户签到行为是否具有幂律性质。在 3.1.3 节,我们进一步估计幂律分布的下界,找出长尾分布的起点,为用户分类提供依据。
3.1.1 Estimation of scaling parameter
用户签到频率的分布可以定义为典型的幂律分布形式:
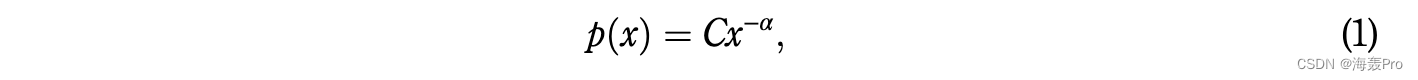
其中 C 是归一化常数,α 是幂律分布的标度参数。
在估计缩放参数 α 时,常用的方法是最小二乘线性回归。即,对等式两边取对数。 (1),幂律分布服从 lnpðxÞ 1/4 −αlnx−α þ lnC,在双对数轴上服从线性分布。可以通过执行普通最小二乘 (OLS) 回归来提取斜率 α。然而,Clauset 等人。表明 OLS 可能会产生 α 的有偏估计,因为对于大多数真实数据集,通常不满足 OLS 假设,例如归一化 (Clauset et al., 2009)。为了获得 α 的无偏估计,他们使用最大似然法估计 αvalue,并推导出离散情况的最大似然估计量 (MLE) bα。给定包含 N 个观测值的数据集 xi ≥ xmin;我 1/4 1; 2. . . ; N,MLE bα 是
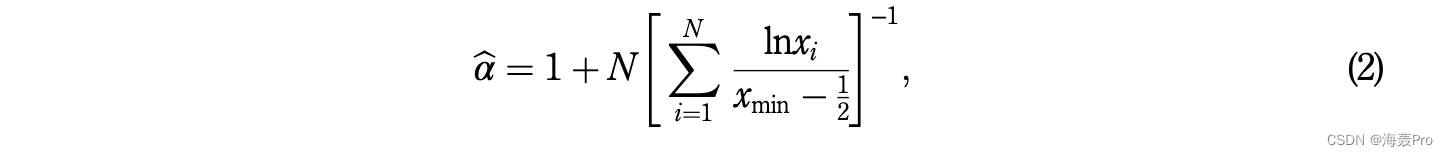
并且常数 C 可以使用 pðxÞ 在 x 的所有可能值上的总和为 1 的属性导出,即
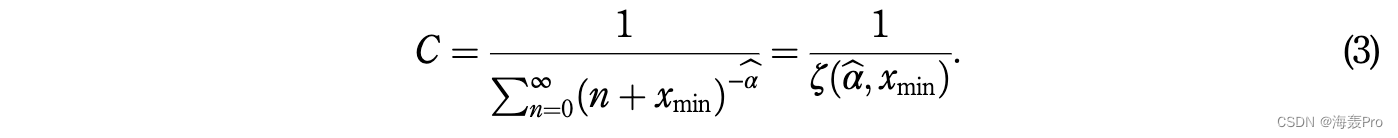
使用方程式。 (2) 和 (3),α 和 C 分别估计为 1.216284 和 0.216284。
3.1.2 Performance of scaling parameter estimators.
在实际情况下,我们通常不知道我们的数据是否是幂律分布的。在这种情况下,幂律分布的 MLE 仅告诉我们最适合幂律形式的模型,而不是幂律是否是适合数据的良好模型。因此,需要进行进一步的测试来评估 MLE 的性能。
MLE 仅保证在大样本量 N → ∞ 的渐近极限内无偏。克劳塞特等人。表明 N ≥ 50 是提取可靠参数估计值的合理经验法则。原因是对于非常小的数据集,即使数据不是真正的幂律分布,幂律分布也可能看起来很合适,因为 MLE 对此类数据的偏差远小于估计器的统计误差因此更容易被忽略。 bα 上的标准误差 σ 为
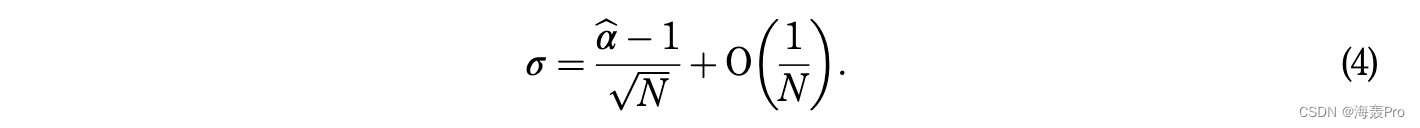
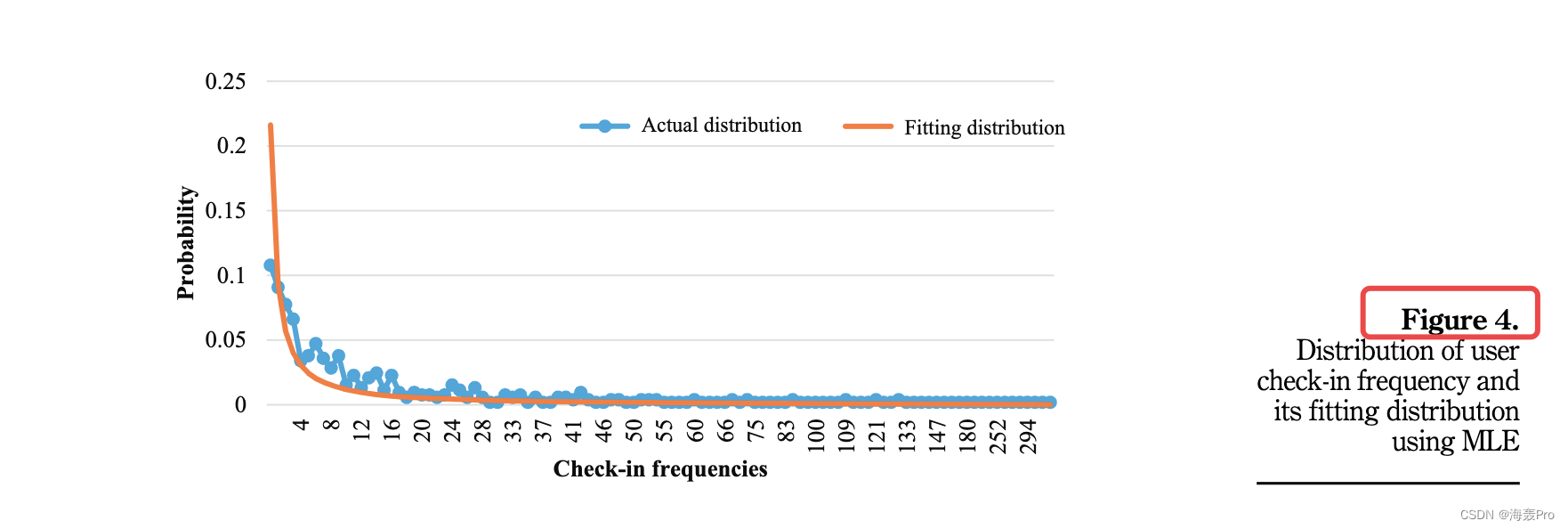
使用等式计算的 σ 估计值。 (4) 为 0.021。使用 SPSS 进行的拟合优度检验表明拟合优度为 0.920423,显着性值接近于零,表明幂律分布对用户签到数据的拟合度很好。图 4 给出了基于 MLE 估计参数的用户签到频率的实际分布及其拟合分布。
从图中可以看出,用户签到频率的分布是一条长尾分布,服从幂律分布。
3.1.3 Estimation of the lower bound on power-law behavior
在图 4 中可以看到数据在分布开始部分与拟合幂律分布的明显偏差,这告诉我们幂律分布仅适用于高于某个下限 xmin 的 x 值。
在估计缩放参数之前,我们需要丢弃所有低于 xmin 的样本,以确定幂律模型对剩余样本有效。因此,准确估计 xmin 的方法对于进一步估计 α 至关重要。对于太低的 xmin 值,由于我们试图将幂律模型拟合到非幂律数据,因此会获得缩放的有偏估计。另一方面,对于太高的 xmin 值,合法的幂律数据点被丢弃,导致缩放参数的统计误差和有限尺寸效应的偏差都增加。下界的估计是试图在上述两种情况之间找到一个很好的折衷值。
选择 bxmin 的传统方法是在对数对数图上直观地观察分布的概率密度函数 (PDF) 或累积分布函数 (CDF) 变得大致直线的起点,或者确定超出该起点的起点。作为 bxmin 函数的 bα 曲线变得相对稳定。但这些方法过于主观,对分布尾部的噪声或波动敏感。更客观和合适的方法是 Kolmogorov-Smirnov (KS) 方法,其基本思想是找到 bxmin 的最佳值,以最小化实际数据分布与其在区域 x ≥ 的最佳拟合幂律分布之间的距离最小。对于非正态数据,量化两个概率分布之间距离的最常用度量是 KS 统计量,定义为
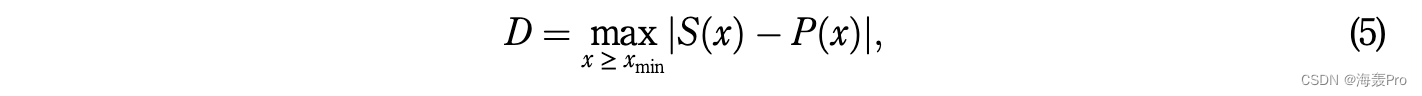
其中 SðxÞ 是值高于 bxmin 的观测数据的互补 CDF,PðxÞ 是最适合区域 x ≥ bxmin 的数据的幂律分布的互补 CDF。幂律分布下界 bxmin 的估计值是使 D 最小化的 xmin 的值。
在计算 D 值时,首先需要根据观测数据计算 SðxÞ,并根据 3.1.1 节中的方法得到的最佳拟合幂律分布推导出 PðxÞ。图 5 列出了当 xmin 范围为 1 到 10 时 D 的值。
我们可以看到,在点 xmin 1/4 3 处达到了 D 的最小值,这表明使用 KS 方法估计幂律分布的下限为 3。因此,我们在根据新浪微博签到数据进行推荐时,应该以3次签到作为用户分类的标准。即签到少于3次的用户属于非活跃用户,其他用户属于活跃用户。
3.2 Similarity calculation with LSH
LSH 是一种从海量数据中快速搜索相似项目的算法技术。 LSH 背后的一般思想近似于空间域变换和分区。使用不同的哈希函数,可以将高维坐标空间中的数据点映射为离散值,例如整数。局部敏感哈希函数是专门设计的,使得彼此靠近的数据点具有相同的哈希值的概率很高,而彼此远离的数据点可能具有不同的哈希值。这使得相似物品在经过 LSH 函数散列后保持相似度成为可能,这对于基于海量数据的 CF 推荐中的相似度计算和实现动态 CF 推荐具有很大的优势。
如今,如何基于海量高维数据快速计算用户/物品相似度已经成为影响TRSs效率和动态推荐实现的关键因素。 LSH 通过将高维空间中的数据点投影到低维空间中的哈希值,同时保持它们的相似性,为维度灾难提供了一种有效的解决方案,它还通过创建足够数量的哈希来帮助解决数据稀疏和冷启动问题具有不同哈希函数的表。
对于向量形式的数据,常用的相似度度量包括欧几里得距离、曼哈顿距离、杰卡德距离、汉明距离和余弦相似度等。本文采用余弦相似度来计算用户相似度。 Charikar 使用随机超平面舍入技术推导出余弦相似度的相似性保持散列函数,并证明基于随机超平面的散列函数是 d1; d2; ð180 - d1Þ=180; ð180 − d2Þ=180Þ 敏感(Charikar,2002)。因此,基于随机超平面的散列函数可用于散列用户签到向量数据。
新浪微博中的用户签到行为具有幂律分布特征。相应地,用户位置评分矩阵是高维且极其稀疏的。对于基于此类数据的推荐,LSH被认为是提高推荐性能的好方法。以下段落详细描述了使用基于随机超平面的 LSH 对用户签到数据进行哈希处理的过程。
首先,我们根据用户签到的历史数据构建用户位置矩阵。每个用户的签到记录可以表示为一个n维向量,u i! 1/4 fl1; l2; . . . ;磅;其中 n 是唯一位置的总数。
其次,假设两个用户之间的相似度可以通过余弦相似度来衡量,对于任何非零向量x! 1/4 效果器; x2; . . . ; xng在n维空间中,哈希函数定义为
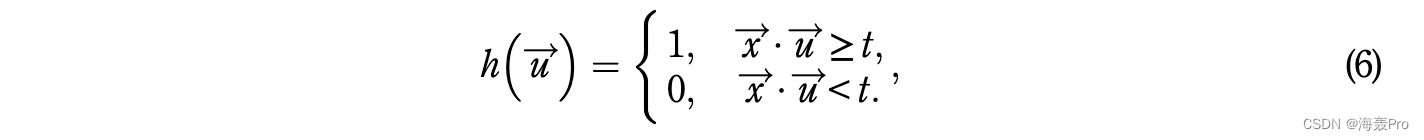
然后,通过随机选择 m 个非零 u!,我们得到 m 个哈希函数。每个向量都可以看作是一个超平面的法向量,原始数据空间可以被这m个散列函数分成若干个单元格。我们认为,如果两个用户经过哈希处理后位于同一个单元格中,则他们在原始数据空间中更可能相似(即他们之间的余弦相似度在原始数据空间中较高)。对于本文使用的用户签到数据,两个用户向量之间的夹角范围为[0, 90]。随机选择的非零向量应该尽可能均匀地划分数据空间。请注意,选择一个随机超平面可能需要大量的随机位。对于 n 维向量,可以通过选择 Oðlog 2nÞ 随机位来选择散列函数,从而将随机超平面限制在大小为 2Oðlog 2nÞ 的族中(Charikar,2002)。
最后,根据上述哈希函数得到的哈希表,我们将用户哈希到若干个桶中,并根据同一个桶中的用户进行KNN推荐。
3.3 HashCF algorithm considering power-law distribution
4. Results analysis
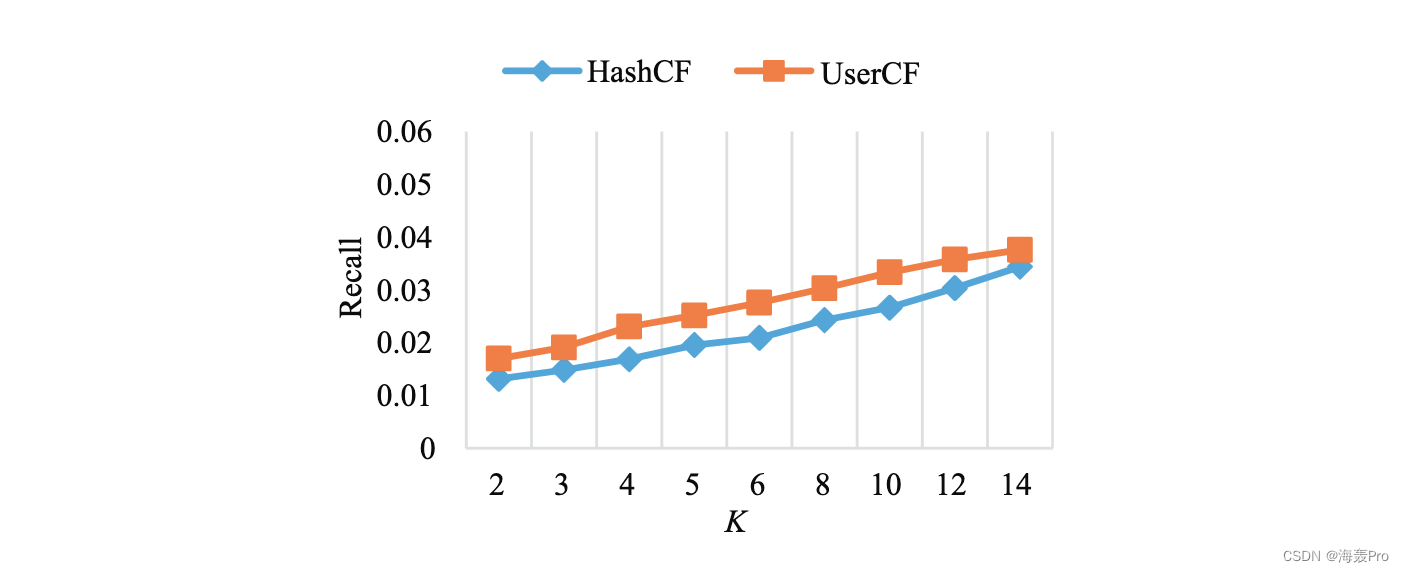
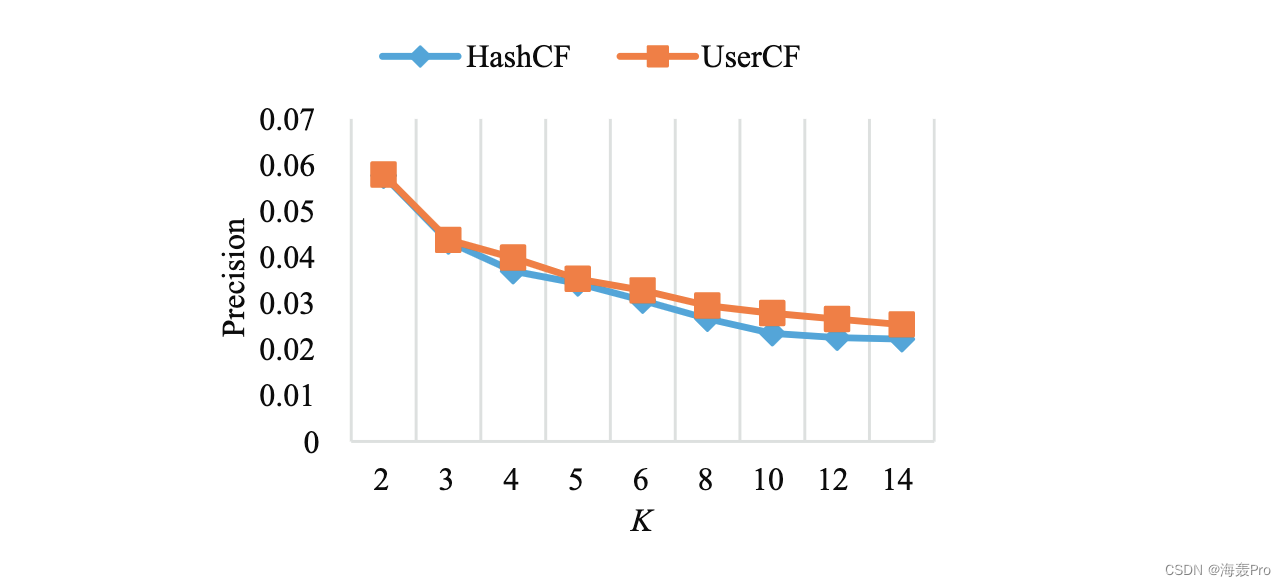
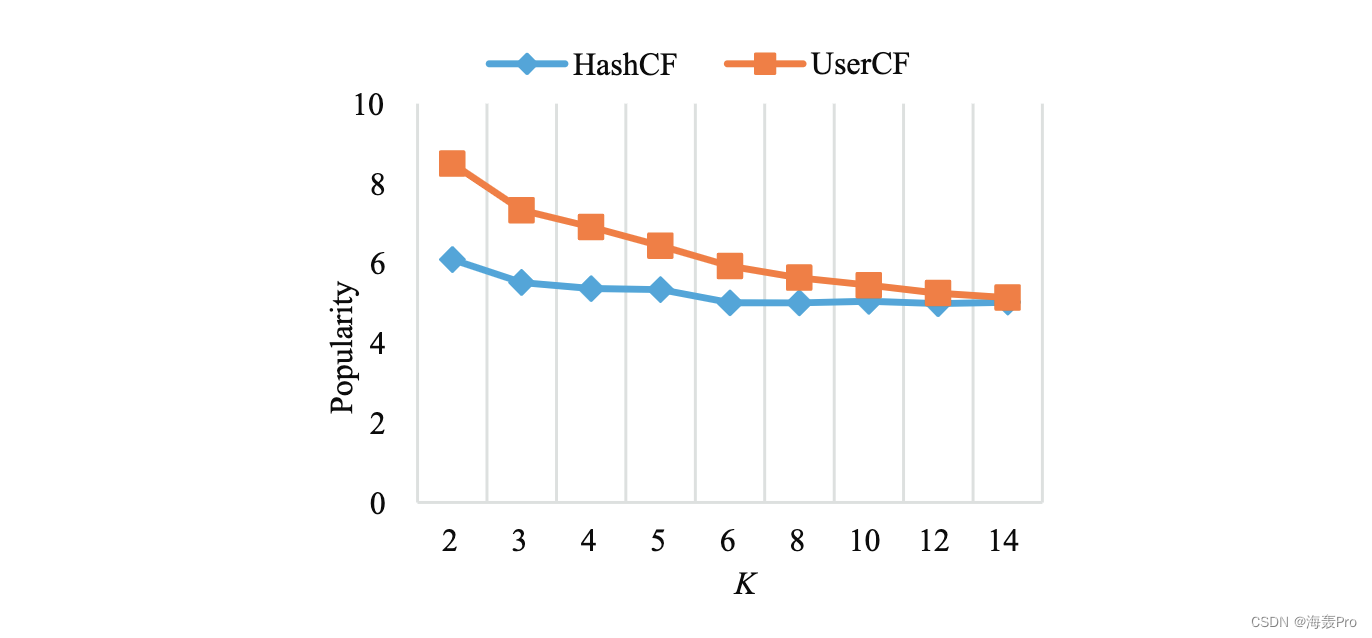
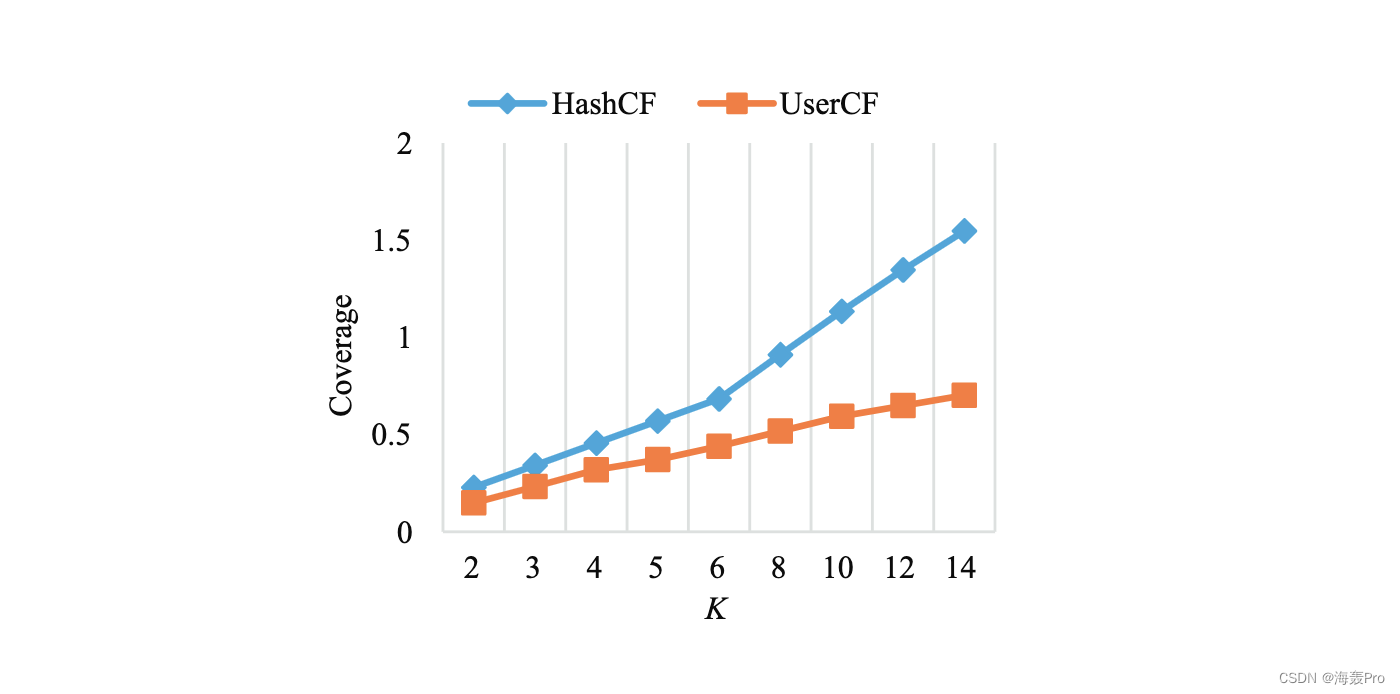
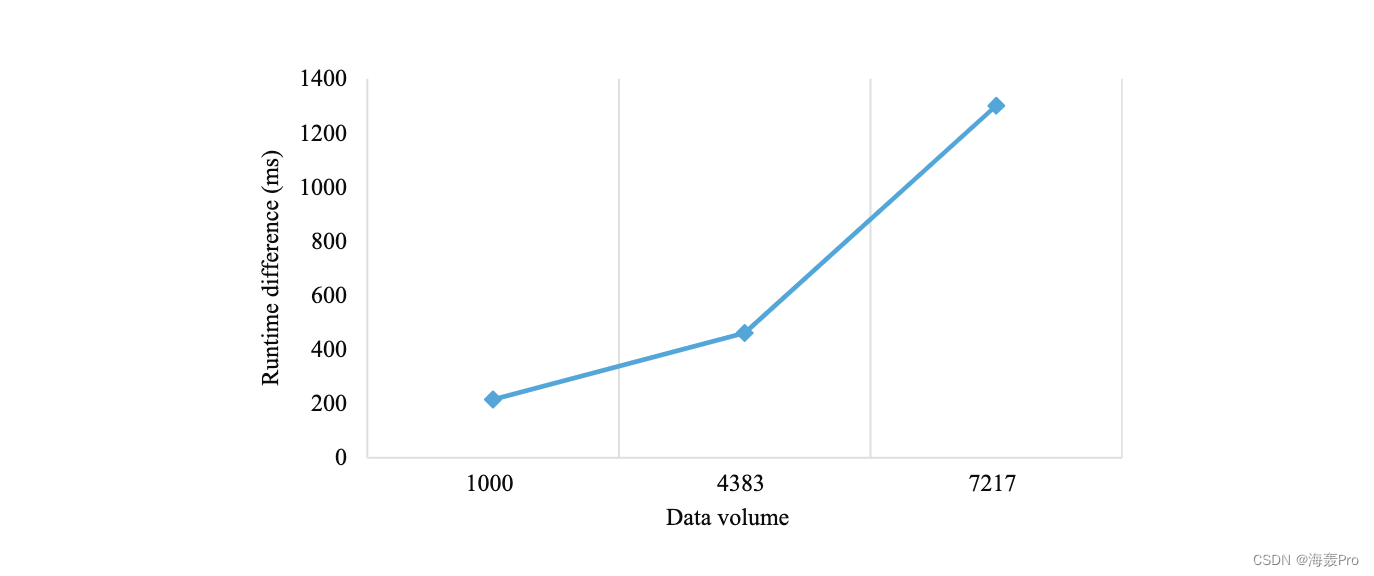
5. Discussion and conclusions
在电子商务中,用户行为大数据中普遍存在的现象是长尾数据的幂律分布。一个有价值的研究课题是如何利用幂律分布来提高推荐系统的性能,即如何充分利用分布的头部和长尾数据进行个性化推荐。本文试图为将幂律分布引入旅游长尾推荐提供一种思路。基于新浪微博签到数据,对用户出行行为的幂律性质进行分析,提出一种结合幂律分布和LSH的改进推荐算法。实验结果表明,我们提出的算法可以增加推荐的多样性,显着提高计算效率。
本文在以下几个方面对TRSs的理论研究做出了贡献。一方面,理想的 TRS 应该为目的地/景点提供多样化的推荐,而不仅仅是推荐热门景点。我们的论文表明,根据项目流行度的分布为不同的位置或目的地分配权重可以更好地解决多样性问题,为解决 TRS 中的多样性问题提出了一个新的研究方向。另一方面,响应时间也是评价TRSs性能的重要标准。通过将LSH应用于用户相似度的计算,大大提高了计算效率,有效解决了降维和冷启动问题,为进一步实现动态旅游推荐提供了可能。
此外,我们的研究结果为旅游领域的长尾推荐提供了一些实际意义。首先,可以利用数据分布或特征来解决推荐结果过于狭隘、缺乏偶然性的问题,为用户提供更广泛的选择,提升用户体验。此外,通过向用户展示更多的小众旅游目的地,帮助商家在长尾或冷启动目的地挖掘更多价值并获得更多收益。其次,OSNs中的用户签到数据可用于预测用户位置,为后续推荐旅游目的地/景点提供依据。
但本文仍存在一些局限性
- 首先,我们只是验证了幂律特性在旅游推荐场景中的可行性和价值。在进一步研究中应考虑更多类型的数据集和应用场景
- 其次,LSH在降低计算复杂度的同时损失了精度,并且LSH得到的哈希表可能会消耗大量存储空间,这有待进一步研究解决
- 第三,我们简单地对长尾部分的非活跃用户进行随机推荐。该方法过于粗糙,需要进一步研究对不活跃用户的推荐。
结语
文章仅作为个人学习笔记记录,记录从0到1的一个过程
希望对您有一点点帮助,如有错误欢迎小伙伴指正

- 点赞
- 收藏
- 关注作者


评论(0)