@TOC

一、堆

1.概念

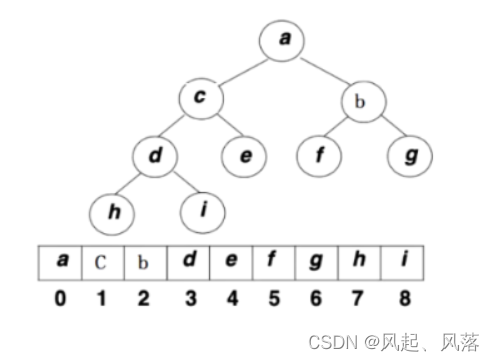
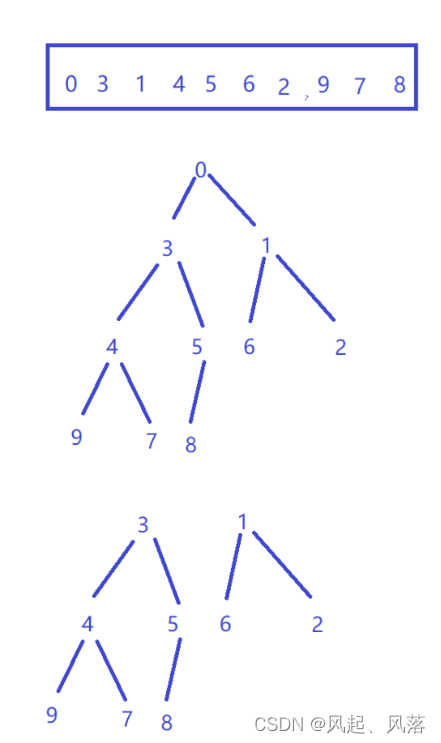
堆的物理结构(我们能看到的)是一个数组
堆的逻辑结构(我们想象出来的)是一个完全二叉树

2.特性

1.结构性：用数组表示完全二叉树
2.有序性: 任一结点的关键字是其子树所有结点的最大值(最小值)
而拥有最大值在顶叫做 大堆
拥有最小值在顶叫做 小堆

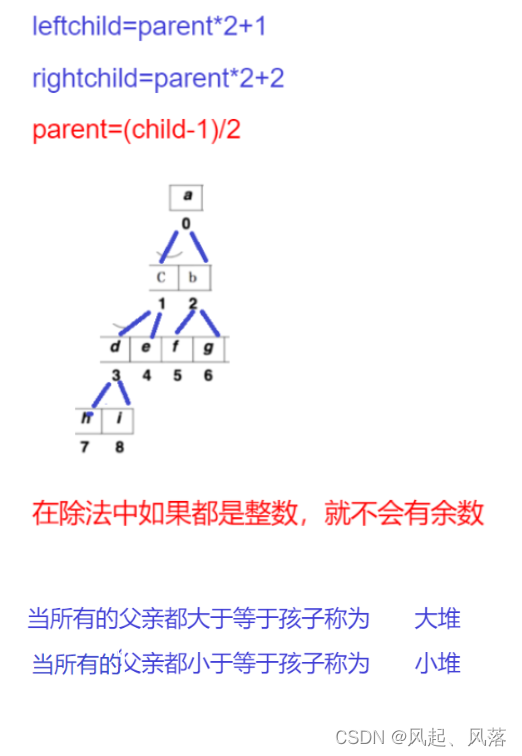
3. 父子结点

因为都是由数组表示的完全二叉树
而数组对应下标
左孩子下标 =父亲节点下标*2+1
右孩子下标 =父亲节点下标*2+2

二、向下调整算法

1.概念

向下调整算法
以小堆为例，
当满足左子树与右子树都是小堆时
从根节点开始
取左右孩子小的那个，与父亲比较，如果比父亲小就交换
然后往下调，以此时的child赋值给parent，
直到调到叶节点就结束

2. 实现

void justdown(int* a, int n, int root)//向下调整算法 ——建堆  小堆
{
	int parent = root;
	int child = parent * 2 + 1;//假设左右孩子小的是左孩子
	while (child<n)//child作为下标小于元素个数就成立，否则数据不存在
	{
		if (a[child + 1] < a[child]&&child+1<n)//作为完全二叉树存在，有可能只存在左子树，而不存在右子树
		{
			child++;//如果左孩子大于右孩子，设小的为右孩子
		}
		if (a[child] < a[parent])//孩子小于父亲,两者就交换
		{
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else//孩子比父亲大 就结束循环  因为左右子树都是小堆 
		{
			break;
		}
	}
}

三 、堆排序的实现

1.建堆

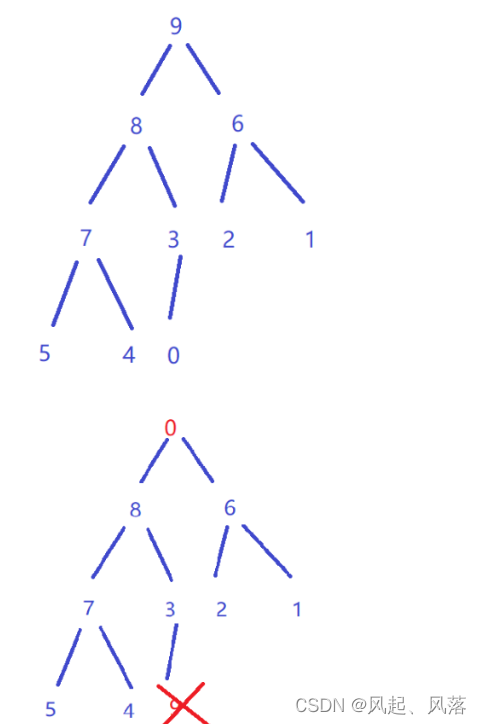
以大堆为例
若发现左子树与右子树不是大堆，则不能直接使用向下调整算法
可以倒着从最后一颗子树开始调 ,使其变成左右子树都是大堆
但是由于叶节点调并由实际作用，所以从倒数第一个非叶子树开始调 ，而正好都是用数组下标表示的，每次减一，都会达到前一个数的位置。
元素个数为n，最后一个数的下标为n-1，0作为8的左子树，8就为(n-1-1)/2

2. 排序

以升序为例
正常来说，我们排升序都应该想到是用小堆，
但是会存在一个问题

建小堆，我们应该把最小数放在堆顶，这个数已经被选出来了，然后在剩下的数中在去选数，此时的树的结构已经乱了，必须重新建堆才能选出下一个数，建堆的时间复杂度是O(N)
这时的时间复杂度为O(N-1) N-2 N-3 N-4…
最后建堆选序的时间复杂度为O(N^2)
对比其他排序这样都没有效率

所以我们采用大堆排升序
使用大堆可以不改变二叉树本身的结构
将 堆顶与最后一个数交换 ，这样最大的数就排到最后了
再将前n-1个数再次使用向下调整算法，找到次大的数 ，与倒数第二个数交换
直到有一个数时停止

3.代码实现

void justdown(int* a, int n, int root)//向下调整算法 ——建堆  大堆
{
	int parent = root;
	int child = parent * 2 + 1;//假设左右孩子大的是左孩子
	while (child < n)//child作为下标小于元素个数就成立，否则数据不存在
	{
		if (a[child + 1] > a[child] && child + 1 < n)//作为完全二叉树存在，有可能只存在左子树，而不存在右子树
		{
			child++;//如果左孩子大于右孩子，设大的为右孩子
		}
		if (a[child] > a[parent])//孩子大于父亲,两者就交换
		{
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else//孩子比父亲小 就结束循环  因为左右子树都是大堆 
		{
			break;
		}
	}
}
void heapsort(int* a, int n)
{
	int i = 0;
	for (i = (n - 1 - 1) / 2; i >= 0; i--)//(n-1-1)/2是从叶节点的上一个父节点开始，

	{
		justdown(a, n, i);//因为实际是一个数组,所以每次减一都往前调一个下标位置
	}
	int end = n - 1;
	while (end > 0)//多于一个值时就进行
	{
		swap(&a[0], &a[end]);//排升序用大堆  
		justdown(a, end, 0);
		end--;
	}
}

四、堆排序的时间复杂度

1.建堆的时间复杂度 O(N)

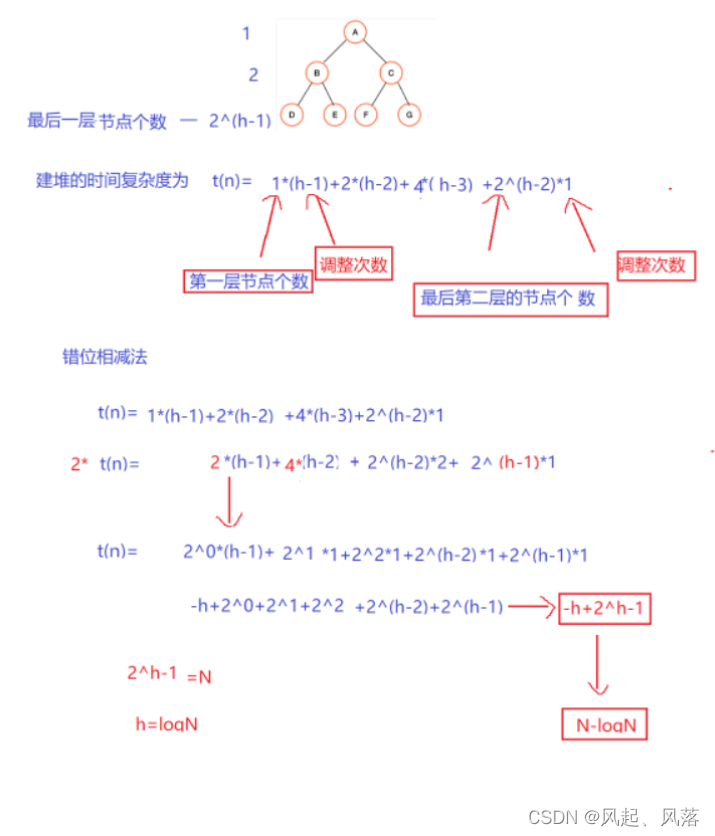
2.排序中运用向下调整算法 ,向下调整算法需要调整高度次h
2^h -1 =N h=log N 时间复杂度为O(logN)
不太懂高度计算的 二叉树的详细图解

堆排序的整体时间复杂度为 O(N*log N)