在去年疫情严重的时候，曾看见有人用数学建模的方式来模拟预测疫情的变化。其中，模拟病毒的传染过程，运用了元胞自动机的方法。这种方法并不难理解，本篇内容将来介绍这种方法。

定义

元胞自动机(cellular automata)是一种时间、空间、状态都离散，空间相互作用和时间因果关系为局部的网格动力学模型，具有模拟复杂系统时空演化过程的能力。

元胞自动机的构成

元胞自动机由元胞、元胞空间、元胞邻居和元胞规则四部分组成。
下面这幅图很容易理解这几个概念。

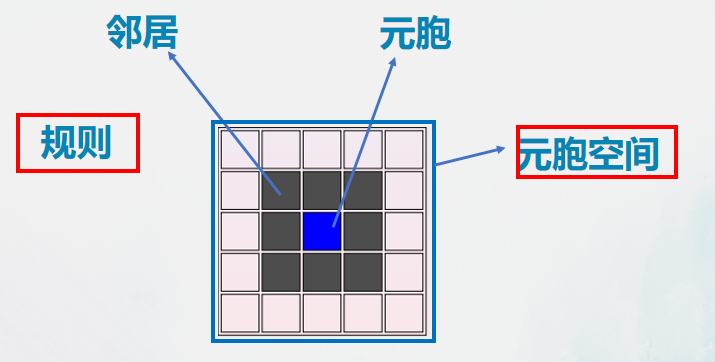
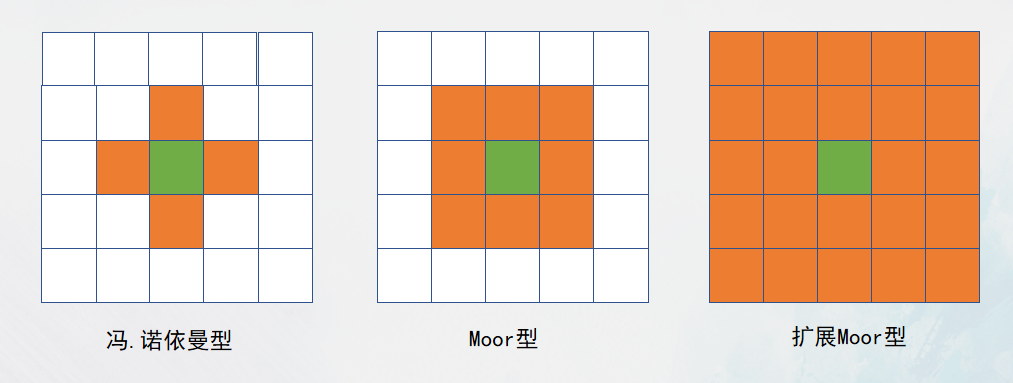
邻居

对邻居的理解并不固定，通常来说的邻居便是指冯诺伊曼型。

边界条件

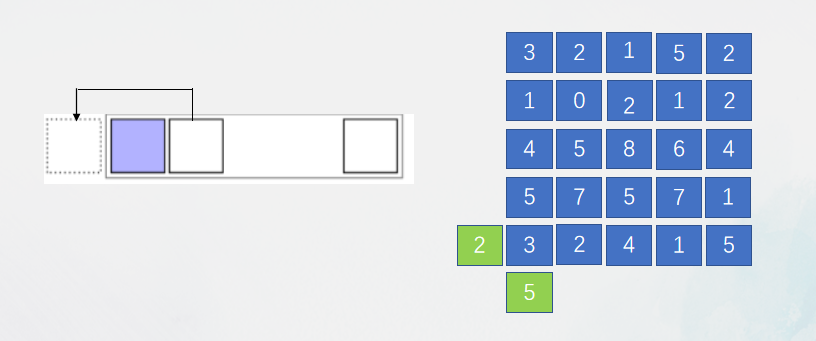
理论上，元胞空间是无限的，实际应用中无法达到这一理想条件。为了给元胞空间边界上的元胞拥有规则所需要的邻居，就需要构造出一些虚拟的邻居。

1、固定型边界
固定型：在边界部分指定一个数。

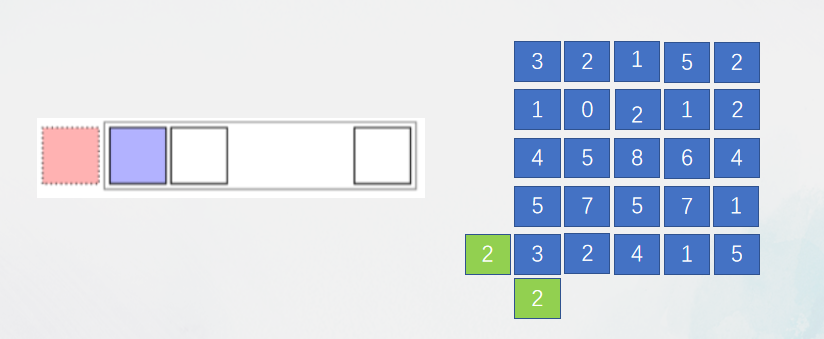
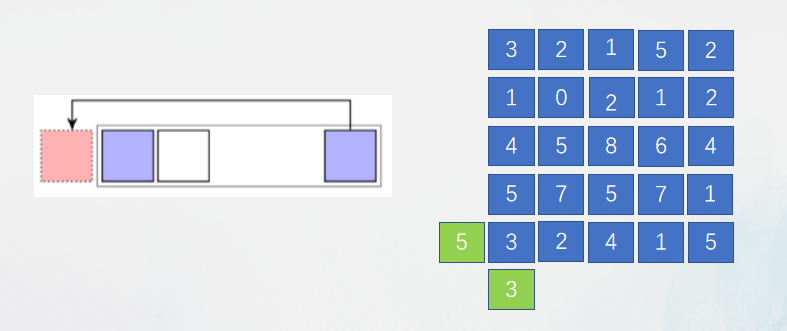
2、周期型边界
周期型，将最右侧的邻居当作虚拟的左侧。

3、绝热型边界
绝热型：自己是自己的邻居。

4、映射型边界
映射型：以自己为中心进行对称。

规则

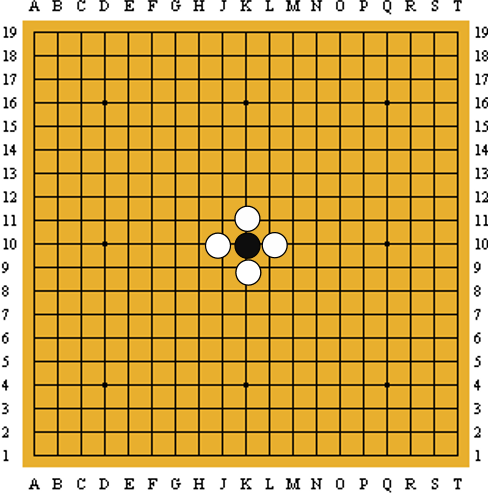
根据元胞当前状态及邻居的状态来决定下一时刻该元胞状态。元胞自动机根据规则进行局部元胞间的相互作用从而引起全局的变化。

规则可以多种多样，比如围棋中，被包围的棋子状态由黑/白转为空，即一种规则。

元胞自动机与matlab

application/pdf 4星 超过85%的资源 276KB

下载

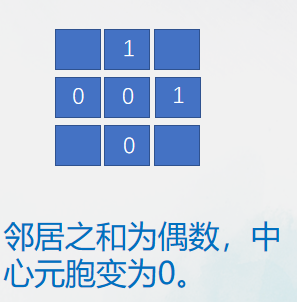
实例一：奇偶规则

定义元胞有两种状态0/1。
定义规则如下：


matlab代码：关键代码已注释

clc
clear all;
n=200;
Se=zeros(n); 
Z=zeros(n)
Se(n/2-2:n/2+2,n/2-2:n/2+2)=1;  %初始化中心几个点为1。
Ch=imagesc(cat(3,Se,Z,Z));  % 生成图像，cat函数用来改变颜色，美化图像
axis square                % 增加边框
Sd=zeros(n+2);           % Sd代表包含虚拟邻居的网格图
while(1)
    Sd(2:n+1,2:n+1)=Se;
    % 制定相应变化规则
    sum=Sd(1:n,2:n+1)+Sd(3:n+2,2:n+1)+Sd(2:n+1,1:n)+Sd(2:n+1,3:n+2);
    Se=mod(sum,2);
    % 更新地图点
    set(Ch,'cdata',cat(3,Se,Z,Z)) 
    pause(0.05)
end
   figure

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
 

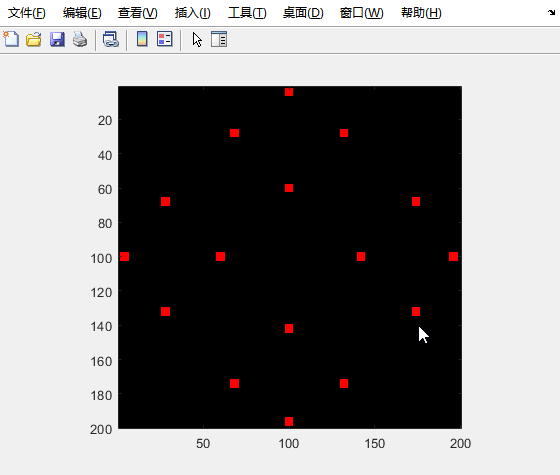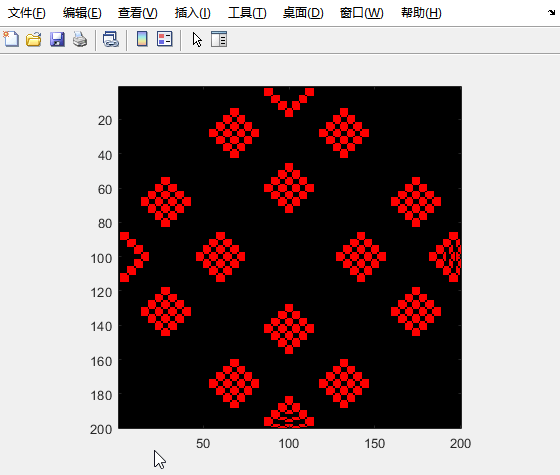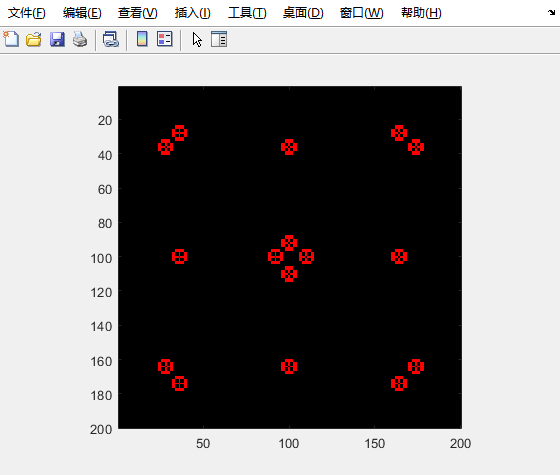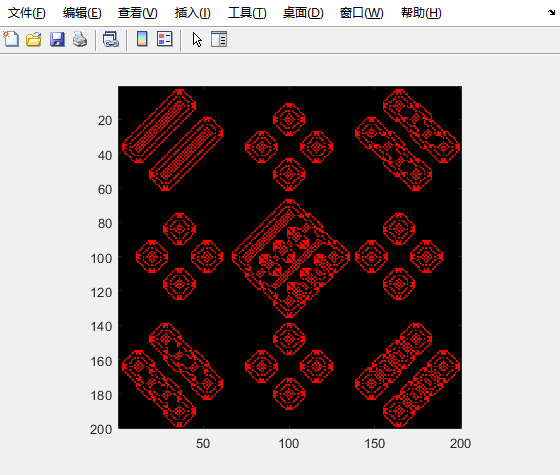
演示效果：

实例二：澳洲火灾

澳洲火灾是2021年美赛的B题。
这里简化处理，森林火灾元胞自动机模型定义在正方形网格上，元胞有三种状态：树，火和空地。不考虑风的影响。

matlab代码：

clc
clear
n = 300;                           % 定义表示森林的矩阵大小
Plight = 5e-6; Pgrowth = 1e-2;     % 定义闪电和生长的概率  
UL = [n,1:n-1]; DR = [2:n,1];      % 定义上左，下右邻居
veg=zeros(n,n);                    % 初始化表示森林的矩阵
imh = image(cat(3,veg,veg,veg));   % 可视化表示森林的矩阵
% veg = 空地为0 着火为1 树木为2
for i=1:3000 
    sum =(veg(UL,:)==1) + (veg(:,UL)==1)+(veg(:,DR)==1) +  (veg(DR,:)==1);  % 计算出所有格子有几个邻居是着火的
% 根据规则更新森林矩阵：是否树=是否树-是否着火的树+是否新生的树（0-1运算）
    veg = 2*(veg==2) - ( (veg==2) & (sum>0 |(rand(n,n)<Plight)) ) +2*((veg==0) & rand(n,n)<Pgrowth) ;  
    set(imh, 'cdata', cat(3,(veg==1),(veg==2),zeros(n)) )
    drawnow                         % 可视化表示森林的矩阵
end

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
 

演示效果：

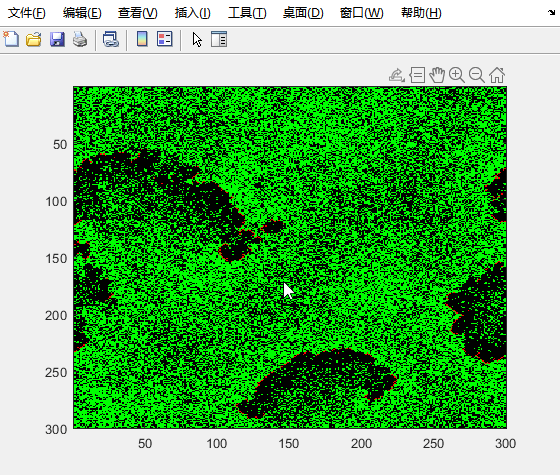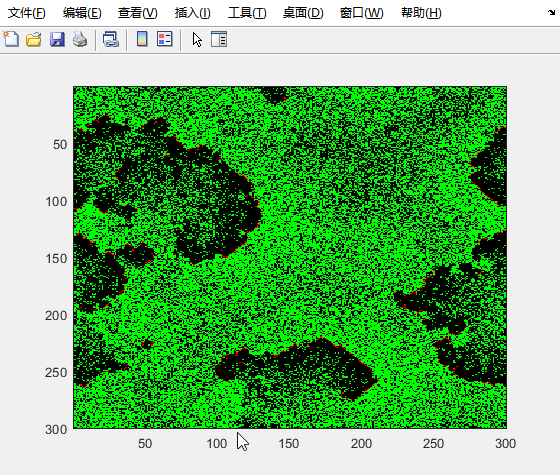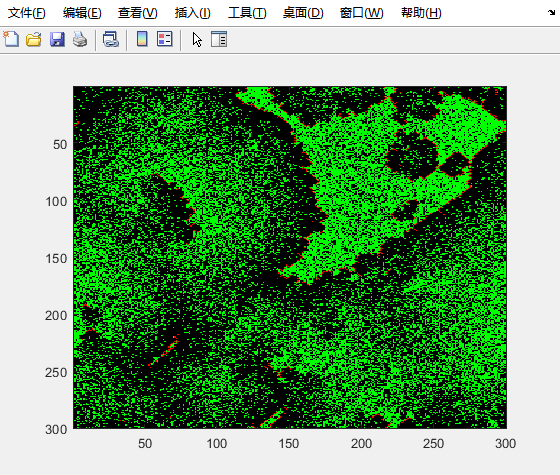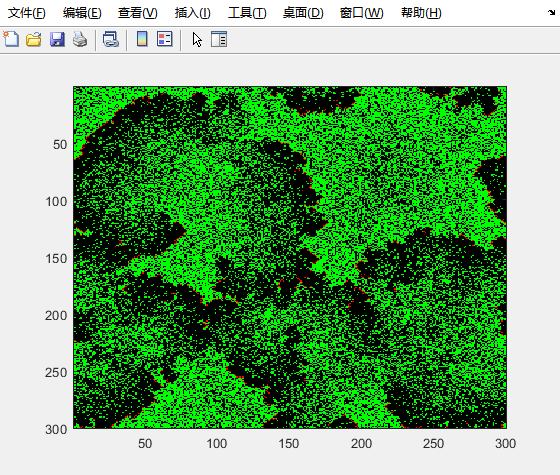
总结

元胞自动机

优点：理论简单，容易理解，效果壮观。
缺点：动图很难在论文中充分展现，且当演变规则复杂时，需要一定编程能力。

参考资料

【2021美赛赛前培训】【元胞自动机】

文章来源: zstar.blog.csdn.net，作者：zstar-_，版权归原作者所有，如需转载，请联系作者。

原文链接：zstar.blog.csdn.net/article/details/120187393