作者：半身风雪
简介：移动开发全栈领域工作者

@TOC

一、树

1.1、什么是树

       因为在客观世界里，有许多的事务，存在着细致的划分，比如下图：在我们中国，存储在各个省市的划分。

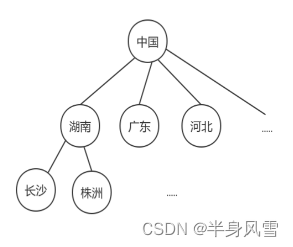
那为什么要采取树这种结构呢？
       我们可以看到，树这种结构在管理层次里面，它的管理效率更高。因为我们可以根据树的层次去更快的查找数据，比如：中国-湖南-广东-长沙等。树的层次管理具有更高的效率。

1.2、树的定义

树(Tree)：N个结点构成的有限集合。

• 树中有一个称为“根(Root)”的特殊结点。
• 其余结点可以分为若干个互不相交的树，称为原来结点的“子树”

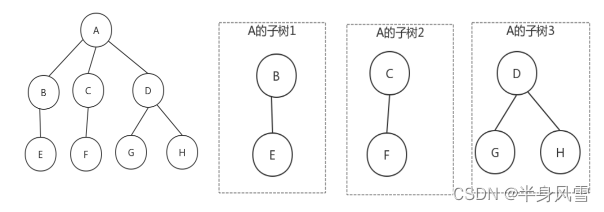
从上图中，我们可以看出，A是树的根，B、C、D 都是A的是子树

1.3、树的常用基本术语

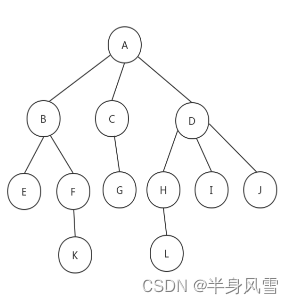
一起来看一下上面的树，我们可以总结出：

• 结点的度：结点的子树个数。
• 树的度：树中所有结点中最大的度。
• 叶结点：度为0的结点。
• 父结点：所有子树的结点是其子树的根结点的父结点。
• 子结点：若A是B的父结点，B就是A的子结点。

1.4、树与非树

我们先来看一组错误的树：

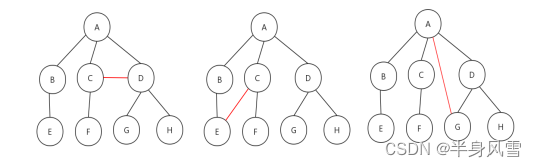
上图中的三种情况，都不能称之为树。为什么呢？

• 子树是不相交的。
• 除了根结点之外，每个结点有且只有一个父节点。
• 一个N个结点的树，只有N-1条边

下面来看一个真正的树：

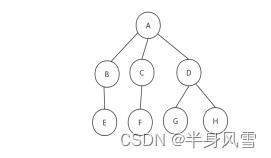
二、二叉树

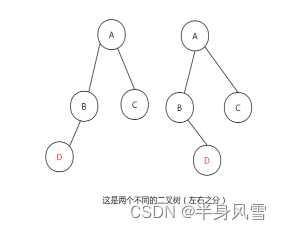
2.1、什么是二叉树

• 度为2的树（树中所有结点中最大的度）。
• 子树有左右之分。

三、Huffman 编码及实现

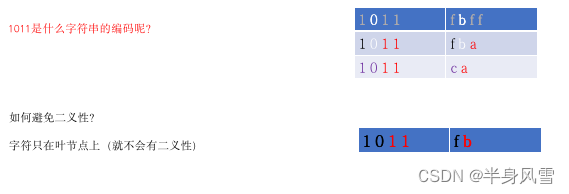
3.1、编码问题

给你一段字符串，如何对字符串进行编码，可以使得该字符串的编码存储空间最少？

假设一段文本，包含58个字符，并且由以下7个字符构成:a,b,c,d,e,f,g；这7个字符出现的频次不同，如何对这7个字符进行编码，使得总编码空间最小。

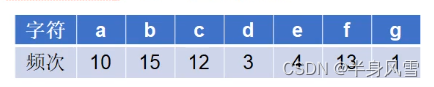
我们一起来分析一下：

1. 用等长ASCII编码：58 x 8 = 464位。
2. 用等长3位编码：58 x 3 = 174位。
3. 不等长编码：出现频次高的字符用的编码短些，出现频次低的编码长些。

编码长度：10 x 3 + 15 x 2 + 12 x 2 + 5 x 3 + 4 x 4 + 13 x 2 + 5 x 1 = 146位。

3.2、使用二叉树解决编码问题

使用二叉树进行编码
二叉树左右分支：0、1
根据上图，我们可以发现，编码对应的字符串是：

b 编码 0
f 编码 1
c 编码 10
1 编码 11

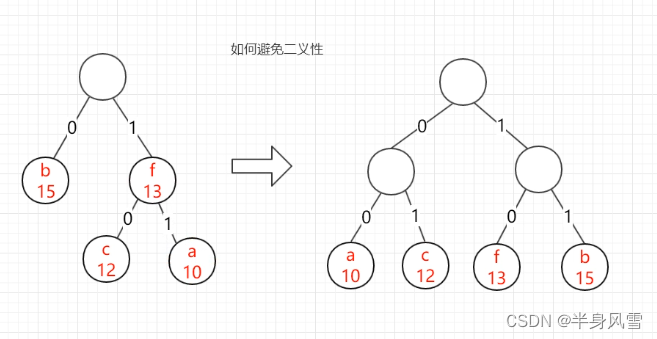
3.3、哈夫曼树的构造

哈夫曼树：构建一颗二叉树，该树的带权路径长度达到最小，称为最优二叉树，也称为哈夫曼树(Huffman Tree)。

构造方式：每次把权值最小的两颗二叉树合并。左结点权值比右结点小。

四、哈夫曼树代码实现

public class HuffmanTree {
    //节点
    public static class Node<E> {
        E data; //数据
        int weight; //权重
        Node leftChild; //左子节点
        Node rightChild;//右子节点

        public Node(E data, int weight) {
            super();
            this.data = data;
            this.weight = weight;
        }

        public String toString() {
            return "Node[" + weight + ",data=" + data + "]";
        }
    }

    public static void main(String[] args) {
        List<Node> nodes = new ArrayList<Node>();
        //把节点加入至list中
        nodes.add(new Node("a", 10));
        nodes.add(new Node("b", 15));
        nodes.add(new Node("c", 12));
        nodes.add(new Node("d", 3));
        nodes.add(new Node("e", 4));
        nodes.add(new Node("f", 13));
        nodes.add(new Node("g", 1));
        //进行哈夫曼树的构造
        Node root = HuffmanTree.createTree(nodes);
        //打印哈夫曼树
        printTree(root);

    }

    /**
     * 构造哈夫曼树
     *
     * @param nodes
     *            节点集合
     * @return 构造出来的哈夫曼树的根节点
     */
    private static Node createTree(List<Node> nodes) {
        //如果节点node列表中海油2个和2个以上的节点
        while(nodes.size()>1){
            //什么是最小的，list表进行排序，增序的方式， 0,1，
            sort(nodes);//排序方式是增序的
            Node left = nodes.get(0);//权重最小的
            Node right = nodes.get(1);//权重第二小的
            //生成一个新的节点（父节点），父节点的权重为两个子节点的之和
            Node parent = new Node(null,left.weight+right.weight);
            //树的连接，让子节点与父节点进行连接
            parent.leftChild = left;
            parent.rightChild = right;
            nodes.remove(0);//删除最小的
            nodes.remove(0);//删除第二小的。
            nodes.add(parent);
        }
        return nodes.get(0); //返回根节点
    }
    /**
     * 冒泡排序，用于对节点进行排序（增序排序）
     *
     * @param nodes
     */
    public static void sort(List<Node> nodes) {
        if (nodes.size() <= 1)
            return ;
        /*循环数组长度的次数*/
        for (int i = 0; i < nodes.size(); i++){
            /*从第0个元素开始，依次和后面的元素进行比较
             * j < array.length - 1 - i表示第[array.length - 1 - i]
             * 个元素已经冒泡到了合适的位置，无需进行比较，可以减少比较次数*/
            for (int j = 0; j < nodes.size() - 1 - i; j++){
                /*如果第j个节点比后面的第j+1节点权重大，交换两者的位置*/
                if (nodes.get(j + 1).weight < nodes.get(j).weight) {
                    Node temp = nodes.get(j + 1);
                    nodes.set(j+1,nodes.get(j));
                    nodes.set(j,temp);
                }
            }
        }
        return ;
    }

    /*

     * 递归打印哈夫曼树(先左子树，后右子树打印)
     */

    public static void printTree(Node root) {
        System.out.println(root.toString());
        if(root.leftChild !=null){
            System.out.print("left:");
            printTree(root.leftChild);
        }
        if(root.rightChild !=null){
            System.out.print("right:");
            printTree(root.rightChild);
        }
    }
}