【优化求解】基于matlab遗传算法结合粒子群算法求解单目标优化问题【含Matlab源码 1659期】

一、GA-PSO混合优化算法的基本思想

对于遗传算法来讲, 传统的遗传算法中变异算子是对群体中的部分个体实施随机变异, 与历史状态和当前状态无关。而粒子群算法中粒子则能保持历史状态和当前状态。遗传算法的进化初期, 变异有助于局部搜索和增加种群的多样性;在进化后期, 群体已基本趋于稳定, 变异算子反而会破坏这种稳定。变异概率过大会使遗传模式遭到破坏, 过小又会使搜索过程缓慢甚至停滞不前。本文通过在粒子群算法中引入遗传算法的交叉操作, 改进种群分割策略, 且用粒子群算法重构变异算子来进行算法的改进。本文所提的混合算法主要就是从用遗传算法来模拟粒子群算法的角度出发, 利用粒子群算法来重构遗传算法算子和进行种群分割。从宏观上来看, 其行为是粒子群算法;从微观来看, 其行为是遗传算法, 从而构成遗传-粒子群混合算法。下面主要介绍一下引入的交叉和变异算子及变异算子。

1 交叉算子
设GA-PSO混合算法总的进化代数为T, 当算法进化到第t代时, 总的种群设为∏t={x1t, …, xit, …, xnt}, (1≤i≤n) , n为种群规模, xit为单个粒子, 且对于任意i, (1≤i≤n) , 都有xit≤xjt成立, 即∏t有序。由于所讨论的混合算法的个体编码采用了实值编码, 且该算法主要针对于数值优化问题故交叉算子采用了算术交叉。
假设在两个个体xit, xjt (i≠j) 之间进行算术交叉, 则交叉运算后所产生的两个新个体是:

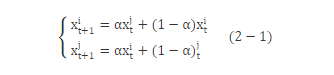
式 (2-1) 中, α为一参数, 若α是一个常数, 此时所进行的交叉运算称为均匀算术交叉;也可以是一个由进化代数决定的变量, 此时进行的是非均匀算术交叉。

2 变异算子
在GA-PSO混合算法中利用粒子群算法的进化公式来重构变异算子, 让个体依据自身迄今最优解和子种群内迄今最优解以及个体进化的速度来决定变异方向和幅度, 使个体在进化的过程中可以将其进化的历史作为导向标。具体实现如下:用xit代替粒子群算法中的xid (第i个粒子在D维空间的位置) , 用∏t中第i位历史最优fimax对应的ximax代替粒子群算法中的Pid (个体最优) , 用子种群的历史最优Fjmax (j为该粒子团在子种群中的位置) 对应的Xjmax代替Pgd (全局最优) , 用ximax的累计差的算术平均Δximax来代替vid。其中ximax的累计差由 (2-2) 式求的:

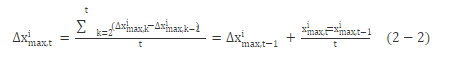
则引入变异算子后的粒子群算法粒子更新公式为

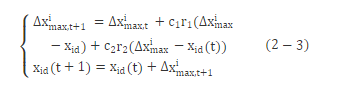
通过上述公式, 我们可以看到在第一部分通过权重因子c1, c2和随机数r1, r2以及信息反馈Ximax预测了变异的幅度和方向;第二部分则具体实施了变异操作。因此, 粒子群算法变异操作具备了自学习能力, 在变异之前的预测, 也使变异操作不再是简单的随机变异, 而是提高单个粒子对进化环境适应能力的变异。

GA-PSO混合优化算法流程图如图2-1,

图2-1 GA-PSO流程图

二、部分源代码

%% GA 优化 PSO
%% 清空环境
clc;
clear
close all
%% 参数初始化
lenchrom=7;    %字符串长度（个体长度），染色体编码长度
pc=0.7;        %设置交叉概率，本例中交叉概率是定值，若想设置变化的交叉概率可用表达式表示，或从写一个交叉概率函数，例如用神经网络训练得到的值作为交叉概率
pm=0.3;        %设置变异概率，同理也可设置为变化的

%粒子群算法中的两个参数
c1 = 1.49445;
c2 = 1.49445;

maxgen=20;   % 进化次数  
popsize=30; %种群规模

%粒子更新速度
Vmax=1;
Vmin=-1;

%种群
popmax=50;
popmin=-50;

% 变量取值范围
bound=[popmin popmax;popmin popmax;popmin popmax;popmin popmax;popmin popmax;popmin popmax;popmin popmax];  %变量范围

% 优化粒子数目
par_num=7;

%% 产生初始粒子和速度
for i=1:popsize
    %随机产生一个种群
    pop(i,:)=popmax*rands(1,par_num);    %初始种群
    V(i,:)=rands(1,par_num);  %初始化速度
    %计算适应度
    fitness(i)=fun(pop(i,:));   %染色体的适应度
end

%找最好的染色体
[bestfitness bestindex]=min(fitness);
zbest=pop(bestindex,:);   %全局最佳
gbest=pop;    %个体最佳
fitnessgbest=fitness;   %个体最佳适应度值
fitnesszbest=bestfitness;   %全局最佳适应度值

%% 迭代寻优
for i=1:maxgen
    i
    for j=1:popsize
        
        %速度更新 PSO选择更新
        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,find(V(j,:)>Vmax))=Vmax;
        V(j,find(V(j,:)<Vmin))=Vmin;
        
        %种群更新 PSO选择更新
        pop(j,:)=pop(j,:)+0.5*V(j,:);
        pop(j,find(pop(j,:)>popmax))=popmax;
        pop(j,find(pop(j,:)<popmin))=popmin;
        
        % 交叉操作 GA
        GApop=Cross(pc,lenchrom,pop,popsize,bound);
        
        % 变异操作 GA变异
        GApop=Mutation(pm,lenchrom,GApop,popsize,[i maxgen],bound);
        
        pop=GApop; % GA pop --> PSO pop
      
        % 适应度值 --> 约束条件
         if 0.072*pop(j,1)+0.063*pop(j,2)+0.057*pop(j,3)+0.05*pop(j,4)+0.032*pop(j,5)+0.0442*pop(j,6)+0.0675*pop(j,7)<=264.4
            if 128*pop(j,1)+78.1*pop(j,2)+64.1*pop(j,3)+43*pop(j,4)+58.1*pop(j,5)+36.9*pop(j,6)+50.5*pop(j,7)<=69719
                    fitness(j)=fun(pop(j,:));
               end
         end

        %个体最优更新
        if fitness(j) < fitnessgbest(j)
            gbest(j,:) = pop(j,:);
            fitnessgbest(j) = fitness(j);
        end
        
        %群体最优更新
        if fitness(j) < fitnesszbest
            zbest = pop(j,:);
            fitnesszbest = fitness(j);
        end
        
    end
    
    yy(i)=fitnesszbest;     
end

%% 结果
disp '*************best particle number****************'
zbest

%%
plot(yy,'linewidth',2);
grid on
title(['适应度曲线  ' '终止代数＝' num2str(maxgen)]);
xlabel('进化代数');ylabel('适应度');




  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
  
76
  
77
  
78
  
79
  
80
  
81
  
82
  
83
  
84
  
85
  
86
  
87
  
88
  
89
  
90
  
91
  
92
  
93
  
94
  
95
  
96
  
97
  
98
  
99
  
100
  
101
  
102
  
103
  
104
  
105
  
106
 

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]包子阳,余继周,杨杉著.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社
[2]巩永光.粒子群算法与遗传算法的结合研究[J].济宁学院学报. 2008,29(06)

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/122352272