折线法计数、反射原理

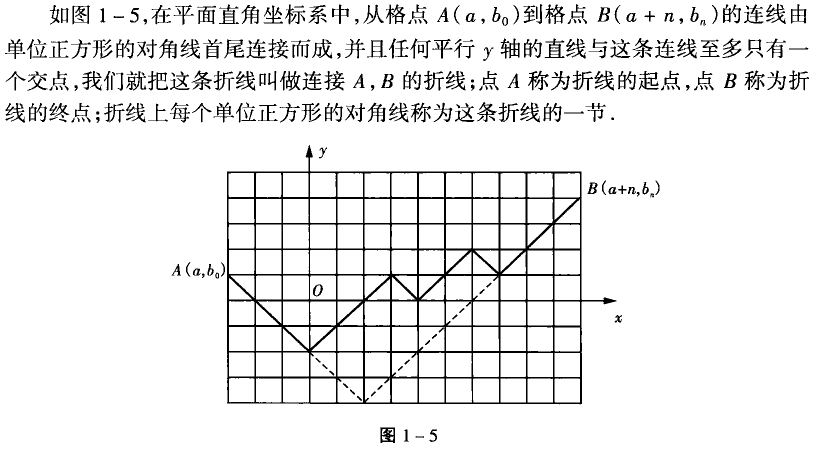
投票问题:

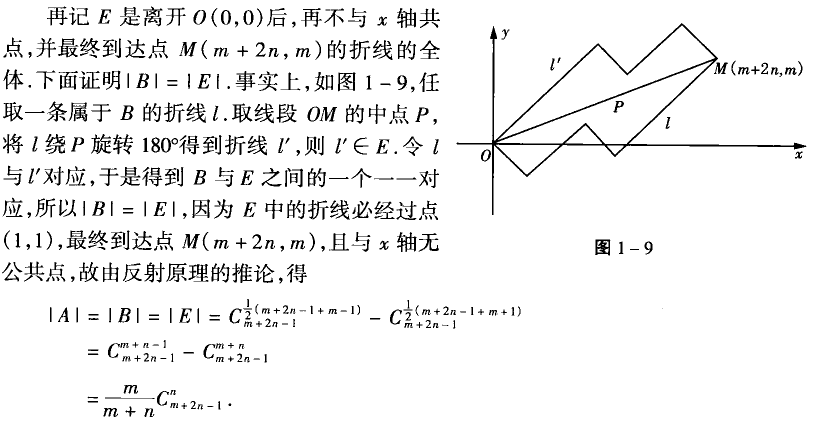
HDU - 1267

Description

......一个字符串由m个H和n个D组成，从左到右扫描该串，如果字符H的累计数总是不小于字符D的累计数,那么，满足条件的字符串总数......有多少......

Input

输入数据包含多个测试实例，每个占一行，由两个整数m和n组成，m和 n 分别表示字符串中H和D的个数。由于我们目前所使用的微机和老美的超级计算机没法比，所以题目给定的数据范围是（1<=n<=m<=20）。 

Output

......每个实例的输出占一行。 

Sample Input

1 1
3 1

Sample Output

1
3

方法一：递推

几乎所有的提交都是这样做的。

  

   

    

     

    
    

     

      #include<iostream>
     
    
   

    

     

    
    

     

      using namespace std;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int main()
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	long long l[21][21];
     
    
   

    

     

    
    

     
	for (int i = 1; i < 21; i++)l[0][i] = 1;
     
    
   

    

     

    
    

     
	for (int i = 1; i < 21; i++)
     
    
   

    

     

    
    

     

      	{
     
    
   

    

     

    
    

     

      		l[i][i] = l[i - 1][i];
     
    
   

    

     

    
    

     
		for (int j = i + 1; j < 21; j++)l[i][j] = l[i - 1][j] + l[i][j - 1];
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
	int m, n;
     
    
   

    

     

    
    

     
	while (cin >> m >> n)cout << l[n][m] << endl;
     
    
   

    

     

    
    

     
	return 0;
     
    
   

    

     

    
    

     

      }
     
    
  
 

方法二：用公式

上面的例一几乎和这个题目一模一样。

结果：(m+n)!/(m+1)!/n!*(m-n+1)

计算这个式子的时候要注意顺序，否则m=3,n=2的情况会算错。

代码：

  

   

    

     

    
    

     

      import java.util.*;
     
    
   

    

     

    
    

     

      import java.math.BigInteger;
     
    
   

    

     

    
    

     

      public class Main {
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
	public static BigInteger f(int k)
     
    
   

    

     

    
    

     

      	{
     
    
   

    

     

    
    

     

      		BigInteger s=new BigInteger("1");
     
    
   

    

     

    
    

     
		for(int i=1;i<=k;i++)s=s.multiply(BigInteger.valueOf(i));
     
    
   

    

     

    
    

     
		return s;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
	
     
    
   

    

     

    
    

     
    public static void main(String[] args) {
     
    
   

    

     

    
    

     
        Scanner cin = new Scanner(System.in);
     
    
   

    

     

    
    

     
        while(cin.hasNext())
     
    
   

    

     

    
    

     

              {
     
    
   

    

     

    
    

     
        	int m=Integer.parseInt(cin.next()),n=Integer.parseInt(cin.next());
     
    
   

    

     

    
    

     

              	BigInteger s=f(m+n).multiply(BigInteger.valueOf(m-n+1)).divide(f(m+1)).divide(f(n));
     
    
   

    

     

    
    

     

                  System.out.println(s.toString());
     
    
   

    

     

    
    

     

              }        
     
    
   

    

     

    
    

     

          }
     
    
   

    

     

    
    

     

      }
     
    
  
 

2份代码都AC了，第一种方法的时间复杂度是O（m*n），第二种是O（m+n）

当然了，时间复杂度和时间不能混为一谈，第一种是0ms AC，第二种是265ms

文章来源: blog.csdn.net，作者：csuzhucong，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/nameofcsdn/article/details/53144666