台湾清华大学概率论笔记一 导论

  在生活中存在着很多的不确定性（随机性）的现象。具体来说，很多事件在未发生之前虽然可以知道结果的集合，但是却无法预测具体的结果是哪个。应用概率论的知识，可以用来预测未来。但随机事件也不一定是和未来相关的，比如把手机丢在了某个位置。
  在生活中，有一些表面上看来没有随机性（确定性），但却真真正正存在着不确定性的事件。如测量身高，不同时刻的测量结果是不同的，测量也会包含测量误差（如仪器的精度）。
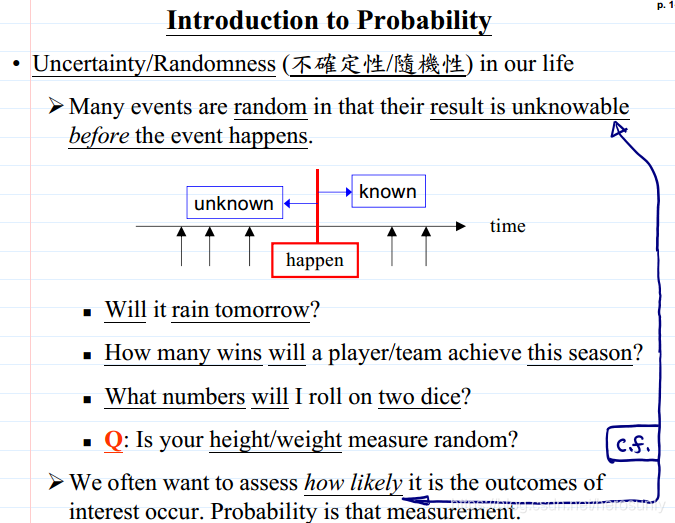
  概率论可以用来对随机性进行测量(how likely)，从而能够更好的处理带有随机性的问题。

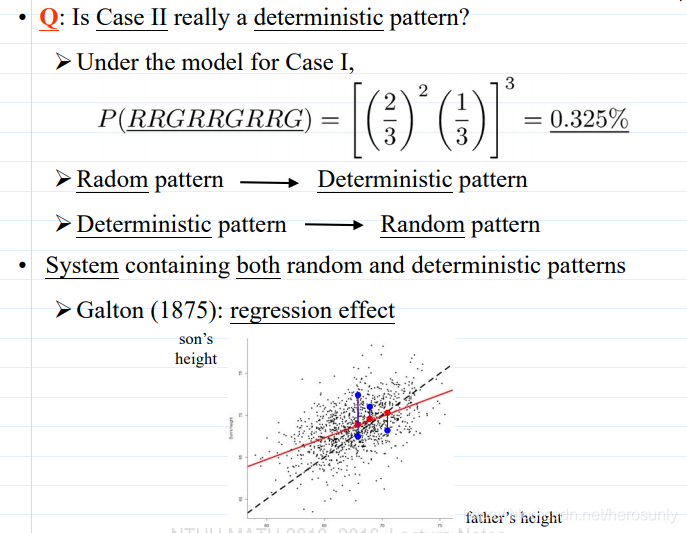
  生活中存在着两大类的事件：随机性事件和确定性事件。其中确定性事件指的是必然发生或者必然不发生的事件。必然事件比如$\mathbf{F}=\mathbf{m}\mathbf{a}$，$2H_2+O_2=2H_{2}O$。人比较习惯处理确定性的事件，学习也是这样，从小到大学的学科绝大多数处理的都是确定性事件。在生活中，我们会把确定性事件称为规律、秩序、信号(有规律)。而把随机性事件称为混乱、噪音（无规律）。#表示的是集合元素的个数。

下图为对随机事件和确定事件的描述方式。
需要注意的是，大括号表示的是集合，即元素之间的顺序不重要。

Cannot read property 'type' of undefined

文章来源: blog.csdn.net，作者：herosunly，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/herosunly/article/details/88743870