一、图像锐化简介

前面讲过图像的滤波操作，即平滑操作，一般情况下图像的噪声和边缘信息是储存在高频段，而图像的平滑操作为了降噪会对高频段的信息进行减弱，因此边缘的信息在这个过程中受到损失，图像变得模糊，而图像的锐化操作相反，是对高频段的信息增强，强化图像的边缘信息，主要用于图像的边缘发现。
在前面的平滑操作中，我们一般是对邻域内的像素值进行加权求和或求平均，类似于积分的操作，使得图像变得模糊，锐化操作则是要将图像变得更加清晰，因此要与平滑操作相反，这里我们需要对邻域进行求微分操作，这是一切的锐化操作的基本的思路。

图像锐化的方法

1.微分法

梯度法：
在介绍梯度法之前，要先了解一下像素值变化曲线，像素值变化曲线是指在图像中画一条扫描线，将扫描线上的像素值变化画成曲线即为像素值变化曲线，通过曲线可计算其梯度，如：


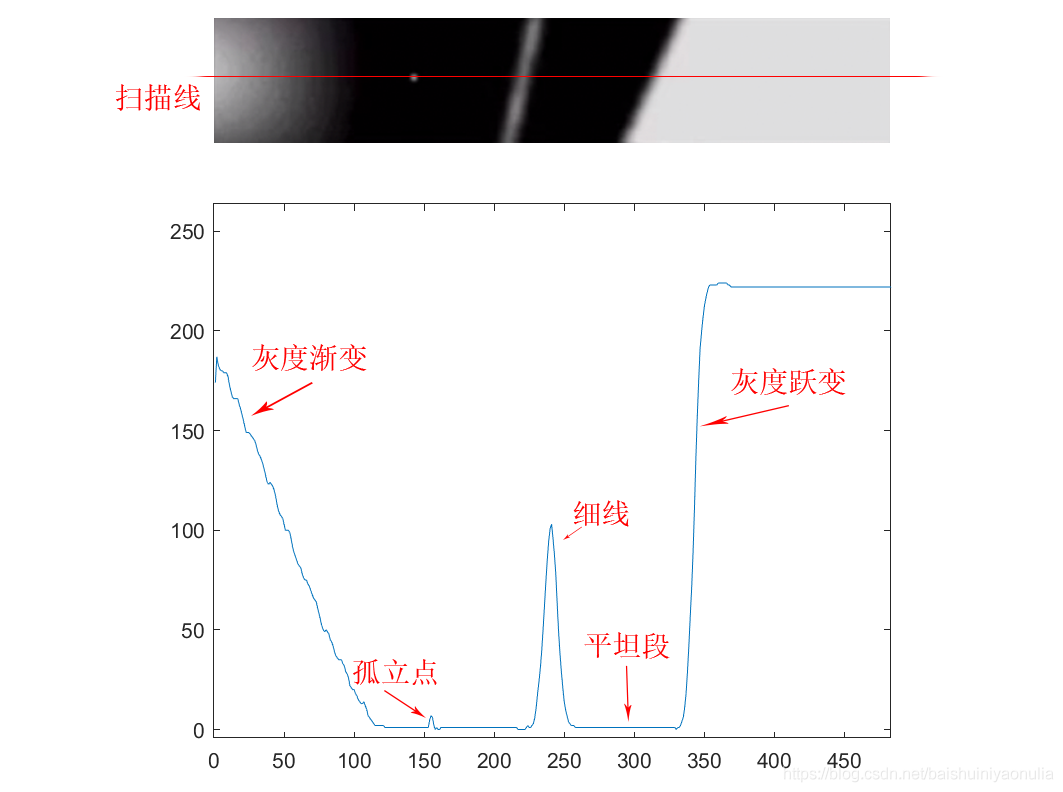
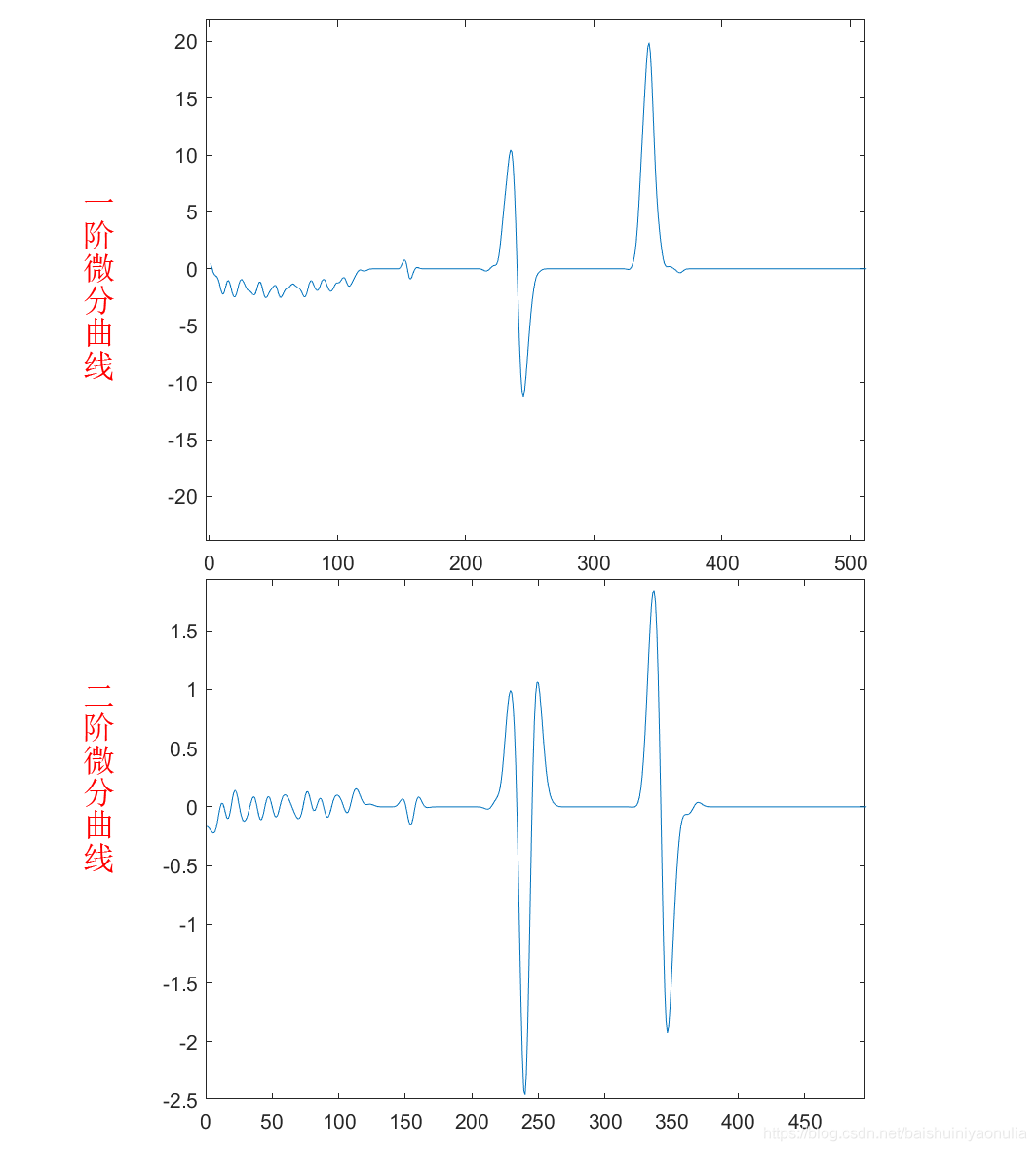
在每一个点处，沿着其梯度的方向是像素值变化最快的方向，梯度的模与像素值之间的差值相当，而在边缘处往往像素值变化最大，而非边缘处像素值变化较小，因此使用梯度的模或其导出的值来代替原有的像素值可以有效得显示出边缘信息，至于连续性不强的或是离散得图像，一般采用差分法来代替梯度的作用


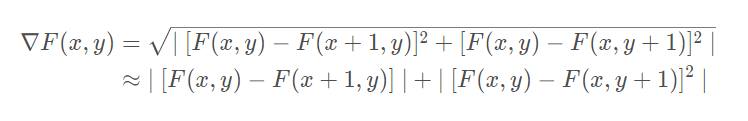
以下是一些用梯度代替像素值（锐化输出）的做法：
（1）直接替代法：即将每一个点梯度的模作为该点的锐化输出：
这种方法虽然简单，但在图像像素值变化平坦的地方其梯度的模较小，使得锐化后的图像偏暗。
（2）阈值判断：设定一个阈值，判断点的梯度的模与阈值的大小关系，根据一定的法则对锐华输出进行选择，如：

这种方法既可以保留原图背景，又可对图像进行一定程度的锐化。
（3）为背景设定一个特定的像素值：这种方法与（2）相似，主要是为了更多得保存背景信息：

（4）为边缘设定一个特定的像素值：与（3）相反，主要是为了更多得保留边缘信息：

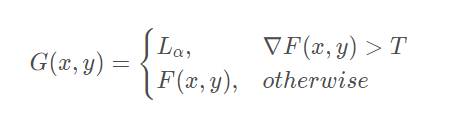
（5）二值化：与图像二值化类似：

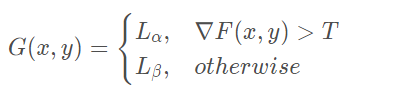
2.Robert算子法

Robert算子无方向性，采用对角之间的差分法代替上文提到的梯度：

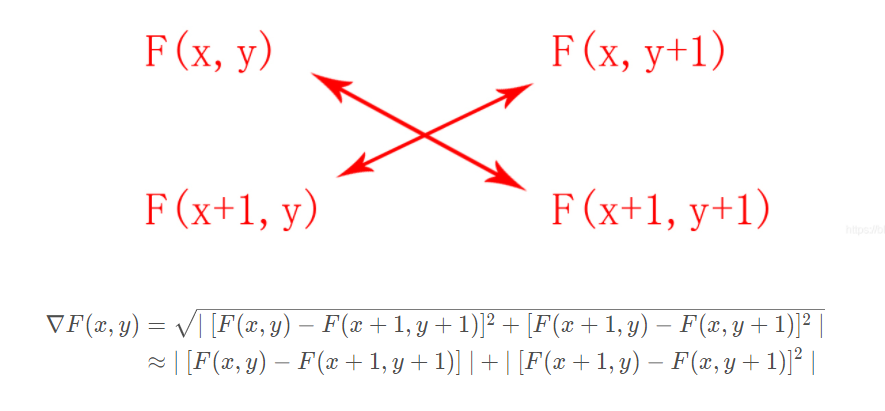
本质上也是梯度或其导出值代替像素值的思想。

3.Laplacian算子法

Laplacian算子二阶微分算子，具有旋转不变性，因此可以处理不同方向的图像锐化要求：
Laplacian算子：

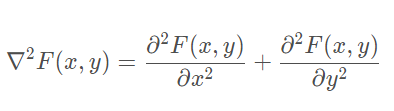
还有离散形式：

即Laplacian算子可表示为4倍的中心像素值与邻域内其他像素值之和的差值，也可表示为

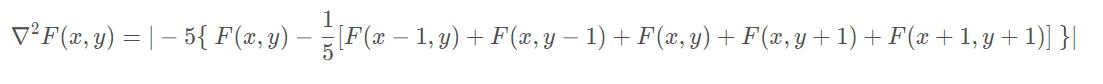
即为中心点像素值与邻域内所有像素值的均值的差值的-5倍，并求该值的绝对值，依此可以得出变形的Laplacian算子：

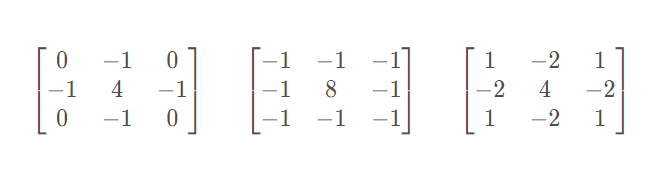
根据这几个算子可以避免微分计算。

4.高通滤波算法

高通滤波算法采用一个滤波器，抑制低频的像素值，达到锐化的目的，滤波器的工作原理是基于图像卷积操作的工作原理，对应关系为：

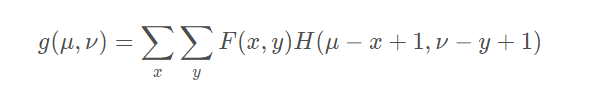
其中的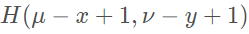被称为冲激响应，常见的有五种矩阵：

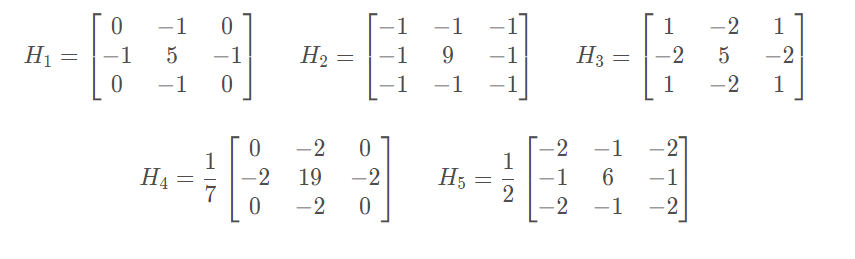
5.模板匹配法

模板匹配也是利用了图像卷积的原理，并结合了模板匹配相似性计算的思想。简单来说，在图像锐化中，使用了算子（可以理解为卷积核）与邻域内的像素值相乘，得出的值代替原有的邻域，下面介绍两种比较常见的算子：
Prewitt算子：
Prewitt算子有八个方向，对应了八个算子：

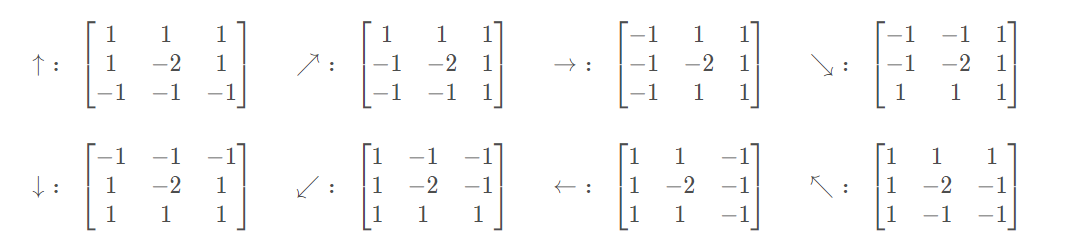
Sobel算子：
Sobel算子是对Prewitt算子的改进，将八个方向简化成两个轴。
Sobel算子有两个轴，一个x轴一个y轴，故其由两个算子组成，为：


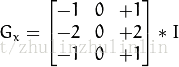
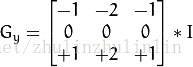
具体计算方法如下：

由于篇幅原因，代码示例将在下一篇介绍