二叉树

树(Tree)

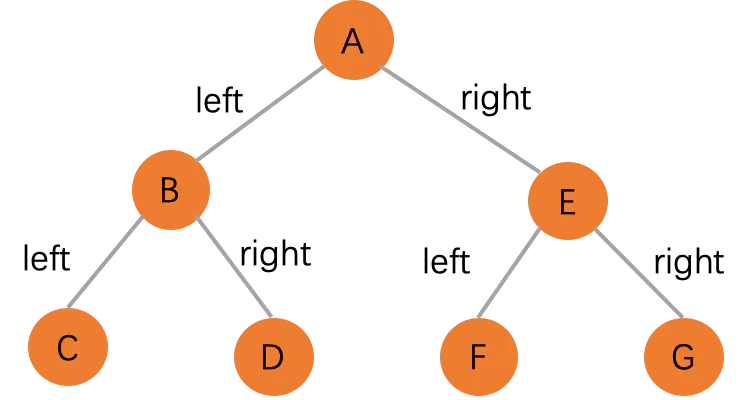
树是计算机中经常用到的一种数据结构，与列表不同，它是一种非线性的数据结构，以分层的方式来储存数据。像公司的组织架构，就可以理解成一棵树。

一棵树最上面的节点被称为根节点，在下图中，A 就是根节点。如果一个节点下面连接多个节点，该节点被称为父节点，它下面的节点被成为子节点，一个节点可以有0、1或多个子节点，没有子节点的节点被称为叶子节点。A 是 B 的父节点，B 是 A 的子节点。C 和 D 属于同一个父节点 B，他们直接互相称之为兄弟，即互相为兄弟节点。C、D、F、H 和 I 都是叶子节点。

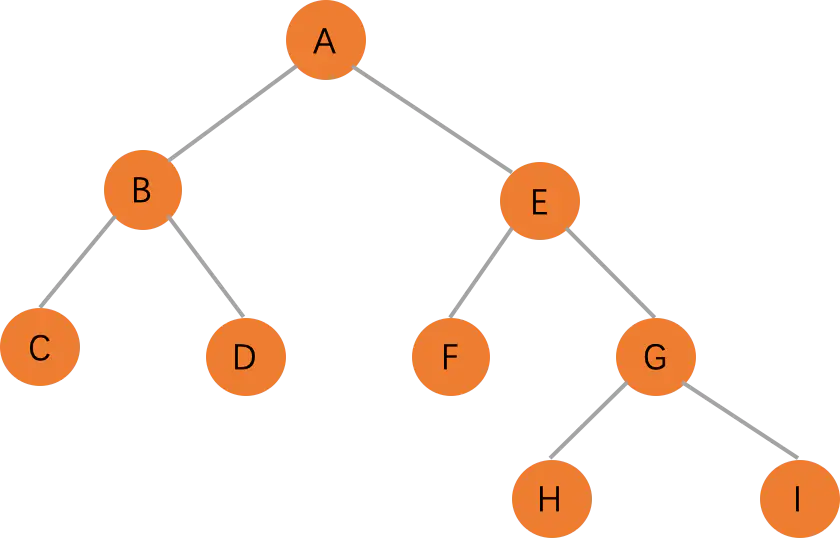
二叉树(Binary Tree)

二叉树是一种特殊的树，它的子节点个数不超过两个。上面的图就是一个二叉树。

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为 kk ，且结点总数是2^k - 12k−1，则它就是满二叉树。[来自百度百科]。

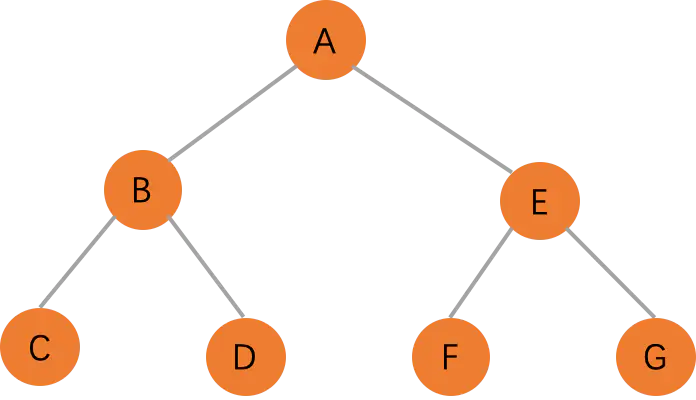
满二叉树(Full Binary Tree)

我们发现，满二叉树的所有叶子节点都在最底层，而且除了叶子节点，其他的节点都有左右两个子节点。

看完满二叉树，来认识一下由其引出来的完全二叉树，可能光看字面意思不是很好理解。若设二叉树的深度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

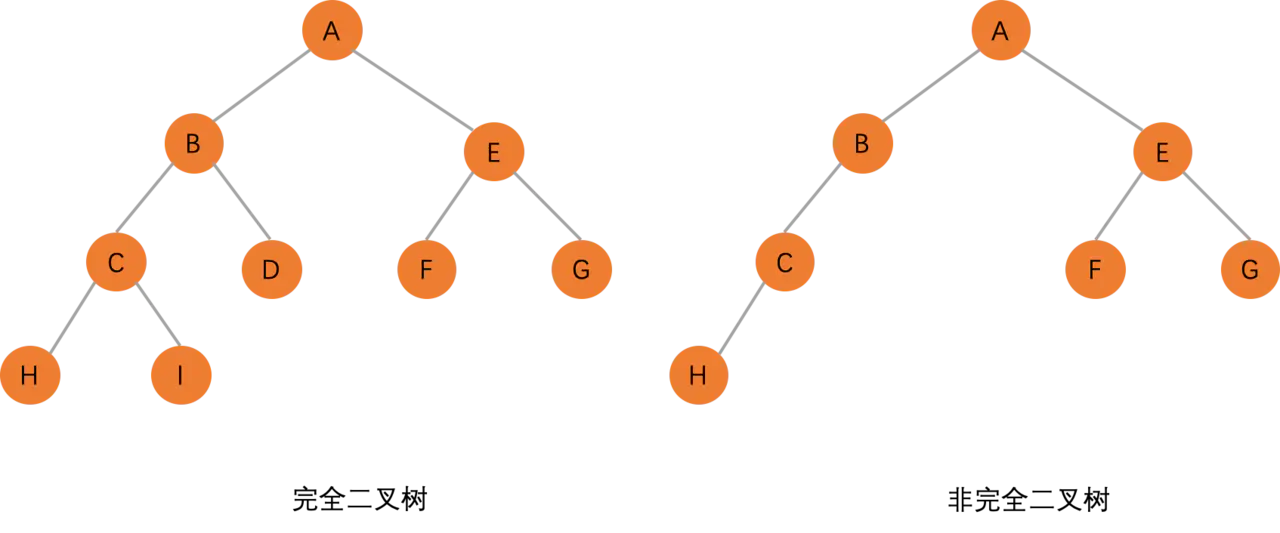
对于大多数同学来说 ，满二叉树很好理解，但是到了完全二叉树可能就迷糊了，下面的图给出了几个完全二叉树和非完全二叉树的例子，相信你看了应该就明白是怎么回事了。

二叉树的存储结构

存储一棵二叉树，有两种方法，一种是基于指针或者引用的二叉链式存储，一种是基于数组的顺序存储。

先来看大家都比较熟悉、更加直观的链式存储结构。链式存储结构中，每一个结点包含三个关键属性：指向左子节点的指针，数据，指向右子节点的指针。

• 结构定义

class Node {
  public data: any;
  public left?: Node;
  public right?: Node;
  constructor({ data, left, right }) {
    this.data = data;
    this.left = left;
    this.right = right;
  }
}

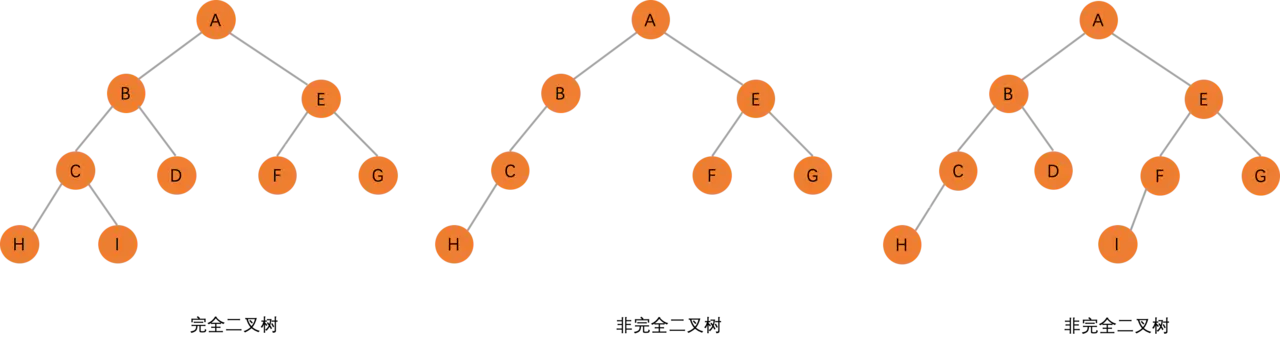
再来看基于数组的顺序存储，为了帮助大家更好地理解，这里拿了一张完全二叉树的图。使用顺序存储，完全二叉树是非常合适的，可以自上而下，从左到右来顺序存储 n 个结点的完全二叉树。

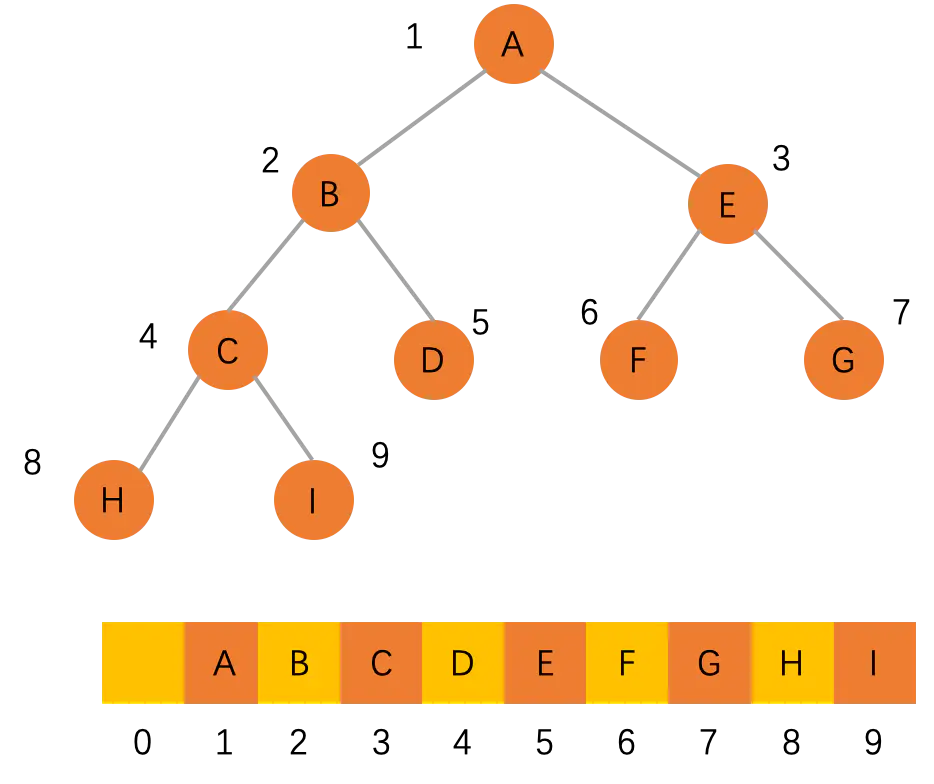
我们把根节点放到 i = 1i=1，那么根节点的左子节点存储在下标 2 * i = 22∗i=2 的位置，右子节点存储在 2 * i + 1 = 32∗i+1=3 的位置。依此类推，B 节点的左子节点存储在 2 * i = 2 * 2 = 42∗i=2∗2=4 的位置，右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 52∗i+1=2∗2+1=5 的位置。

完全二叉树的这种存储结构，有以下特点：

• 非根节点的父节点对应数组下标为是 i / 2i/2
• 节点的左子节点的序号是 2 * i2∗i*,如果*2 * i > n2∗i>n，则左子节点不存在
• 节点的右子节点的序号是2 * i + 12∗i+1*，如果2 i > n + 12∗i>n+1，则右子节点不存在

如果不是完全二叉树，用这种结构来存储会浪费比较多的空间，可以看下面的图。

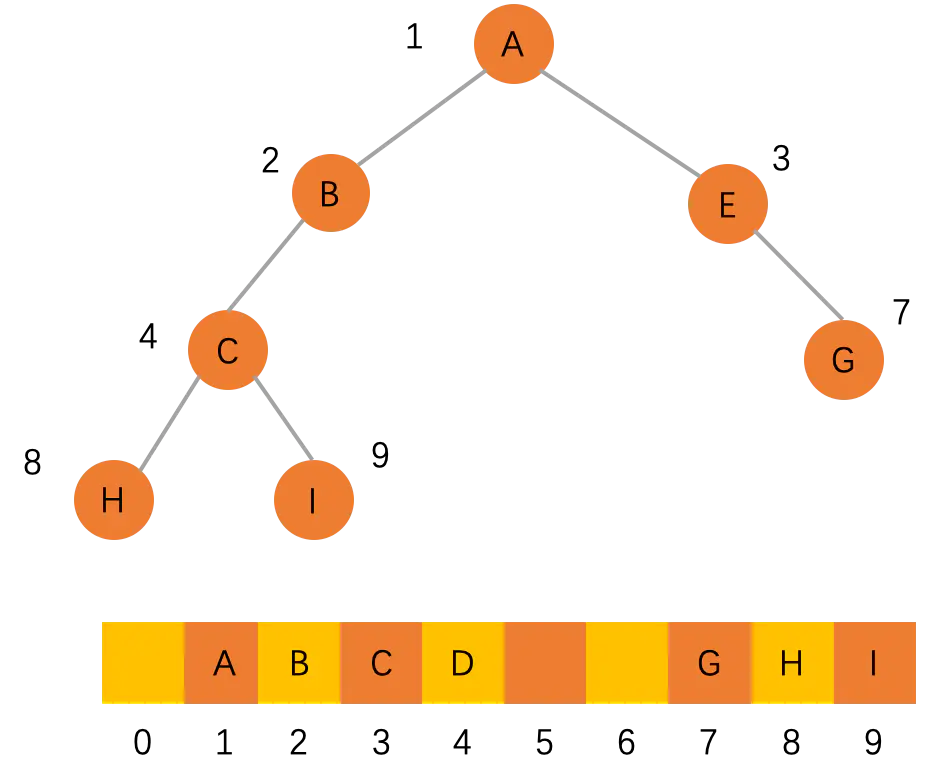
因此，如果一棵树刚好是完全二叉树，采用顺序存储是最节省内存空间的，不需要额外再提供左右两个指针。

二叉树的遍历

二叉树的常见的遍历方法有 3 种：前序遍历、中序遍历、和后序遍历，依据节点和它的左右子树的遍历顺序不同来划分。

• 前序遍历：对于二叉树中的任意节点，先访问该节点，再去访问当前节点的左子树，然后是右子树，若当前节点无左子树，则访问当前节点的右子树；
• 中序遍历：对于二叉树中的任意节点，先访问该节点的左子树，再去访问当前节点，然后是右子树；
• 后序遍历：对于二叉树中的任意节点，先访问该节点的左子树，再去访问当前节点的右子树，然后是当前节点；

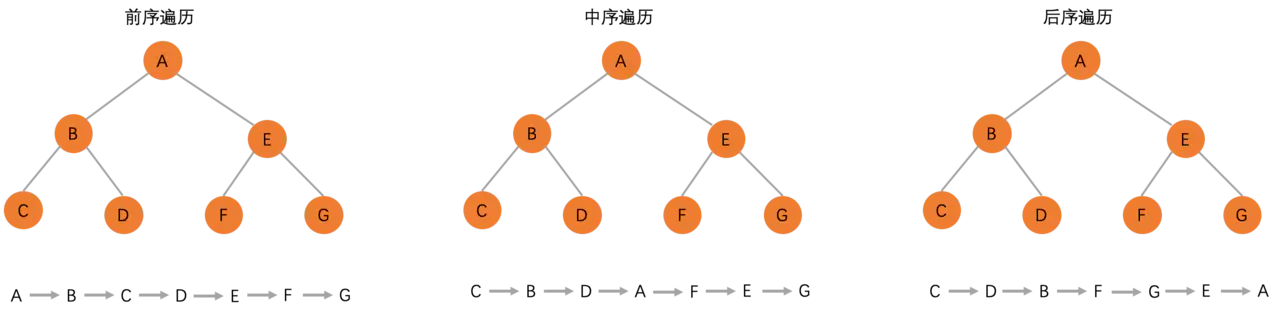
二叉树是一种递归形式的数据结构，因此对于二叉树的 3 种遍历，我们就可以借助其自身的特性，通过递归实现。

// 前序遍历
function preTraversal(node) {
  if (node === null) {
    return;
  }
  console.log(node.data);
  preTraversal(node.left);
  preTraversal(node.right);
}

// 中序遍历
function inTraversal(node) {
  if (node === null) {
    return;
  }
  inTraversal(node.left);
  console.log(node.data);
  inTraversal(node.right);
}

// 后序遍历
function postTraversal(node) {
  if (node === null) {
    return;
  }
  postTraversal(node.left);
  postTraversal(node.right);
  console.log(node.data);
}

可以看到，使用递归实现二叉树的遍历十分简单。

二叉查找树(Binary Search Tree)

二叉查找树(BST)是一种特殊的二叉树，较小的值保存在左子树中，较大的值保存在右子树中，这一特性使得 查找的效率很高。因此它又有另外一个名字，叫二叉排序树(Binary Sort Tree)。看了图是不是瞬间明白二叉查找树是个啥。

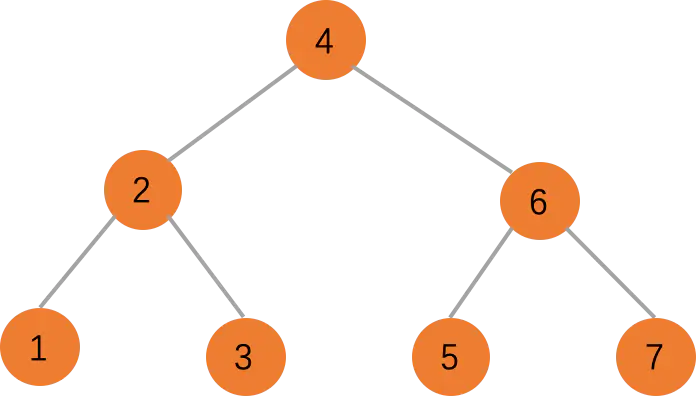
二叉查找树的查找

对于 BST 通常有以下 3 种类型的查找：

• 找给定值
• 找最小值
• 找最大值

根据二叉查找树的属性，查找最小值和最大值比较简单。因为较小的值总是在左子节点上，要找到最小值，只需要遍历左子树，直到找到最后一个节点。

function getMin() {
  let currentNode = this.tree;
  while (currentNode.left !== null) {
    currentNode = currentNode.left;
  }
  return currentNode.data;
}

查找最大值也是同理，只需遍历右子树，直到找到最后一个节点即可。

function getMax() {
  let currentNode = this.tree;
  while (currentNode.right !== null) {
    currentNode = currentNode.right;
  }
  return currentNode.data;
}

在 BST 上查找给定值，通过比较该值和当前节点上的值的大小，就能够确定向左还是向右遍历。

function find(data) {
  let node = this.tree;
  while (node !== null) {
    if (node.data === data) {
      return node;
    } else if (data < node.data) {
      node = node.left;
    } else {
      node = node.right;
    }
  }
}

二叉查找树的插入

在二叉查找树中插入元素比较复杂，分为以下几种情况：

• 首先需要检查 BST 是否有根节点，如果没有，插入的节点就是根节点，就完事了
• 如果待插入的节点不是根节点，那么就需要遍历整棵树，找到合适的位置

如果要插入的数据大于当前节点，并且当前节点的右子树为空，就将新数据插入到右子节点的位置；如果不为空，就再递归遍历右子树，查找插入位置。同理，如果要插入的数据小于当前节点，并且节点的左子树为空，就将新数据插入到左子节点的位置；如果不为空，就再递归遍历左子树，查找插入位置。

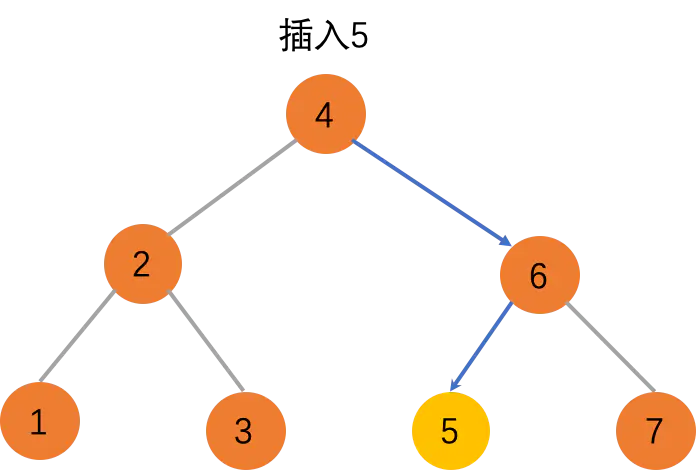
function insert(data) {
  const n = new Node(data);
  if (this.tree === null) {
    this.tree = n;
    return;
  }

  let node = this.tree;
  while (node !== null) {
    if (data > node.data) {
      if (node.right === null) {
        node.right = n;
        return;
      }
      node = node.right;
    } else {
      if (data < node.data) {
        if (ndoe.left === null) {
          node.left = n;
          return;
        }
        node = node.left;
      }
    }
  }

}

二叉查找树的删除

在二叉查找树上删除节点的操作最复杂，牵一发而动全身，节点直接存在相互关联。如果删除的是没有子节点的节点，那就直接删掉就完事了。稍微麻烦的是删除节点只有一个子节点的情况，如果删除的节点包含两个子节点，那就是最麻烦的了。

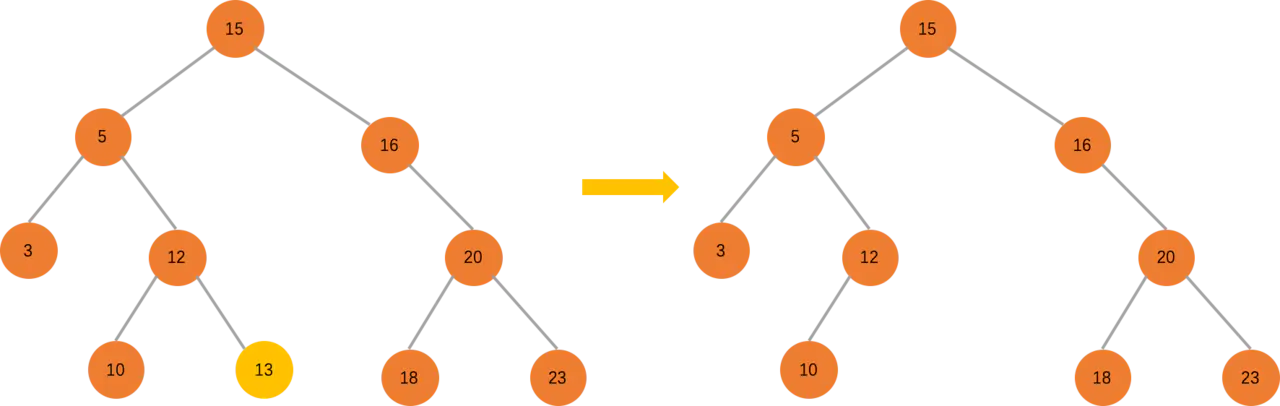
删除没有子节点的节点

如果没有子节点，直接把要删除的节点干掉就行

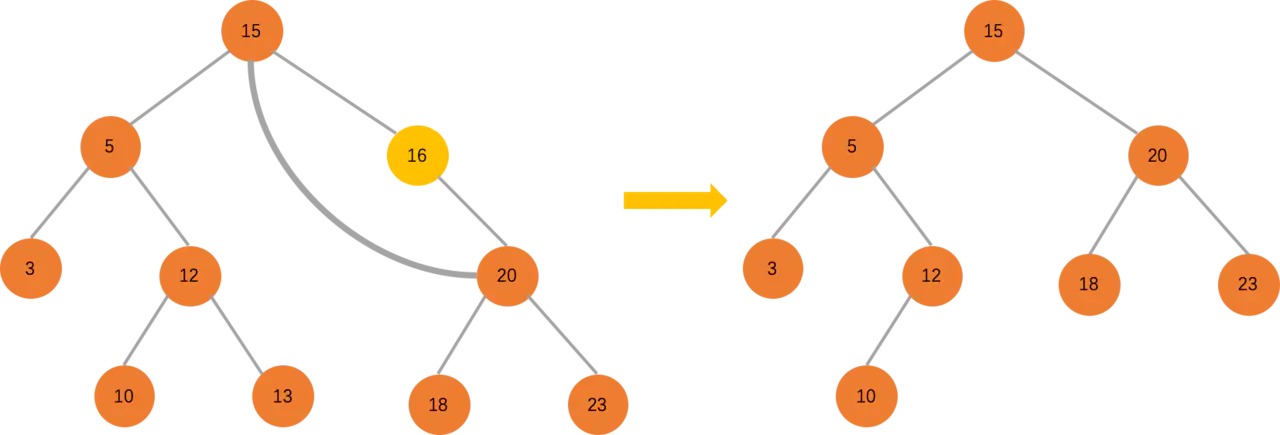
删除只有一个子节点的节点

只有一个子节点只需要把更新父节点指向要删除节点的指针，指向要删除节点的子节点就可以了。比如图中删除节点的节点是 16，把 15 指向 13 的指针指向 20 即可。

现在来看最复杂的情况：

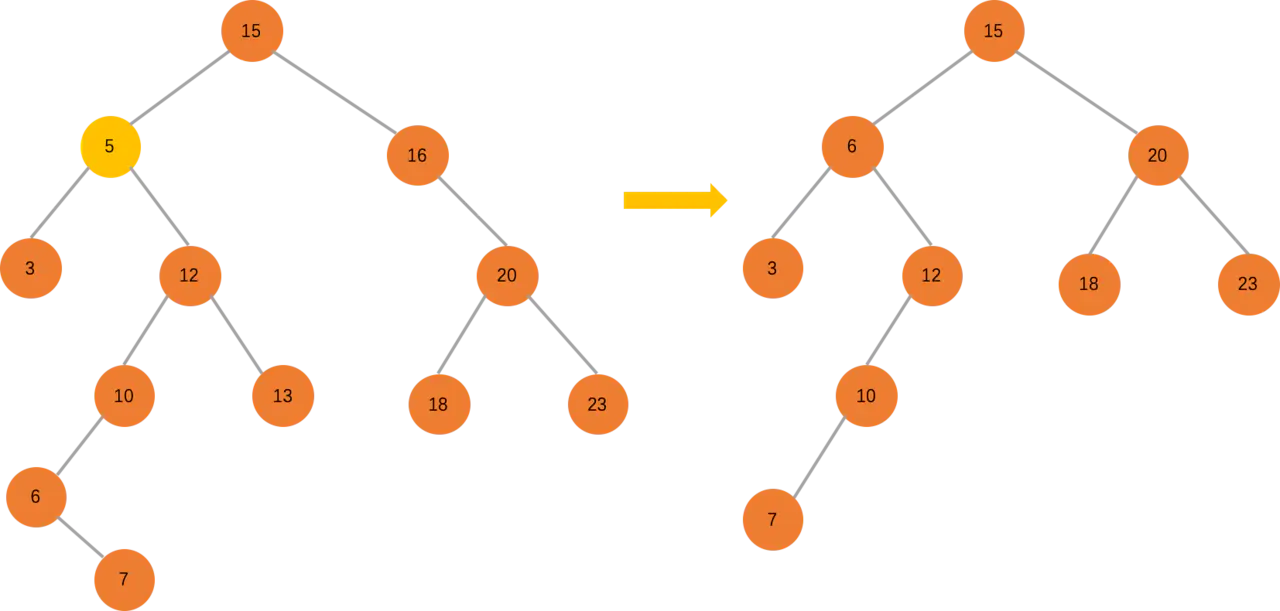
删除有两个子节点的节点

有两个子节点，我们需要查找右子树上的最小值，把它拿到待删除的节点上，然后再删除这个最小的节点。删除这个最小的节点，又回到了上面讲的两条规则，这个最小节点不可能有两个子节点，如果有左子节点，就不是最小节点了。

function remove(data) {
  let node = this.tree;
  let parentNode;
  while (node !== null && node.data != data) {
    parentNode = node;
    if (data > node.data) {
      node = node.right;
    } else {
      node = node.left;
    }
  }

  if (node === null) {
    return; // 没找着
  }

  // 我们采用非递归的方式，先处理要删除的节点有两个子节点的情况
  if (node.left !== null && node.right !== null) {
    // 查找右子树中最小节点
    let minNodeParent = node;
    let minNode = minNodeParent.right;
    while (minNodeParent.left !== null) {
      minNodeParent = minNode;
      minNode = minNode.left;
    }
    node.data = minNode.data;
    node = minNode; // 下面就变成删除 minNode 了
    parentNode = minNodeParent;
  }

  // 删除节点是叶子节点或者只有一个子节点
  let childNode = null;
  if (node.left !== null) {
    childNode = node.left;
  } else if (node.right !== null) {
    childNode = node.right;
  }

  if (parentNode === null) { // 父节点是 null，说明删除的是根节点
    this.tree = childNode;
  // 第二种情况，把父节点的指向删除节点的指针指向删除节点的子节点
  // 删除的是 node，把 parentNode 指向 node 的指针，指向 childNode
  } else if (parentNode.left === node) {
    parentNode.left = childNode;
  } else {
    parentNode.right = childNode;
  }
}

本章节分为 4 个部分：

• Part 1
  • 最小栈
  • Shuffle an Array
  • 将有序数组转换为二叉搜索树
• Part 2
  • 对称二叉树
  • 二叉树的最大深度
  • 验证二叉搜索树
• Part 3
  • 二叉树的层次遍历
  • 二叉树的序列化与反序列化
• Part 4
  • 中序遍历二叉树
  • 从前序与中序遍历序列构造二叉树
  • 二叉搜索树中第 K 小的元素
• Part 5
  • 填充每个节点的下一个右侧节点指针
  • 岛屿数量
  • 二叉树的锯齿形层次遍历

阅读完本章节，你将有以下收获：

• 熟悉栈的数据结构，可以解决基本栈相关问题
• 掌握二叉树的概念
• 会用不同的方法去遍历二叉树，解决相关问题

最小栈、Shuffle an Array和将有序数组转换为二叉搜索树

最小栈

设计一个支持 push，pop，top 操作，并能在常数时间内检索到最小元素的栈。

• push(x) – 将元素 x 推入栈中。
• pop() – 删除栈顶的元素。
• top() – 获取栈顶元素。
• getMin() – 检索栈中的最小元素。

示例

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

方法一 最小元素栈

思路

根据数组的性质，push、pop、top都能在常数时间内完成，而此题关键是常数时间内检索最小元素，此解法是开辟一个数组存储，push数据同时，存储当前栈中最小元素，pop数据的同时pop最小元素栈栈顶数据；

详解

1. 创建最小元素栈时，开辟 stack 及 minStack 数组，stack 用于存储压栈元素，minStack 用于存储最小元素序列；
2. push操作执行元素 x 压栈：
3. 如果 minStack 数组为空时，添加元素 x 到 minStack 数组。
4. 否则比较元素 x 与数组末尾元素，取最小值添加到 minStack 数组末尾。表示当前栈中元素的最小值为x。
5. pop操作:
6. 删除 stack 数组末尾元素的同时，删除数组 minStack 末尾元素。
7. getMin操作:
8. 直接调用 pop 方法，返回 minStack 数据中末尾元素即可。

const MinStack = function () {
  this.stack = [];
  this.minStack = [];
};

/**
 * @param {number} x
 * @return {void}
 */
MinStack.prototype.push = function (x) {
  this.stack.push(x);
  if (this.minStack.length === 0) {
    this.minStack.push(x);
  } else {
    const min = Math.min(this.minStack[this.minStack.length - 1], x);
    this.minStack.push(min);
  }
};

/**
 * @return {void}
 */
MinStack.prototype.pop = function () {
  this.minStack.pop();
  return this.stack.pop();
};

/**
 * @return {number}
 */
MinStack.prototype.top = function () {
  return this.stack[this.stack.length - 1];
};

/**
 * @return {number}
 */
MinStack.prototype.getMin = function () {
  return this.minStack[this.minStack.length - 1];
};

复杂度分析

• 时间复杂度：O(1)O(1)

  push、pop、top、getMin 操作都是基于数组索引，耗费 O(1) 的时间。

• 空间复杂度：O(n)O(n)

  每次 push 一个元素到 stack 栈的同时将 stack 栈中最小元素 push 到 minStack 栈，耗费O(n)O(n)的栈空间

方法二 差值存储

思路

用一个min变量保存最小值，每次push操作压栈时,保存的是入栈的值和最小值min的差值，而不是入栈的值；pop出栈时，通过min值和栈顶的值得到；不过此算法有一个缺陷，两数差值有溢出风险。

详解

1. 创建最小元素栈时，开辟 stack 数组，用于存储入栈元素x与最小元素 min 的差值；同时定义变量 min，用于存储最小值，初始值为 Number.MAX_VALUE。
2. push 操作执行元素x入栈：：
3. 取元素 x 与最小元素 min 的差值，压入stack数组：
4. 比较元素x与min值，取其最小值赋值给min变量。
5. pop操作:
6. 弹出stack数组末尾元素值 value，如果值value > 0，说明push操作的值大于 min，返回 value + min 值；如果值value <= 0，说明 push 操作的值小于等于原 min 值，恢复最小值min，同时返回 min 值即可。
7. top 操作:
8. 取stack数组末尾元素值 value，如果值 value > 0，说明push操作的值大于min，返回 value + min 值；如果值 value <= 0，说明 push 操作的值小于等于原 min 值，返回 min 值即可。
9. getMin 操作:
10. 返回 min 元素即可。

const MinStack = function () {
  this.stack = [];
  this.min = Number.MAX_VALUE;
};

/**
 * @param {number} x
 * @return {void}
 */
MinStack.prototype.push = function (x) {
  const min = this.min;
  this.stack.push(x - min);
  if (x < min) {
    this.min = x;
  }
};

/**
 * @return {void}
 */
MinStack.prototype.pop = function () {
  const value = this.stack.pop();
  const min = this.min;
  if (value > 0) {
    return value + min;
  } else {
    this.min = min - value;
    return min;
  }
};

/**
 * @return {number}
 */
MinStack.prototype.top = function () {
  const value = this.stack[this.stack.length - 1];
  if (value > 0) {
    return value + this.min;
  } else {
    return this.min;
  }
};

/**
 * @return {number}
 */
MinStack.prototype.getMin = function () {
  return this.min;
};

复杂度分析

• 时间复杂度：O(1)O(1)

• 空间复杂度：O(1)O(1)

  每次 push 一个元素到 stack 栈的同时只需要一个元素空间存储最小值，耗费O(1)O(1)的栈空间

Shuffle an Array

打乱一个没有重复元素的数组。

示例

// 以数字集合 1, 2 和 3 初始化数组。

int[] nums = {1,2,3};

Solution solution = new Solution(nums);

// 打乱数组 [1,2,3] 并返回结果。任何 [1,2,3]的排列返回的概率应该相同。

solution.shuffle();

// 重设数组到它的初始状态[1,2,3]。

solution.reset();

// 随机返回数组[1,2,3]打乱后的结果。

solution.shuffle();

方法一

思路

• reset 函数：缓存传入的原始数据，用于在函数调用时返回。但值得一提的是，进行缓存原始数据时，必须进行浅拷贝，因为原始数据为数组，普通的赋值会导致引用对象传递，一旦变更了 this.nums 的数组内容，缓存的数组也将同步变更
• shuffle` 函数：我们模拟一个这样的场景，有 n 个标着数的球，我们把这 n 个球放入一个看不见的袋子中，每次从中摸一个球出来，并按照摸出的顺序，直到摸空袋子。具体的操作，我们把原始数组复制一份为 nums，每次根据 nums 的长度随机生成一个下标从 nums 中取一个数出来，将其放入新数组 ary 中，并删除 nums 中对应下标的数

详解

1. 定义 this.nums 存储传入的数据
2. 定义 this.original 存储 nums 的克隆数组
3. 定义重置 reset 方法，将 this.nums 重制为 this.original 的克隆数组，并将 this.original 重新克隆一遍（因数组为引用对象，不重新缓存新数组会导致 this.original 和 this.nums 同步变化）
4. 定义打乱 shuffle 方法，根据 this.nums 的长度进行循环，每次从根据 this.nums 长度通过 Math.random() 随机生成一个下标
5. 根据随机生成的下标，将值存入 ary 数组中
6. 最后返回 ary 数组

代码

/**
 * @param {number[]} nums
 */
const Solution = (nums) => {
  this.nums = nums;
  this.original = nums.slice(0);
};
/**
 * 重置数组并返回
 * @return {number[]}
 */
Solution.prototype.reset = () => {
  this.nums = this.original;
  this.original = this.original.slice(0);
  return this.original;
};
/**
 * 返回一个随机重排的数组
 * @return {number[]}
 */
Solution.prototype.shuffle = () => {
  const ary = [];
  const nums = this.nums.slice(0);
  const len = nums.length;
  for (let i = 0; i < len; i += 1) {
    const targetIndex = Math.floor(Math.random() * nums.length);
    ary[i] = nums[targetIndex];
    nums.splice(targetIndex, 1);
  }
  return ary;
};

复杂度分析

• 时间复杂度：O(n^2)O(n2)

  js 中 splice 方法的时间复杂度为 O(n)O(n)，因为当你在中间删除一个元素后，在此位置之后的所有元素都需要整体向前移动一个位置，因此导致遍历所有 nn 个元素，又因为 splice 方法于 for 循环中需执行 nn 遍，因此为 O(n^2)O(n2)。

• 空间复杂度：O(n)O(n)

  为实现重置功能，原始数组需保存一份，因此为 O(n)O(n)。

方法二

思路

• reset 函数：同方法一
• shuffle 函数：为降低方法一中的时间复杂度，我们可以让数组中的元素进行互换，从而减少 splice 方法所需执行的时间。具体的操作，我们从数组的最后往前迭代，生成一个范围在 0 到当前遍历下标之间的随机整数，和当前遍历下标的元素进行互换。这跟方法一中的模拟摸球是一样的，每次被摸出的球便不能再被摸出来。

详解

1. 定义 this.nums 存储传入的数据
2. 定义 this.original 存储 nums 的克隆数组
3. 定义重置 reset 方法，将 this.nums 重制为 this.original 的克隆数组，并将 this.original 重新克隆一遍（因数组为引用对象，不重新缓存新数组会导致 this.original 和 this.nums 同步变化）
4. 定义打乱 shuffle 方法，根据 this.nums 的长度进行倒序循环，每次从根据当前下标 i 通过 Math.floor(Math.random() * (i + 1)) 随机生成一个下标（Knuth-Durstenfeld Shuffle算法）
5. 根据随机生成的下标，和当前下标，进行数据互换
6. 最后返回 nums 数组

代码

/**
 * @param {number[]} nums
 */
const Solution = (nums) => {
  this.nums = nums;
  this.original = nums.slice(0);
};
/**
 * 重置数组并返回
 * @return {number[]}
 */
Solution.prototype.reset = () => {
  this.nums = this.original;
  this.original = this.original.slice(0);
  return this.original;
};
/**
 * 返回一个随机重排的数组
 * @return {number[]}
 */
Solution.prototype.shuffle = () => {
  const nums = this.nums.slice(0);
  const len = nums.length;
  for (let i = len - 1; i > 0; i -= 1) {
    const targetIndex = Math.floor(Math.random() * (i + 1));
    const tmp = nums[i];
    nums[i] = nums[targetIndex];
    nums[targetIndex] = tmp;
  }
  return nums;
};

复杂度分析

• 时间复杂度：O(n)O(n)

  上述算法中，for 循环内操作都是常数时间复杂度，因此为 O(n)O(n)。

• 空间复杂度：O(n)O(n)

  为实现重置功能，原始数组需保存一份，因此为 O(n)O(n)。