一、矩阵

1、定义矩阵

定义矩阵 : 行之间的元素使用 空格 或 逗号隔开 , 每行之间使用分号隔开 ;

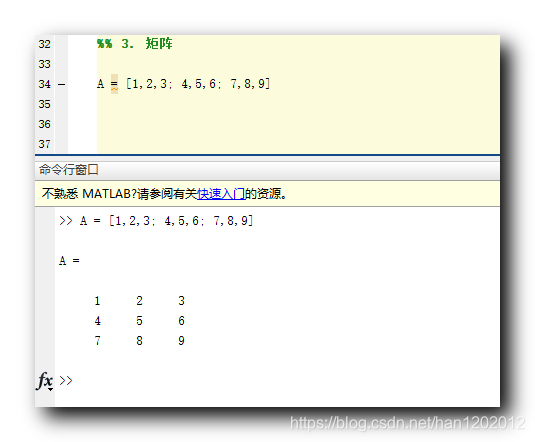
% 定义矩阵
A = [1,2,3; 4,5,6; 7,8,9]

  

 

  
1
  
2
 

执行效果 :

2、转置矩阵

转置矩阵 : 在矩阵变量右侧添加一个单引号 , 就是该矩阵的转置矩阵 ;

% 定义矩阵 B , 矩阵值是 A 的转置矩阵 
B = A'

  

 

  
1
  
2
 

执行效果 :

3、矩阵放到一列

将矩阵放到一列中 :

% 将矩阵按照列放到一列中 , 依次是第一列,第二列 ...
C = A(:)

  

 

  
1
  
2
 

执行效果 :

4、逆矩阵

逆矩阵 : 注意只有方阵才能求逆矩阵 , 否则报错 ;

% 逆矩阵, 只有方阵才能求逆矩阵
D = inv(A)

  

 

  
1
  
2
 

执行结果 :

二、随机数函数

1、rand 随机数函数

rand 随机数函数 :

作用 : 生成分布在 0 ~ 1 之间的均匀分布的伪随机数 ;

语法 :

• rand(m, n) , 生成 m 行 , n 列 , 均匀分布的伪随机数 ;
• rand(m, n, 'double') 生成指定精度的 , m 行 , n 列 , 均匀分布的伪随机数 ;
• rand(RandStream, m, n) 使用 RandStream 作为随机种子 , 生成 m 行 , n 列 , 均匀分布的伪随机数 ;

2、randn 随机数函数

randn 随机数函数 :

作用 : 生成 标准正态分布的 伪随机数 ; 标准正态分布指的是均值 $0$ , 方差 $1$ ;

语法 :

• randn(m, n) , 生成 m 行 , n 列 , 标准正态分布的伪随机数 ;
• randn(m, n, 'double') 生成指定精度的 , m 行 , n 列 , 标准正态分布的伪随机数 ;
• randn(RandStream, m, n) 使用 RandStream 作为随机种子 , 生成 m 行 , n 列 , 标准正态分布的伪随机数 ;

3、randi 随机数函数

randi 随机数函数 :

作用 : 生成 均匀分布 的伪随机整数 ;

语法 :

• rand(iMax) , 生成 ( 0 , iMax ) 开区间内 , 均匀分布 的伪随机整数 ;
• rand(iMax, m, n) , 生成 ( 0 , iMax ) 开区间内 , m 行 , n 列 , 均匀分布 的伪随机整数 ;
• rand([iMin, iMax], m, n) , 生成 ( iMin , iMax ) 开区间内 , m 行 , n 列 , 均匀分布 的伪随机整数 ;

三、生成矩阵

1、生成 0 矩阵

使用 zeros 函数生成 0 矩阵 ;

% 生成 0 矩阵 , 最后一个 3 代表 3 维矩阵
% 开始的 3 和 2 分别代表 3 行 2 列
E = zeros(3, 2, 3)

  

 

  
1
  
2
  
3
 

执行结果 :

2、生成随机矩阵

使用 rand , randi , randn 生成不同分布 , 不同取值类型 , 不同区间的随机矩阵 ;

% 生成 0 矩阵 , 最后一个 3 代表 3 维矩阵
% 开始的 3 和 2 分别代表 3 行 2 列
E = zeros(3, 2, 3)

% 随机生成均匀分布的随机数, 0 ~ 1 区间中 
E(:,:,1) = rand(3, 2)

% 随机生成均匀分布的随机整数, 0 ~ 20 开区间中 
E(:,:,2) = randi(20, 3, 2)

% 随机生成正太分布的随机数, 0 ~ 1 区间中 
E(:,:,3) = randn(3, 2)

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
 

执行结果 :

文章来源: hanshuliang.blog.csdn.net，作者：韩曙亮，版权归原作者所有，如需转载，请联系作者。

原文链接：hanshuliang.blog.csdn.net/article/details/115718713