👉🏻上一篇：❤️四万字《画解动态规划》从入门到精通（上）❤️

---

四、记忆化搜索

  给定一个 $n(n \le 45)$，求 斐波那契数列的第 $n$ 项的值，要求用递归实现。

  那么，我们只需要套用上面的递归函数，并且处理好递归出口，就能把它写成递归的形式，C语言 代码实现如下：

int f(unsigned int n) {
    if(n <= 1) {
        return 1;
    }
    return f(n-1) + f(n-2);
}

  递归求解的过程如下：

  这是一棵二叉树，树的高度为 $n$，所以粗看递归访问时结点数为 $2^n$，但是仔细看，对于任何一棵子树而言，左子树的高度一定比右子树的高度大，所以不是一棵严格的完全二叉树。为了探究它实际的时间复杂度，我们改下代码：

int f(unsigned int n) {
    ++c[n];
    if(n <= 1) {
        return 1;
    }
    return f(n-1) + f(n-2);
}

  加了一句代码 ++c[n];，引入一个计数器，来看下在不同的 $n$ 的情况下， $f(n)$ 这个函数的调用次数，如图所示：

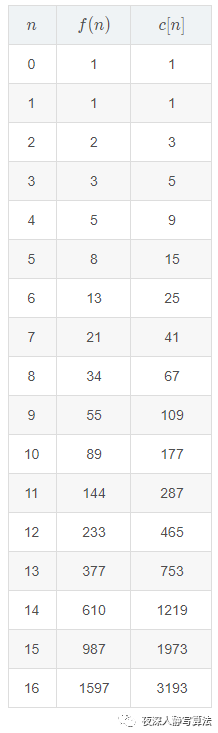
  观察 $c[n]$ 的增长趋势，首先排除等差数列，然后再来看是否符合等比数列，我们来尝试求下 $c[n] / c[n-1]$ 的值，列出表格如下：

  观察发现，随着 $n$ 的不断增大， $c[n]/c[n-1]$ 越来越接近一个常数，而这个常数就是黄金分割的倒数：

$$\frac {2}{ \sqrt 5 - 1} \approx 1.618034$$

  当 $n$ 趋近于无穷大的时候，满足如下公式：

$$c[n] = \frac {2}{ \sqrt 5 - 1} c[n-1]$$

  对等比数列化解后累乘得到：

$$\begin{aligned}c[n] &= \frac {2}{ \sqrt 5 - 1} c[n-1]\\ &= (\frac {2}{ \sqrt 5 - 1})^2 c[n-2]\\ &= (\frac {2}{ \sqrt 5 - 1})^n \end{aligned}$$

  所以，斐波那契数列递归求解的时间复杂度就是 ：

$$O((\frac {2}{ \sqrt 5 - 1})^n)$$

  这是一个指数级的算法，随着 $n$ 的不断增大，时间消耗呈指数级增长，我们在写代码的时候肯定是要避免这样的写法的，尤其是在服务器开发过程中，CPU 是一种极其宝贵的资源，任何的浪费都是可耻的。但是，面试官又要求用递归实现，真是太讨厌了！
  那么，怎么来优化这里的算力消耗呢？
  递归求解斐波那契数列其实是一个深度优先搜索的过程，它是毫无优化的暴力枚举，对于 $f(5)$ 的求解，如图所示：

  同时，我们也发现，计算过程中其实有很多重叠子问题，例如 $f(3)$ 被计算了 $2$ 次，如图所示：

   $f(2)$ 被计算了 $3$ 次，如图所示：

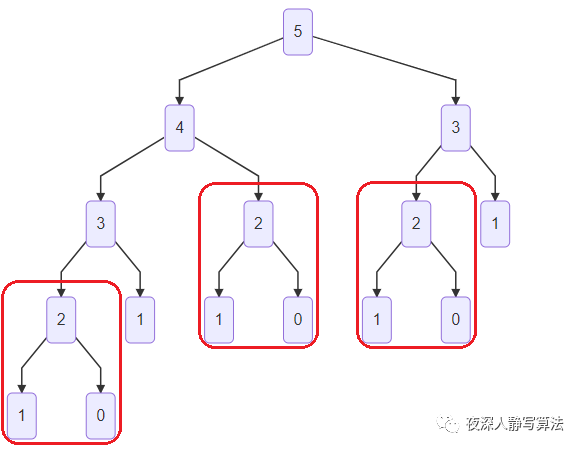
  所以如果我们能够确保每个 $f(i)$ 只被计算一次，问题就迎刃而解了。可以考虑将 $f(i)$ 计算出来的值存储到哈希数组 $h[i]$ 中，当第二次要访问 $f(i)$ 时，直接取 $h[i]$ 的值即可，这样每次计算 $f(i)$ 的时间复杂度变成了 $O(1)$，总共需要计算 $f(2),f(3),...f(n)$，总的时间复杂度就变成了 $O(n)$ 。
  这种用哈希数组来记录运算结果，避免重复运算的方法就是记忆化搜索。
  这件事情如何执行下去呢？
  我们用一个数组 $h[i]$ 来记录 斐波那契数列 第 $i$ 项的值，把之前的递归代码改成如下形式：

const int inf = -1;
int h[46];

void init() {
    memset(h, inf, sizeof(h));  // 1）
}

int f(unsigned int n) {
    if(n <= 1) {
        return 1;
    }
    int &fib = h[n];            // 2）
    if(fib != inf) {
        return fib;             // 3）
    }
    fib = f(n-1) + f(n-2);      // 4）
    return fib;
}

• 1）初始化所有 $f(i)$ 都没有被计算过，为了方便用 memset，可以将 inf定义成 -1；
• 2）注意这里用了个引用，而且一定要用引用，具体原因留给读者自己思考，当然不想思考的话，下文也会讲到，不必担心；
• 3）当 fib也就是 h[n]已经计算过了，那么直接返回结果即可；
• 4）最后，利用递归计算h[n]的值，并且返回结果；

  和递归版本相比，多了这么一段代码：

    int &fib = h[n];
    if(fib != inf) {
        return fib;
    }

  那么它的作用体现在哪里呢？我们通过一个动图来感受一下：

  如图所示，当第二次需要计算 $f(2)$ 和 $f(3)$ 时，由于结果已经计算出来并且存储在 $h[2]$ 和 $h[3]$ 中，所以上面这段代码的fib != inf表达式为真，直接返回，不再需要往下递归计算，这样就把原本的 “递归二叉树” 转换成了 “递归链”， 从而将原本指数级的算法变成了多项式级别。
  上文用一个简单的例子阐述了记忆化搜索的实现方式，并且提到了利用数组来记录已经计算出来的重叠子问题，这个和动态规划的思想非常相似，没错，记忆化搜索其实用的就是动态规划的思想。更加确切的说，可以用如下公式来表示：

记忆化搜索 = 深度优先搜索的实现 + 动态规划的思想
  有关记忆化搜索的更多内容，可以参考：夜深人静写算法（二十六）- 记忆化搜索。

五、背包问题

1、0/1 背包

  有 $n(n \le100)$ 个物品和一个容量为 $m(m \le 10000)$ 的背包。第 $i$ 个物品的容量是 $c[i]$，价值是 $w[i]$。现在需要选择一些物品放入背包，并且总容量不能超过背包容量，求能够达到的物品的最大总价值。

  以上就是 0/1 背包问题的完整描述，之所以叫 0/1 背包，是因为每种物品只有一个，可以选择放入背包或者不放，而 0 代表不放，1 代表放。
  第一步：设计状态；
  状态 $(i, j)$ 表示前 $i$ 个物品恰好放入容量为 $j$ 的背包 $(i \in [0, n], j \in [0, m])$；
  令 $dp[i][j]$ 表示状态 $(i, j)$ 下该背包得到的最大价值，即前 $i$ 个物品恰好放入容量为 $j$ 的背包所得到的最大总价值；
  第二步：列出状态转移方程；

$$dp[i][j] = max(dp[i-1][j], dp[i-1][j - c[i]] + w[i])$$

因为每个物品要么放，要么不放，所以只需要考虑第 $i$ 个物品 放 或 不放 的情况：
  1）不放：如果 “第 $i$ 个物品不放入容量为 $j$ 的背包”，那么问题转化成求 “前 $i-1$ 个物品放入容量为 $j$ 的背包” 的问题；由于不放，所以最大价值就等于 “前 $i-1$ 个物品放入容量为 $j$ 的背包” 的最大价值，即 $dp[i-1][j]$；
  2）放：如果 “第 $i$ 个物品放入容量为 $j$ 的背包”，那么问题转化成求 “前 $i-1$ 个物品放入容量为 $j-c[i]$ 的背包” 的问题；那么此时最大价值就等于 “前 $i-1$ 个物品放入容量为 $j-c[i]$ 的背包” 的最大价值 加上放入第 $i$ 个物品的价值，即 $dp[i-1][j - c[i]] + w[i]$；
  将以上两种情况取大者，就是我们所求的 “前 $i$ 个物品恰好放入容量为 $j$ 的背包” 的最大价值了。
  我们发现，当状态在进行转移的时候， $(i, j)$ 不是来自 $(i-1, j)$，就是来自 $(i-1, j - c[i])$，所以必然有一个初始状态，而这个初始状态就是 $(0, 0)$，含义是 “前 0 个物品放入一个背包容量为 0 的背包”，这个状态下的最大价值为 0，即 $dp[0][0] = 0$；
  那么我们再来考虑， $(0, 3)$ 是什么意思呢？它代表的是 “前 0 个物品恰好放入一个背包容量为 3 的背包”，明显这种情况是不存在的，因为 0 个物品的价值肯定是 0。所以这种状态被称为非法状态，非法状态是无法进行状态转移的，于是我们可以通过初始状态和非法状态进所有状态进行初始化。
  

$$dp[0][i] = \begin{cases} 0 & i = 0\\ inf & i > 0\end{cases}$$

  其中 $inf$ 在程序实现时，我们可以设定一个非常小的数，比如 $-1000000000$，只要保证无论如何状态转移它都不能成为最优解的候选状态。为了加深状态转移的概念，来看图二-5-1 的一个例子，每个格子代表一个状态， $(0,0)$ 代表初始状态，蓝色的格子代表已经求得的状态，灰色的格子代表非法状态，红色的格子代表当前正在进行转移的状态，图中的第 $i$ 行代表了前 $i$ 个物品对应容量的最优值，第 4 个物品的容量为 2，价值为 8，则有状态转移如下：

$$\begin{aligned} dp[4][4] &= max( dp[4-1][4], dp[4-1][4 - 2] + 8) \\ &= max( dp[3][4], dp[3][2] + 8) \end{aligned}$$

  有关 0/1 背包的更多内容，可以参考：夜深人静写算法（十四）- 0/1 背包。

2、完全背包

  有 $n(n \le 100)$ 种物品和一个容量为 $m(m \le 10000)$ 的背包。第 $i$ 种物品的容量是 $c[i]$，价值是 $w[i]$。现在需要选择一些物品放入背包，每种物品可以无限选择，并且总容量不能超过背包容量，求能够达到的物品的最大总价值。

  以上就是完全背包问题的完整描述，和 0/1 背包的区别就是每种物品可以无限选取，即文中红色字体标注的内容；
  第一步：设计状态；
  状态 $(i, j)$ 表示前 $i$ 种物品恰好放入容量为 $j$ 的背包 $(i \in [0, n], j \in [0, m])$；
  令 $dp[i][j]$ 表示状态 $(i, j)$ 下该背包得到的最大价值，即前 $i$ 种物品（每种物品可以选择无限件）恰好放入容量为 $j$ 的背包所得到的最大总价值；

  第二步：列出状态转移方程；

$$dp[i][j] = max(dp[i-1][j - c[i] * k] + w[i] * k)$$

$$(0 \le k \le \frac {j} {c[i]})$$

• 因为每种物品有无限种可放置，将它归类为以下两种情况：
    1）不放：如果 “第 $i$ 种物品不放入容量为 $j$ 的背包”，那么问题转化成求 “前 $i-1$ 种物品放入容量为 $j$ 的背包” 的问题；由于不放，所以最大价值就等于 “前 $i-1$ 种物品放入容量为 $j$ 的背包” 的最大价值，对应状态转移方程中 $k = 0$ 的情况， 即 $dp[i-1][j]$；
    2）放 k 个：如果 “第 $i$ 种物品放入容量为 $j$ 的背包”，那么问题转化成求 “前 $i-1$ 种物品放入容量为 $j-c[i]*k$ 的背包” 的问题；那么此时最大价值就等于 “前 $i-1$ 种物品放入容量为 $j-c[i]*k$ 的背包” 的最大价值 加上放入 $k$ 个第 $i$ 种物品的价值，即 $dp[i-1][j - c[i]*k] + w[i]*k$；
    枚举所有满足条件的 $k$ 就是我们所求的 “前 $i$ 种物品恰好放入容量为 $j$ 的背包” 的最大价值了。注意：由于每件物品都可以无限选择，所以这里描述的时候都是用的 “种” 作为单位，即代表不同种类的物品。

  对于 $n$ 种物品放入一个容量为 $m$ 的背包，状态数为 $O(nm)$，每次状态转移的消耗为 $O(k)$，所以整个状态转移的过程时间复杂度是大于 $O(nm)$ 的，那么实际是多少呢？考虑最坏情况下，即 $c[i] = 1$ 时，那么要计算的 $dp[i][j]$ 的转移数为 $j$，总的状态转移次数就是 $\frac {m(m + 1)} {2}$，所以整个算法的时间复杂度是 $O(nm^2)$ 的，也就是说状态转移均摊时间复杂度是 $O(m)$ 的。

  我们把状态转移方程进行展开后得到如下的 $k+1$ 个式子：

$$dp[i][j] = max \begin{cases} dp[i-1][j] & (1)\\ dp[i-1][j - c[i]] + w[i] & (2)\\ dp[i-1][j - c[i]*2] + w[i]*2 & (3)\\ ... \\ dp[i-1][j - c[i]*k] + w[i] *k & (k+1) \end{cases}$$

  利用待定系数法，用 $j-c[i]$ 代替上式的 $j$ 得到如下式子：

$$dp[i][j-c[i]] = max \begin{cases} dp[i-1][j-c[i]] & (1)\\ dp[i-1][j - c[i]*2] + w[i] & (2)\\ dp[i-1][j - c[i]*3] + w[i]*2 & (3)\\ ... \\ dp[i-1][j - c[i]*k] + w[i] *(k-1) & (k) \end{cases}$$

  等式两边都加上 $w[i]$ 得到：

$$dp[i][j-c[i]] + w[i] = max \begin{cases} dp[i-1][j-c[i]] + w[i] & (1)\\ dp[i-1][j - c[i]*2] + w[i]*2 & (2)\\ dp[i-1][j - c[i]*3] + w[i]*3 & (3)\\ ... \\ dp[i-1][j - c[i]*k] + w[i] *k & (k) \end{cases}$$

  于是我们发现，这里的 $(1)...(k)$ 式子等价于最开始的状态转移方程中的 $(2) ... (k+1)$ 式，所以原状态转移方程可以简化为：$$dp[i][j] = max(dp[i-1][j], dp[i][j-c[i]] + w[i])$$
  这样就把原本均摊时间复杂度为 $O(m)$ 的状态转移优化到了 $O(1)$。
  那么我们来理解一下这个状态转移方程的含义：对于第 $i$ 种物品，其实只有两种选择：一个都不放、至少放一个；一个都不放 就是 “前 $i-1$ 种物品放满一个容量为 $j$ 的背包” 的情况，即 $dp[i-1][j]$；至少放一个 的话，我们尝试在 “前 $i$ 种物品放满一个容量为 $j$ 的背包” 里拿掉 1 个物品，即 “前 $i$ 种物品放满一个容量为 $j-c[i]$ 的背包”，这时候的值就是 $dp[i][j-c[i]] + w[i]$。取两者的大者就是答案了。
  其实这个思路我可以在本文开头就讲，也容易理解，之所以引入优化以及逐步推导的过程，就是想告诉读者，很多动态规划的问题是不能套用模板的，从简单的思路出发，加上一些推导和优化，逐步把复杂的问题循序渐进的求出来，才是解决问题的普遍思路。
  有关完全背包的更多内容，可以参考：夜深人静写算法（十五）- 完全背包。

3、多重背包

  有 $n(n \le 100)$ 种物品和一个容量为 $m(m \le 10000)$ 的背包。第 $i$ 种物品的容量是 $c[i]$，价值是 $w[i]$。现在需要选择一些物品放入背包，每种物品可以选择 $x[i]$ 件，并且总容量不能超过背包容量，求能够达到的物品的最大总价值。

  以上就是多重背包问题的完整描述，和 0/1 背包、完全背包的区别就是每种物品的选取有物品自己的值域限制，即文中红色字体标注的内容；
  第一步：设计状态；
  状态 $(i, j)$ 表示前 $i$ 种物品恰好放入容量为 $j$ 的背包 $(i \in [0, n], j \in [0, m])$；
  令 $dp[i][j]$ 表示状态 $(i, j)$ 下该背包得到的最大价值，即前 $i$ 种物品（每种物品可以选择 $x[i]$ 件）恰好放入容量为 $j$ 的背包所得到的最大总价值；

  第二步：列出状态转移方程；

$$dp[i][j] = max(dp[i-1][j - c[i] * k] + w[i] * k) \\ (0 \le k \le x[i])$$

因为每种物品有 $x[i]$ 种可放置，将它归类为以下两种情况：
  1）不放：如果 “第 $i$ 种物品不放入容量为 $j$ 的背包”，那么问题转化成求 “前 $i-1$ 种物品放入容量为 $j$ 的背包” 的问题；由于不放，所以最大价值就等于 “前 $i-1$ 种物品放入容量为 $j$ 的背包” 的最大价值，对应状态转移方程中 $k = 0$ 的情况， 即 $dp[i-1][j]$；
  2）放 k 个：如果 “第 $i$ 种物品放入容量为 $j$ 的背包”，那么问题转化成求 “前 $i-1$ 种物品放入容量为 $j-c[i] * k$ 的背包” 的问题；那么此时最大价值就等于 “前 $i-1$ 种物品放入容量为 $j-c[i] * k$ 的背包” 的最大价值 加上放入 $k$ 个第 $i$ 种物品的价值，即 $dp[i-1][j - c[i]*k] + w[i] * k$；
  枚举所有满足条件的 $k$ 就是我们所求的 “前 $i$ 种物品恰好放入容量为 $j$ 的背包” 的最大价值了。
  多重背包问题是背包问题的一般情况，每种物品有自己的值域限制。如果从状态转移方程出发，我们可以把三种背包问题进行归纳统一，得到一个统一的状态转移方程如下：

$$dp[i][j] = max(dp[i-1][j - c[i]*k] + w[i] * k)$$

  对于 0/1 背包问题， $k$ 的取值为 $0,1$；
  对于完全背包问题， $k$ 的取值为 $0, 1, 2, 3, ..., \lfloor \frac j {c[i]} \rfloor$；
  对于多重背包问题， $k$ 的取值为 $0, 1, 2, 3, ..., x[i]$；
  对于 $n$ 种物品放入一个容量为 $m$ 的背包，状态数为 $O(nm)$，每次状态转移的消耗为 $O(x[i])$，所以整个状态转移的过程时间复杂度是大于 $O(nm)$ 的，那么实际是多少呢？
  考虑最坏情况下，即 $x[i] = m$ 时，那么要计算的 $dp[i][j]$ 的转移数为 $j$，总的状态转移次数就是 $\frac {m(m + 1)} {2}$，所以整个算法的时间复杂度是 $O(nm^2)$ 的，也就是说状态转移均摊时间复杂度是 $O(m)$ 的。
  一个容易想到的优化是：我们可以将每种物品拆成 $x[i]$ 个，这样变成了 $\sum_{i=1}^n x[i]$ 个物品的 0/1 背包问题，我们知道 0/1 背包问题优化完以后，空间复杂度只和容量有关，即 $O(m)$。
  所以多重背包问题的空间复杂度至少是可以优化到 $O(m)$ 的。
  然而， 如果这样拆分，时间复杂度还是没有变化，但是给我们提供了一个思路，就是每种物品是可以拆分的。假设有 $x[i]$ 个物品，我们可以按照 2 的幂进行拆分，把它拆分成：

$$1, 2, 4, ..., 2^{k-1}, x[i] - 2^{k} + 1$$

  其中 $k$ 是最大的满足 $x[i] - 2^{k} + 1 \ge 0$ 的非负整数。
  这样，1 到 $x[i]$ 之间的所有整数都能通过以上 $k+1$ 个数字组合出来，所以只要拆成以上 $k+1$ 个物品，所有取 $k (0 \le k \le x[i])$ 个物品的情况都能被考虑进来。
  举例说明，当 $x[i] = 14$ 时，可以拆分成 1,2,4,7 个物品，那么当我们要取 13 个这类物品的时候，相当于选择 2、4、7，容量分别为 $c[i]*2, c[i]*4, c[i]* 7$, 价值分别为 $w[i]*2, w[i]*4, w[i]* 7$。
  通过这种拆分方式， $x[i]$ 最多被拆分成 $log_2 {x[i]}$ 个物品，然后再用 0/1 背包求解，得到了一个时间复杂度为 $O(m\sum_{i=1}^{n}log_2{x[i]})$ 的算法。
  有关多重背包的更多内容，可以参考：夜深人静写算法（十六）- 多重背包。

4、分组背包

  有 $n(n \le 1000)$ 个物品和一个容量为 $m(m \le 1000)$ 的背包。这些物品被分成若干组，第 $i$ 个物品属于 $g[i]$ 组，容量是 $c[i]$，价值是 $w[i]$，现在需要选择一些物品放入背包，并且每组最多放一个物品，总容量不能超过背包容量，求能够达到的物品的最大总价值。

  以上就是分组背包问题的完整描述，和其它背包问题的区别就是每个物品多了一个组号，并且相同组内，最多只能选择一个物品放入背包；因为只有一个物品，所以读者可以暂时忘掉 完全背包 和 多重背包 的概念，在往下看之前，先回忆一下 0/1 背包的状态转移方程。

  第一步：预处理；
  首先把每个物品按照组号 $g[i]$ 从小到大排序，假设总共有 $t$ 组，则将 $g[i]$ 按顺序离散到 $[1,t]$ 的正整数。这样做的目的是为了将 $g[i]$ 作为下标映射到状态数组中；

  第二步：设计状态；
  状态 $(k, j)$ 表示前 $k$ 组物品恰好放入容量为 $j$ 的背包 $(k \in [0, t], j \in [0, m])$；令 $dp[k][j]$ 表示状态 $(k, j)$ 下该背包得到的最大价值，即前 $k$ 组物品（每组物品至多选一件）恰好放入容量为 $j$ 的背包所得到的最大总价值；

  第三步：列出状态转移方程：

$$dp[k][j] = max(dp[k-1][j], dp[k-1][j - c[i]] + w[i])$$

$$k = g[i]$$

因为每个物品有只有两种情况：
  1）不放：如果 “第 $i$ 个物品（属于第 $k$ 组）不放入容量为 $j$ 的背包”，那么问题转化成求 “前 $k-1$ 组物品放入容量为 $j$ 的背包” 的问题；由于不放，所以最大价值就等于 “前 $k-1$ 组物品放入容量为 $j$ 的背包” 的最大价值，对应状态转移方程中的 $dp[k-1][j]$；
  2）放：如果 “第 $i$ 个物品（属于第 $k$ 组）放入容量为 $j$ 的背包”，那么问题转化成求 “前 $k-1$ 组物品放入容量为 $j-c[i]$ 的背包” 的问题；那么此时最大价值就等于 “前 $k-1$ 组物品放入容量为 $j-c[i]$ 的背包” 的最大价值 加上放入第 $i$ 个物品的价值，即 $dp[k-1][j - c[i]] + w[i]$；
  因为 前 $k-1$ 组物品中一定不存在第 $k$ 组中的物品，所以能够满足 “最多放一个” 这个条件；

  对于 $n$ 个物品放入一个容量为 $m$ 的背包，状态数为 $O(nm)$，每次状态转移的消耗为 $O(1)$，所以整个状态转移的过程时间复杂度是 $O(nm)$；
  注意在分组背包求解的时候，要保证相同组的在一起求，而一开始的预处理和离散化正式为了保证这一点，这样，每个物品的组号为 $g[i] = 1,2,3,4...,t$，并且我们可以把状态转移方程进一步表示成和 $k$ 无关的，如下：

$$dp[ g[i] ][j] = max(dp[ g[i]-1][j], dp[ g[i]-1][j - c[i]] + w[i])$$

  有关分组背包更加详细的内容，可以参考：夜深人静写算法（十七）- 分组背包。

5、依赖背包

  商店里有 $n(n \le 50)$ 个盒子，每个盒子价钱为 $p[i](p[i] \le 1000)$，价值为 0，盒子里面有一些小礼物，数量为 $m[i](1 \le m[i] \le 10)$，每个小礼物描述成一个二元组 $(c, v)$， $c$ 为价钱， $v$ 为价值，如果要买小礼物，必须先买盒子。现在给出价钱 $m(m \le 100000)$，求能够买到的最大价值。

  这是一个比较特殊的依赖性背包问题，也是依赖背包中最简单的情况，其中盒子作为 主件，小礼物作为 附件。想要购买附件，必须先购买主件，此所谓 “依赖” ；

  第一步：设计状态；
  状态 $(i, j)$ 表示前 $i$ 个盒子购买的价钱恰好为 $j$ $(i \in [0, n], j \in [0, m])$；
  令 $dp[i][j]$ 表示状态 $(i, j)$ 下得到的最大价值，即前 $i$ 个盒子购买价钱为 $j$ 的情况下所得到的最大总价值；

  我们在设计状态的时候，没有把小礼物设计到状态里，那么如何进行状态转移呢？

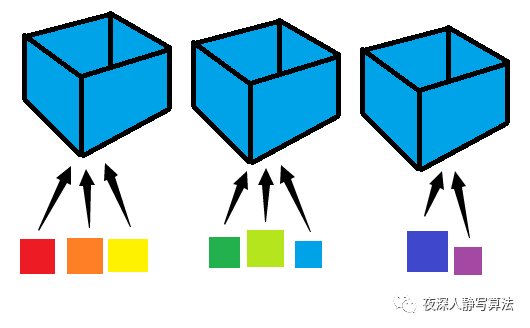
  可以这么考虑，抛开小礼物不说，每个盒子其实只有两种状态，选 和 不选；
  1）选：就是要对这个盒子里的小礼物进行一次 0/1 背包；
  2）不选：就和这盒子里的小礼物无关了，直接等于前 $i-1$ 个盒子的最大价值，即 $dp[i-1][j]$。
  那么，只要从前往后枚举所有盒子， $p[i]$ 为第 $i$ 个盒子的价钱， $w[i]$ 为价值，由于这个问题下盒子是没有价值的，即 $w[i]$ 恒等于零；

进行如下三步操作：
  1）首先，买第 $i$ 个盒子，并且不放物品；
  2）然后，既然盒子都已经买下来了，就可以放心对第 $i$ 个盒子里的小礼物进行 0/1 背包了；
  3）最后，对 买盒子 $i$ 和 不买盒子 $i$ 取一次最大价值；

  买第 $i$ 个盒子，不放物品的情况肯定是从前 $i-1$ 个盒子的状态推算过来的，给出状态转移方程如下：

$$dp[i][j] =\begin{cases}inf & j < p[i] & (1)\\dp[i-1][j - p[i]]+w[i] & j \ge p[i] & (2)\end{cases}$$

• (1) 代表钱不够，无限凄凉；(2) 代表从 前 $i-1$ 个盒子价格为 $j - p[i]$ 时，再花 $p[i]$ 买下第 $i$ 个盒子的情况。这时候 $dp[i][j]$ 代表的是 第 $i$ 个盒子买下后，还没买小礼物时，容量为 $j$ 的最大总价值；

  既然盒子都已经买下来了，就可以放心对第 $i$ 个盒子里的小礼物在 $dp[i][0...m]$ 上进行 0/1 背包了；所有小礼物都枚举完毕以后，得到的 $dp[i][j]$ 代表的是 第 $i$ 个盒子买下，并且买了若干小礼物后，容量为 $j$ 的最大总价值；

  最后，对买 这个盒子 和 不买这个盒子 做一次选择，即取一次最大价值，如下：

$$dp[i][j] = max(dp[i][j], dp[i-1][j])$$

  这里的 $dp[i-1][j]$ 正代表的是第 $i$ 个盒子不买的情况。
  有关依赖背包的更多内容，可以参考：夜深人静写算法（十八）- 依赖背包。

六、树形DP

  给定一棵 $n(n <= 150)$ 个结点的树，去掉一些边，使得正好出现一个 $P$ 个结点的连通块。问去掉最少多少条边能够达到这个要求。

  如图所示，一棵 10 个结点的树，我们可以去掉图中红色的边，变成两棵子树，分别为 3 个结点和 7个结点。

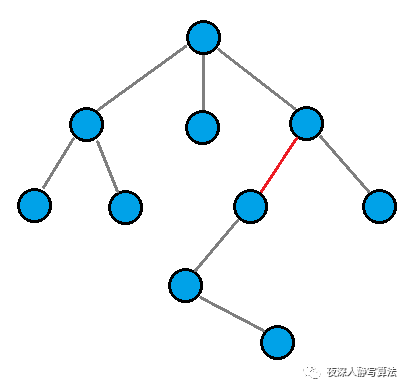
  也可以通过这样的方式，得到三颗子树，分别为 5 、4、1 个结点。

  对于树上的某个结点（如图的红色结点），可以选择去掉连接子树的边，也可以选择留着；每条连接子树的边的 选 和 不选，能够得到一个组合，对应了背包问题，而每棵子树的选择只能选择一种，对应了分组背包，所以可以利用这个思路来设计状态。

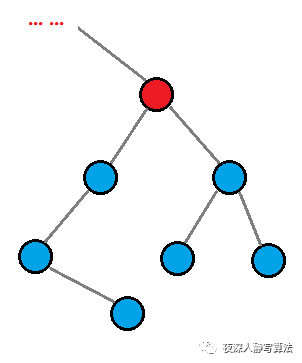
  状态设计：用 $dp[u][x]$ 表示以 $u$ 为根的子树，能够通过去掉一些边而得到一个正好是 $x$ 结点的连通块（注意只包含它的子树的部分，不连接它的父结点）的最少消耗；
  状态转移思路：枚举 $u$ 的所有子结点，对于子结点 $v$，递归计算 $dp[v][i] (1 <= i <= x)$ 所有的可能情况，如果 $dp[v][i]$ 存在，则认为这是一个容量为 $i$，价值为 $dp[v][i]$ 的物品，表示为 $(i, dp[v][i])$。然后在结点 $u$ 的背包上进行一次分组背包。
  初始情况：对于任何一个结点 $u$，它的子结点个数为 $c_u$，初始情况是 $dp[u][1] = c_u$，表示如果以当前这个结点为孤立点，那么它的子树都不能选，所以费用就是去掉所有连接子树的边，即子树的个数。
  状态转移：然后对于每棵子树 $v$ 的 $k$ 个结点的连通块，答案就是 $dp[v][j-k] + dp[v][k] - 1$，注意这里的 -1 的含义，因为我们一开始默认将所有连接子树的边去掉，所以这里需要补回来。
  答案处理：最后的答案就是 $\min(dp[x][P] + (1 \ if \ x \ is \ not \ root)$；考虑结点为 P 的连通块只会出现在两个地方：1）和根结点相连的块，那么答案就是 $dp[root][P]$；2）不和根结点相连的块，需要枚举所有结点的 $dp[x][P] +1$ 取最小值，其中这里的 1 代表斩断 $(parent[x], x)$ 这条边的消耗；

---

👉🏻下一篇：❤️四万字《画解动态规划》从入门到精通（下）❤️