前言

  「 动态规划 」作为算法中一块比较野的内容，没有比较系统的分类，只能通过不断总结归纳，对各种类型进行归类。「 动态规划 」（即 Dynamic programming，简称 DP）是一种在数学、管理科学、计算机科学 以及 生物信息学中使用的，通过把原问题分解为相对简单的「 子问题 」的方式求解「 复杂问题 」的方法。
  「 动态规划 」是一种算法思想：若要解一个给定问题，我们需要解其不同部分（即「 子问题 」），再根据「 子问题 」的解以得出原问题的解。要理解动态规划，就要理解 「 最优子结构 」 和 「 重复子问题 」。
  本文将针对以下一些常用的动态规划问题，进行由浅入深的系统性讲解。首先来看一个简单的分类，也是今天本文要讲的内容。

直接跳到末尾 参与投票，获取粉丝专属福利。

一、递推问题

  递推问题作为动态规划的基础，是最好掌握的，也是必须掌握的，它有点类似于高中数学中的数列，通过 前几项的值 推导出 当前项的值。

1、一维递推

  你正在爬楼梯，需要 $n$ 阶你才能到达楼顶。每次你可以爬 $1$ 或 $2$ 个台阶。你有多少种不同的方法可以爬到楼顶呢？

  假设我们已经到了第 $n$ 阶楼梯，那么它可以是从 $n-1$ 阶过来的，也可以是从 $n-2$ 阶过来的（但是，不可能是从 $n-3$ 阶直接过来的），所以如果达到第 $n$ 阶的方案数为 $f[n]$，那么到达 $n-1$ 阶就是 $f[n-1]$，到达 $n-2$ 阶 就是 $f[n-2]$，所以可以得出：

$$f[n] = f[n-1] + f[n-2]$$

  其中，当 $n=0$ 时方案数为 1，代表初始情况； $n=1$ 时方案数为 1，代表走了一步，递推计算即可。
  以上就是最简单的动态规划问题，也是一个经典的数列：斐波那契数列 的求解方式。它通过一个递推公式，将原本指数级的问题转化成了线性的，时间复杂度为 $O(n)$。
  C语言代码实现如下：

int f[1000];
int climbStairs(int n){
    f[0] = f[1] = 1;
    for(int i = 2; i <= n; ++i) {
        f[i] = f[i-1] + f[i-2];
    }
    return f[n];
}

2、二维递推

  给定一个非负整数 $n$，生成杨辉三角的前 $n$ 行。在杨辉三角中，每个数是它 左上方 和 右上方 的数的和。

  根据杨辉三角的定义，我们可以简单将上面的图进行一个变形，得到：

于是，我们可以得出以下结论：
  1）杨辉三角的所有数可以存储在一个二维数组中，行代表第一维，列代表第二维度；
  2）第 $i$ 行的元素个数为 $i$ 个；
  3）第 $i$ 行 第 $j$ 列的元素满足公式：

$$c[i][j] = \begin{cases} 1 & i=0\\ c[i-1][j-1] + c[i-1][j] & otherwise \end{cases}$$

  于是就可以两层循环枚举了。时间复杂度为 $O(n^2)$。
  C语言代码实现如下：

int c[40];
void generate(int n) {
    for(int i = 0; i < n; ++i) {
        for(int j = 0; j <= i; ++j) {
            if(j == 0 || j == i) {
                c[i][j] = 1;
            }else {
                c[i][j] = c[i-1][j-1] + c[i-1][j];
            }
        }
    }
}

二、线性DP

1、最小花费

  数组的每个下标作为一个阶梯，第 $i$ 个阶梯对应着一个非负数的体力花费值 $cost[i]$（下标从 0 开始）。每当爬上一个阶梯，都要花费对应的体力值，一旦支付了相应的体力值，就可以选择 向上爬一个阶梯 或者 爬两个阶梯。求找出达到楼层顶部的最低花费。在开始时，可以选择从下标为 $0$ 或 $1$ 的元素作为初始阶梯。

  令走到第 $i$ 层的最小消耗为 $f[i]$。假设当前的位置在 $i$ 层楼梯，那么只可能从 $i-1$ 层过来，或者 $i-2$ 层过来；
    如果从 $i-1$ 层过来，则需要消耗体力值： $f[i-1] + cost[i-1]$；
    如果从 $i-2$ 层过来，则需要消耗体力值： $f[i-2] + cost[i-2]$；
  起点可以在第 0 或者 第 1 层，于是有状态转移方程：

$$f[i] = \begin{cases} 0 & i=0,1\\ \min ( f[i-1] + cost[i-1], f[i-2] + cost[i-2] ) & i > 1\end{cases}$$

  这个问题和一开始的递推问题的区别在于：一个是求前两项的和，一个是求最小值。这里就涉及到了动态取舍的问题，也就是动态规划的思想。
  如果从前往后思考，每次都有两种选择，时间复杂度为 $O(2^n)$。转化成动态规划以后，只需要一个循环，时间复杂度为 $O(n)$。
  C语言代码实现如下：

int f[1024];
int min(int a, int b) {
    return a < b ? a : b;
}
int minCostClimbingStairs(int* cost, int costSize){
    f[0] = 0;
    f[1] = 0;
    for(int i = 2; i <= costSize; ++i) {
        f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2]);
    }
    return f[costSize];
}

2、最大子段和

  给定一个整数数组 $nums$ ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

  由于要求的是连续的子数组，所以对于第 $i$ 个元素，状态转移一定是从 $i-1$ 个元素转移过来的。基于这一点，可以令 $f[i]$ 表示以 $i$ 号元素结尾的最大值。
  那么很自然，这个最大值必然包含 $nums[i]$ 这个元素，那么要不要包含 $nums[i-1],nums[i-2],nums[i-3],...,nums[k]$ 呢？其实就是看第 $i-1$ 号元素结尾的最大值是否大于零，也就是：当 $f[i-1] \le 0$ 时，则 前 $i-1$ 个元素是没必要包含进来的。所以就有状态转移方程：

$$f[i] = \begin{cases} nums[0] & i = 0 \\ nums[i] & f[i-1] \le 0 \\ nums[i] + f[i-1] & f[i-1] > 0\end{cases}$$

一层循环枚举后，取 $max(f[i])$ 就是答案了。只需要一个循环，时间复杂度为 $O(n)$。
  C语言代码实现如下：

int dp[30010];
int max(int a, int b) {
    return a > b ? a : b;
}

int maxSubArray(int* nums, int numsSize){
    int maxValue = nums[0];
    dp[0] = nums[0];
    for(int i = 1; i < numsSize; ++i) {
        dp[i] = nums[i];
        if(dp[i-1] > 0) {
            dp[i] += dp[i-1];
        }
        maxValue = max(maxValue, dp[i]);
    }
    return maxValue;
}

3、最长单调子序列

  给定一个长度为 $n(1 \le n \le 1000)$ 的数组 $a_i$，求给出它的最长递增子序列的长度。

  在看这个问题之前，我们先来明确一些概念：单调序列、单调子序列、最大长单调子序列。
  单调序列 就是一个满足某种单调性的数组序列，比如 单调递增序列、单调递减序列、单调不增序列、单调不减序列。举几个简单的例子：
  单调递增序列：1，2，3，7，9
  单调递减序列：9，8，4，2，1
  单调不增序列：9，8，8，5，2
  单调不减序列：1，2，2，5，5
  一个比较直观的单调递增序列的例子就是一个楼梯的侧面。

  我们可以把这个楼梯每一阶的高度用一个数字表示，得到一个单调递增序列，如图所示：

  单调子序列 指的是任意一个数组序列，按顺序选择一些元素组成一个新的序列，并且满足单调性。对于一个长度为 $n$ 的序列，每个元素可以选择 “取” 或者 “不取”，所以最多情况下，有 $2^n$ 个单调子序列。
  如图所示，代表的是序列：[1，2，4，6，3，5，9]

  其中 [1，2，6] 为它的一个长度为 3 的单调子序列，如图所示；

  [1，3，6] 则不是，因为 3 和 6 的顺序不是原序列中的顺序；[1，4，3] 也不是，因为它不满足单调性。
  最长单调子序列 是指对于原数组序列，能够找到的元素个数最多的单调子序列。
  还是以 [1，2，4，6，3，5，9] 为例，它的最长单调子序列为：[1，2，4，6，9]，长度为 5；

  当然，也可以是 [1，2，3，5，9]，长度同样为 5。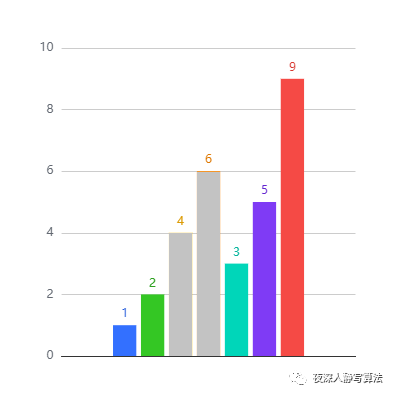   那么，接下来，我们看下如何通过动态规划的方法来求解 最长递增子序列。
  对于数组序列 $a_i(1 \le i \le n)$，令 $f[i]$ 表示以第 $i$ 个数 $a_i$ 结尾的最长递增子序列的长度。那么，我们考虑以第 $i$ 个数 $a_i$ 结尾的最长递增子序列，它在这个序列中的前一个数一定是 $a_j(1 \le j < i)$ 中的一个，所以，如果我们已经知道了 $f[j]$，那么就有 $f[i] = f[j] + 1$。显然，我们还需要满足 $a_j < a_i$ 这个递增的限制条件。
  那么就可以得出状态转移方程：

$$f[i] = \max_{j=1}^{i-1} (f[j] \ | \ a_j < a_i) + 1$$

  这里 $f[j]$ 是 $f[i]$ 的子结构，而 $max(f[j])$ 是 $f[i]$ 的最优子结构，当然我们需要考虑一种情况，就是没有找到最优子结构的时候，例如： $i=1$ 或者 不存在 $a_j < a_i$ 的 $j$，此时 $f[i] = 1$，表示 $a_i$ 本身是一个长度为 $1$ 的最长递增子序列。
   $f[i]$ 数组可以通过两层循环来求解，如下图表所示：

-|-|-|-|-|-|-|-
$a[i]$|1|2|4|6|3|5|9
$f[i]$|1|2|3|4|3|4|5

  状态数 $f[...]$ 总共 $O(n)$ 个，状态转移的消耗为 $O(n)$，所以总的时间复杂度为 $O(n^2)$，所以对于这类问题，一般能够接受的 $n$ 的范围在千级别，也就是 $1000, 2000, 3000 ...$。如果是 $n=10000, 100000$ 的情况，就需要考虑优化了。
  有关最长单调子序列的问题，还有 $O(nlog_2n)$ 的优化算法，具体方法可以参考以下文章：夜深人静写算法（二十）- 最长单调子序列。

三、二维DP

1、最长公共子序列

  给定两个数组序列 $a_1, a_2, ..., a_n$ 和 $b_1, b_2, ..., b_m$，其中 $n,m \le 1000$，求两个数组的最长公共子序列。

  考虑两个数组序列 $a_1, a_2, ..., a_n$ 和 $b_1, b_2, ..., b_m$，对于 $a$ 序列中第 $i$ 个元素 $a_i$ 和 $b$ 序列中的第 $j$ 个元素 $b_j$，有两种情况：
   $(1)$ 相等即 $a_i == b_j$ 的情况，这个时候如果前缀序列 $a_1, a_2, ..., a_{i-1}$ 和 $b_1, b_2, ..., b_{j-1}$ 的最长公共子序列已经求出来了，记为 $x$ 的话，那么很显然，在两个序列分别加入 $a_i$ 和 $b_j$ 以后，长度又贡献了 1，所以 $a_1, a_2, ..., a_{i}$ 和 $b_1, b_2, ..., b_{j}$ 的最长公共子序列就是 $x+1$；

   $(2)$ 不相等即 $a_i \neq b_j$ 的情况，这个时候我们可以把问题拆分成两个更小的子问题，即 分别去掉 $a_i$ 和 $b_j$ 的情况，如图所示：

  去掉 $a_i$ 以后，问题转变为求： $a_1, a_2, ..., a_{i-1}$ 和 $b_1, b_2, ..., b_{j}$ 的最长公共子序列；
  去掉 $b_j$ 以后，问题转变为求： $a_1, a_2, ..., a_{i}$ 和 $b_1, b_2, ..., b_{j-1}$ 的最长公共子序列；
  根据上面的两种情况的讨论，我们发现，在任何时候，我们都在求 $a$ 的前缀 和 $b$ 的前缀的最长公共序列，所以可以这么定义状态：用 $f[i][j]$ 表示 $a_1, a_2, ..., a_{i}$ 和 $b_1, b_2, ..., b_{j}$ 的最长公共子序列。
  在设计状态的过程中，我们已经无形中把状态转移也设计好了，状态转移方程如下：

$$f[i][j] = \begin{cases}0 & i=0\ or\ j=0 \\ f[i-1][j-1] + 1 & i,j>0,a_i=b_j \\ \max(f[i][j-1], f[i-1][j]) & i,j>0,a_i \neq b_j\end{cases}$$

  对于 $i=0$ 或者 $j=0$ 代表的是：其中一个序列的长度为 0，那么最长公共子序列的长度肯定就是 0 了；
  其余两种情况，就是我们上文提到的 $a_i$ 和 $b_j$ “相等” 与 “不相等” 的两种情况下的状态转移。如图所示，代表了字符串 “GATCGTGAGC” 和 “AGTACG” 求解最长公共子序列的 $f[i][j] (i,j > 0)$ 的矩阵。

  对于长度分别为 $n$ 和 $m$ 的两个序列，求解它们的最长公共子序列时，状态数总共有 $O(nm)$ 个，每次状态转移的消耗为 $O(1)$，所以总的时间复杂度为 $O(nm)$。
  对于 $f[i][j]$ 这个状态，求解过程中，只依赖于 $f[i][j-1]$、 $f[i-1][j-1]$、 $f[i-1][j]$。

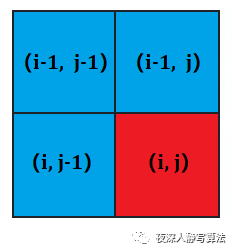
  即每次求解只需要有 上一行 和 这一行 的状态即可，所以可以采用滚动数组进行优化，将状态转移方程变成：

$$f[cur][j] = \begin{cases}f[last][j-1] + 1 & j>0,a_i=b_j \\ \max(f[cur][j-1], f[last][j]) & j>0,a_i \neq b_j\end{cases}$$

  只需要简单将 $i$ 替换成 $cur$， $i-1$ 替换成 $last$ 即可。这样就把原本 $O(nm)$ 的空间复杂度变成了 $O(p)$，其中 $p = \min(n,m)$。

• 优化后的 C++ 代码实现如下：

typedef char ValueType;
const int maxn = 5010;
int f[2][maxn];

int getLCSLength(int hsize, ValueType *h, int vsize, ValueType *v) {
    memset(f, 0, sizeof(f));
    int cur = 1, last = 0;
    for (int i = 1; i <= vsize; ++i) {
        for (int j = 1; j <= hsize; ++j) {
            if (v[i] == h[j])
                f[cur][j] = f[last][j - 1] + 1;
            else
                f[cur][j] = max(f[cur][j - 1], f[last][j]);
        }
        swap(last, cur);
    }
    return f[last][hsize];
}

  有关于 最长公共子序列 的更多内容，可以参考以下内容：夜深人静写算法（二十一）- 最长公共子序列。

2、最小编辑距离

  长度为 $n$ 的源字符串 $a_1,a_2,...,a_n$，经过一些给定操作变成长度为 $m$ 的目标字符串 $b_1,b_2,...b_m$，操作包括如下三种：
  1） $Insert$：在源字符串中插入一个字符，插入消耗为 $I$；
  2） $Delete$：在源字符串中删除一个字符，删除消耗为 $D$；
  3） $Replace$：将源字符串中的一个字符替换成另一个字符，替换消耗为 $R$；
求最少的总消耗，其中 $n,m \le 1000$。

  令 $f[i][j]$ 表示源字符串 $a_1,a_2,...,a_i$ 经过上述三种操作变成目标字符串 $b_1,b_2,...b_j$ 的最少消耗。
  假设 $a_1,a_2,...,a_{i}$ 变成 $b_1,b_2,...b_{j-1}$ 的最少消耗已经求出，等于 $f[i][j-1]$，则需要在 $a[i]$ 的后面插入一个字符 $b_j$，那么产生的消耗为：$$f[i][j-1] + I$$ 如图所示，源字符串为 “AGTA”，目标字符串为 “GATCGT” 的情况下，将源字符串变成 "“GATCG” 的最小消耗为 $f[i][j-1]$，那么只要在源字符串最后再插入一个 ‘T’，就可以把源字符串变成目标字符串 “GATCGT”；

  假设 $a_1,a_2,...,a_{i-1}$ 变成 $b_1,b_2,...b_{j}$ 的最少消耗已经求出，等于 $f[i-1][j]$，则需要把 $a_i$ 个删掉，那么产生的消耗为：$$f[i-1][j] + D$$ 如图所示，源字符串为 “AGTA”，目标字符串为 “GATCGT” 的情况下，将 “AGT” 变成目标字符串的最小消耗为 $f[i-1][j]$，那么只要把源字符串最后一个’A’删掉，就可以把源字符串变成目标字符串；

  假设 $a_1,a_2,...,a_{i-1}$ 变成 $b_1,b_2,...b_{j-1}$ 的最少消耗已经求出，等于 $f[i-1][j-1]$，则将 $a_i$ 替换成 $b_j$， $a_1,a_2,...,a_{i}$ 就可以变成 $b_1,b_2,...b_{j}$。替换时需要考虑 $a_i=b_j$ 和 $a_i \neq b_j$ 的情况，所以替换产生的消耗为：$$f[i-1][j-1] + \begin{cases} 0 & a_i=b_j \ R & a_i \neq b_j\end{cases}$$ 如图所示，源字符串为 “AGTA”，目标字符串为 “GATCGT” 的情况下，将 “AGT” 变成 “GATCGT” 的最小消耗为 $f[i-1][j-1]$，那么只要将 源字符串 的最后一个字符 替换为 目标字符串 的最后一个字符 ，就可以把源字符串变成目标字符串；替换时根据 源字符串 和 目标字符串 原本是否相等来决定消耗；

• 边界情况主要考虑以下几种：
    a. 空串变成目标串 即 $f[0][j]$，总共需要插入 $j$ 个字符，所以 $f[0][j] = f[0][j-1] + I$；
    b. 源字符串变成空串 即 $f[i][0]$，总共需要删除 $i$ 个字符，所以 $f[i][0] = f[i-1][0] + D$；
    c. 空串变成空串 即 $f[0][0] = 0$

  将上述所有状态进行一个整合，得到状态转移方程如下：

$$f[i][j] = \begin{cases}0 & i=0,j=0\\f[i][j-1]+I & i=0,j>0\\ f[i-1][j] + D & i>0,j=0 \\ \min_{i>0,j>0} \begin{cases} f[i][j-1] + I\\ f[i-1][j] + D\\ f[i-1][j-1] + R_{a_i \neq b_j}\end{cases}\end{cases}$$

  通过这个状态矩阵，最后计算得到 $f[n][m]$ 就是该题所求 "源字符串 $a_1,a_2,...,a_n$，经过 插入、删除、替换 变成目标字符串 $b_1,b_2,...b_m$" 的最少消耗了，特殊的，当 $I = D = R = 1$ 时， $f[n][m]$ 就是字符串 $a$ 和 $b$ 的莱文斯坦距离。
  状态总数 $O(nm)$，每次状态转移的消耗为 $O(1)$，所以总的时间复杂度为 $O(nm)$，空间上可以采用滚动数组进行优化，具体优化方案可以参考 最长公共子序列 的求解过程。
  如图所示的是一张源字符串 “AGTACG” 到目标字符串 “GATCGTGAGC” 的莱文斯坦距离图。

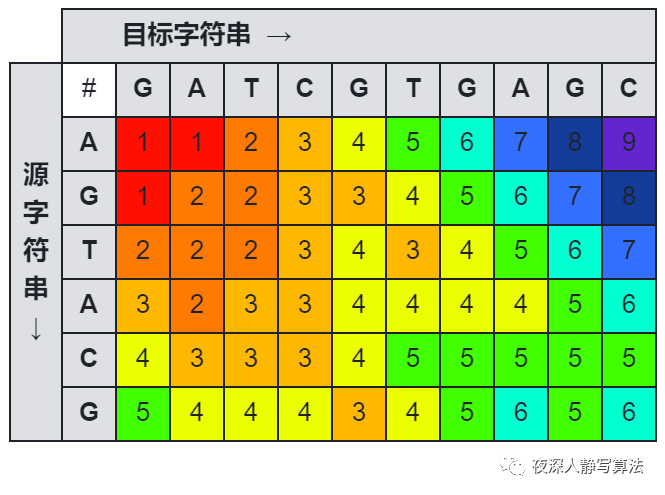
  有关最小编辑距离的详细内容，可以参考：夜深人静写算法（二十二）- 最小编辑距离。

3、双串匹配问题

  给定一个 匹配字符串 s (只包含小写字母) 和一个 模式字符串 p (包含小写字母和两种额外字符：'.'和 '*')，要求实现一个支持 '.'和 '*'的正则表达式匹配（'*'前面保证有字符）。
  '.'匹配任意单个字符
  '*'匹配零个或多个前面的那一个元素

  这是个经典的 串匹配 问题，可以按照 最长公共子序列 的思路去解决。令 $f(i, j)$ 代表的是 匹配串前缀 s[0:i] 和 模式串前缀 p[0:j] 是否有匹配，只有两个值： 0 代表 不匹配， 1 代表 匹配。
  于是，对模式串进行分情况讨论：
  1）当 p[j] 为.时，代表 s[i] 为任意字符时，它都能够匹配（没毛病吧？没毛病），所以问题就转化成了求 匹配串前缀 s[0:i-1] 和 模式串前缀 p[0:j-1] 是否有匹配的问题，也就是这种情况下 $f(i, j) = f(i-1, j-1)$，如图1所示：


  2）当 p[j] 为*时，由于*前面保证有字符，所以拿到字符 p[j-1]，分情况讨论：
    2.a）如果 p[j-1] 为.时，可以匹配所有 s[0:i] 的后缀，这种情况下，只要 $f(k, j-2)$ 为 1， $f(i, j)$ 就为 1；其中 $k \in [0, i]$。如下图所示：


    2.b）如果 p[j-1] 非.时，只有当 s[0:i] 的后缀 字符全为 p[j-1] 时，才能去匹配 s[0:i] 的前缀，同样转化成 $f(k, j-2)$ 的子问题。如下图所示：


  3）当 p[j] 为其他任意字符时，一旦 p[j] 和 s[i] 不匹配，就认为 $f(i, j) = 0$，否则 $f(i, j) = f(i-1, j-1)$，如下图所示：


  最后，这个问题可以采用 记忆化搜索 求解，并且需要考虑一些边界条件，边界条件可以参考代码实现中的讲解。记忆化搜索会在下文仔细讲解。
  匹配串的长度为 $n$，模式串的长度为 $m$。状态数： $O(nm)$，状态转移： $O(n)$，时间复杂度： $O(n^2m)$。

👉🏻下一篇：❤️四万字《画解动态规划》从入门到精通（中）❤️