- 微信
- 微博
  
  分享文章到微博
- 复制链接
  
  复制链接到剪贴板

❤️四万字《画解动态规划》从入门到精通（下）❤️

英雄哪里出来发表于 2021/09/17 19:42:33 2021/09/17

【摘要】《画解动态规划》下

七、矩阵二分

$A^n=\begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1m}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2m}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{m1}}&{a_{m2}}&{\cdots}&{a_{mm}}\\ \end{bmatrix}^n$

对于求矩阵的 $n$ 次幂，如果采用简单的连乘来求解，这个时间复杂度是完全无法接受的，我们联想到之前提到的整数的二分快速幂（夜深人静写算法（三十）- 二分快速幂），对于矩阵也是同样适用的；

$A^{n} = \begin{cases} I & n = 0\\ (A^{\frac{n-1}{2}})^2 \times A& n 为奇数\\ (A^{\frac{n}{2}})^2 & n 为非零偶数 \end{cases}$

再加上模加、模乘的性质，矩阵同样满足模幂运算，即：

$A^{n} \mod M = \begin{cases} I \mod M & n = 0\\ (A^{\frac{n-1}{2}})^2 \times A \mod M & n 为奇数\\ (A^{\frac{n}{2}})^2 \mod M & n 为非零偶数 \end{cases}$

如此一来，对于 $m$ 阶方阵 $A$ ，时间复杂度就可以降到 $O(m^3log_n)$ ；
还是回到本文开头的那个问题，如何计算斐波那契数列第 $n$ 项模上 $M$ ？相信聪明的读者已经想到了，我们的主角是：矩阵！
我们首先来看递推公式：

$f(n) = f(n-1) + f(n-2)$

然后我们联想到：1 个 $2 \times 2$ 的矩阵和 1 个 $2 \times 1$ 的矩阵相乘，得到的还是一个 $2 \times 1$ 的矩阵；
首先，利用递推公式填充列向量和矩阵：

$\left[ \begin{matrix} f(n) \\ ? \end{matrix} \right] = \left[ \begin{matrix} 1 & 1 \\ ? & ?\end{matrix} \right] \left[ \begin{matrix} f(n-1) \\ f(n-2)\end{matrix} \right]$

接下来利用列向量的传递性把带有问号的列向量补全，得到：

$\left[ \begin{matrix} f(n) \\ f(n-1)\end{matrix} \right] = \left[ \begin{matrix} 1 & 1 \\ ? & ?\end{matrix} \right] \left[ \begin{matrix} f(n-1) \\ f(n-2)\end{matrix} \right]$

再把带有问号的系数矩阵补全，得到：

$\left[ \begin{matrix} f(n) \\ f(n-1)\end{matrix} \right] = \left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right] \left[ \begin{matrix} f(n-1) \\ f(n-2)\end{matrix} \right]$

然后进行逐步化简，得到：

$\begin{aligned} \left[ \begin{matrix} f(n) \\ f(n-1)\end{matrix} \right] &= \left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right] \left[ \begin{matrix} f(n-1) \\ f(n-2)\end{matrix} \right] \\ &= \left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right] \left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right] \left[ \begin{matrix} f(n-2) \\ f(n-3)\end{matrix} \right] \\ &=\underbrace{ \left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right] {\cdots}\left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right] }_{n-1} \left[ \begin{matrix} f(1) \\ f(0)\end{matrix} \right] \\ \end{aligned}$

最后，根据矩阵乘法结合律，把前面的矩阵合并，得到：

$\begin{aligned} \left[ \begin{matrix} f(n) \\ f(n-1)\end{matrix} \right] &=\left[ \begin{matrix} 1 & 1 \\ 1 & 0\end{matrix} \right]^{n-1}\left[ \begin{matrix} f(1) \\ f(0)\end{matrix} \right] \\ &=A^{n-1}\left[ \begin{matrix} 1 \\ 0 \end{matrix} \right] \end{aligned}$

于是，只要利用矩阵二分快速幂求得 $A^{n-1} \mod M$ ，再乘上初始列向量 $\left[ \begin{matrix} 1 \\ 0 \end{matrix} \right]$ ，得到的列向量的第一个元素就是问题的解了；
事实上，只要列出状态转移方程，当 $n$ 很大时，我们就可以利用矩阵二分快速幂进行递推式的求解了。
有关矩阵二分的更加深入的内容，可以参考：夜深人静写算法（二十）- 矩阵快速幂。

八、区间DP

有 $n(n \le 100)$ 堆石子摆放成一排，第 $i$ 堆的重量为 $w_i$ ，现要将石子有次序地合并成一堆。规定每次只能选相邻的二堆合并成新的一堆，合并的消耗为当前合并石子的总重量。试设计出一个算法，计算出将 $n$ 堆石子合并成一堆的最小消耗。

在思考用动态规划求解的时候，我们可以先想想如果穷举所有方案，会是什么情况。
对于这个问题来说，我们第一个决策可以选择一对相邻石子进行合并，总共有 $n-1$ 种情况；对于 5堆石子的情况，第 1 次合并总共有 4 种选择：

1）选择第 1 堆和第 2 堆的石子进行合并，如图所示：
2）选择第 2 堆和第 3 堆的石子进行合并，如图所示：
3）选择第 3 堆和第 4 堆的石子进行合并，如图所示：
4）选择第 4 堆和第 5 堆的石子进行合并，如图所示：

以上任意一种情况都会把石子变成 4 堆，然后就变成了求解 $4$ 堆石子的问题；我们可以采用同样方法，把石子变成 $3$ 堆， $2$ 堆，最后变成 $1$ 堆，从而求出问题的最终解。
当然，这是一个递归的过程，每次合并可以将石子堆数减一，总共进行 $n-1$ 次合并，每个阶段可行的方案数都是乘法的关系，穷举的方案总数就是 $(n-1)!$ ；
例如，上面提到的剩下的这 4 堆石子，采用深度优先搜索枚举所有可行解的搜索树如图所示：

图中用 ‘-’ 表示不同堆石子之间的分隔符，即 1-2-3-4 代表 4 堆的情况，12-3-4表示第 1 堆和第 2 堆合并后的情况。对这么多种方案取总消耗最小的，正确性是一定可以保证的，因为我们枚举了所有情况，然而时间上肯定是无法接受的。
那么，如何来优化搜索呢？我们发现这个问题的难点在于：当选出的两堆石子合并以后，它的重量变成了合并后的和，对于 $n$ 堆石子，选择的 $n-1$ 种合并方式，到达的都是不同的状态，无法进行状态存储。
当没有头绪的时候，我们试着将问题反过来思考；我们发现这棵深度优先搜索树的所有叶子结点都是一样的，这就为我们解决问题带来了突破口；对于 $[1, n]$ 堆石子，假设已经合并了 $n-2$ 次，必然只剩下二堆石子，那么我们只需要合并最后一次，就可以把两堆石子变成一堆，假设合并最后一次的位置发生在 $k$ ，也就是最后剩下两堆分别为： $[1, k]$ 和 $[k+1, n]$ ，如图二-2-1所示：注意，这个时候 $[1, k]$ 和 $[k+1, n]$ 已经各自合并成一堆了，所以我们把问题转换成了求 $[1, k]$ 合并一堆的最小消耗，以及 $[k+1, n]$ 合并成一堆的最小消耗；而这里 $k$ 的取值范围为 $[1, n-1]$ ；
利用这样的方法，逐步将区间缩小成 1，就可以得到整个问题的解了。令 $f[i][j]$ 表示从第 $i$ 堆石子到第 $j$ 堆石子合并成一堆所花费的最小代价。 $$f[i][j] = \begin{cases} 0 & i=j\ \min_{k=i}^{j-1}(f[i][k] + f[k+1][j] + cost(i,j)) & i \neq j\end{cases}$$
其中 $cost(i, j) = \sum_{k=i}^{j}w_k$
有了上面 “正难则反” 的解释，这个状态转移方程就很好理解了；
1）当 $i=j$ 时，由于 $f[i][j]$ 已经是一堆了，所以消耗自然就是 0 了；
2）当 $i \neq j$ 时，我们需要把目前剩下的两堆合并成一堆，一堆是 $f[i][k]$ ，另一堆是 $f[k+1][j]$ ，这两堆合并的消耗就是从第 $i$ 堆到第 $j$ 堆的重量之和，即 $cost(i, j) = \sum_{k=i}^{j}w_k$ ，而对于合并方案，总共 $k=j-i$ 种选择，所以枚举 $j-i$ 次，取其中最小值就是答案了。
通过记忆化搜索求解 $f[1][n]$ 就是最后的答案。
如图所示的动图，展示的是迭代求解的顺序，灰色的格子代表无效状态，红色的格子代表为长度为 2 的区间，橙色的格子代表为长度为 3 的区间，金黄色的格子则代表长度为 4 的区间，黄色的格子代表我们最终要求的区间状态，即 $f[1][5]$ 。

有关区间DP的更深入内容，可以参考：夜深人静写算法（二十七）- 区间DP。

九、数位DP

如果一个数的所有位数加起来是 $10$ 的倍数, 则称之为 $good \ number$ ，求区间 $[l, r](0 \le l \le r \le 10^{18})$ 内 $good \ number$ 的个数；

对于这个问题，朴素算法就是枚举区间里的每个数，并且判断可行性，时间复杂度为 $o((r-l)c)$ ， $c=19$ ，肯定是无法接受的。
对于区间 $[l, r]$ 内求满足数量的数，可以利用差分法分解问题；
假设 $[0, x]$ 内的 $good \ number$ 数量为 $g_x$ ，那么区间 $[l, r]$ 内的数量就是 $g_r - g_{l-1}$ ；分别用同样的方法求出 $g_r$ 和 $g_{l-1}$ ，再相减即可；

如果一个数字 $i$ 满足 $i < x$ ，那么 $i$ 从高到低肯定出现某一位，使得这一位上的数值小于 $x$ 对应位上的数值，并且之前的所有高位都和 $x$ 上的位相等。
举个例子，当 $x = 1314$ 时， $i=0abc$ 、 $i=12ab$ 、 $i=130a$ 、 $i=1312$ ，那么对于 $i$ 而言，无论后面的字母取什么数字，都是满足 $i < x$ 这个条件的。

如果我们要求 $g_{1314}$ 的值，可以通过枚举高位：当最高位为0，那么问题就转化成 $g_{999}$ 的子问题；当最高位为1，问题就转化成 $g_{314}$ 的子问题。
$g_{314}$ 可以继续递归求解，而 $g_{999}$ 由于每一位数字范围都是 $[0,9]$ ，可以转换成一般的动态规划问题来求解。

这里的前缀状态就对应了之前提到的 某些条件；
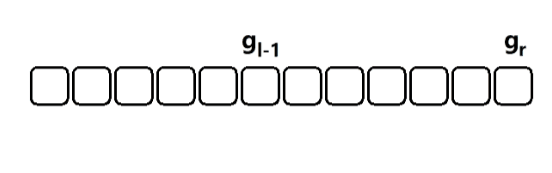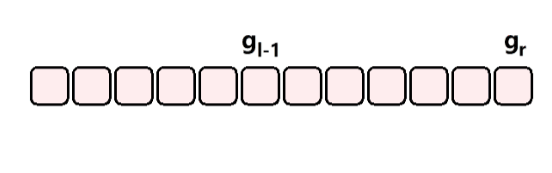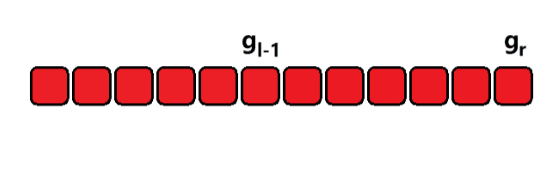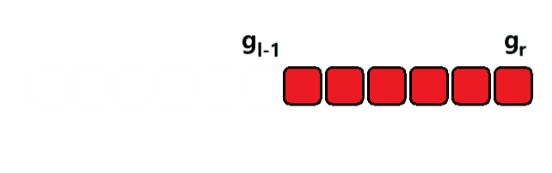
在这个问题中，前缀状态的描述为：一个数字前缀的各位数字之和对10取余（模）的值。前缀状态的变化过程如图所示：

在上题中，前缀状态的含义是：对于一个数 520 ，我们不需要记录 520 ，而只需要记录 7；对于 52013，我们不需要记录 52013，而只需要记录 1。这样就把原本海量的状态，变成了最多 10 个状态。
根据以上的三个信息，我们可以从高位到低位枚举数字 $i$ 的每一位，逐步把问题转化成小问题求解。
我们可以定义 $f(n, st, lim)$ 表示剩下还需要考虑 $n$ 位数字，前面已经枚举的高位组成的前缀状态为 $st$ ，且用 $lim$ 表示当前第 $n$ 位是否能够取到最大值（对于 $b$ 进制，最大值就是 $b-1$ ，比如 10 进制状态下，最大值就是 9）时的数字个数。我们来仔细解释一下这三维代表的含义：

1）当前枚举的位是 $n$ 位， $n$ 大的代表高位，小的代表低位；
2） $st$ 就是前缀状态，在这个问题中，代表了所有已经枚举的高位（即数字前缀）的各位数字之和对10取余（模）。注意：我们并不关心前缀的每一位数字是什么，而只关心它们加和模10之后的值是什么。
3） $lim=true$ 表示的是已经枚举的高位中已经出现了某一位比给定 $x$ 对应位小的数，那么后面枚举的每个数最大值就不再受 $x$ 控制；否则，最大值就应该是 $x$ 的对应位。举例说明，当十进制下的数 $x = 1314$ 时，枚举到高位前三位为 “131”， $lim = false$ ，那么第四位数字的区间取值就是 $[0,4]$ ；而枚举到高位前三位为 “130” 时， $lim = true$ ，那么第四位数字的区间取值就是 $[0, 9]$ 。
所以，我们根据以上的状态，预处理 $x$ 的每个数位，表示成十进制如下：

$x = d_nd_{n-1}...d_1$

(其中 $d_n$ 代表最高位， $d_1$ 代表最低位)
得出状态转移方程如下：

$\begin{aligned}& f(n, st, lim) \\ &= \sum_{k=0}^{maxv} f(n-1, (st+k) \mod 10, lim \ or \ (k < maxv))\end{aligned}$

$k$ 表示第 $n$ 位取什么数字，它的范围是 $[0, maxv]$ ；
$maxv$ 表示第 $n$ 位能够取到的最大值，它由 $lim$ 决定，即：

$maxv = \begin{cases}9 & lim = true\\d_n & lim = false\end{cases}$

利用上述的状态转移方程，我们可以进行递归求解，并且当 $n=0$ 的时候为递归出口，由于数字要求满足所有数字位数之和为 $10$ 的倍数，所以只有 $st = 0$ 的情况为合法状态，换言之，当 $n=0$ 时，有：

$f(0, x, lim) = \begin{cases} 1 & x = 0\\ 0 & 0 \lt x \le 9\end{cases}$

而我们需要求的，就是 $f(n, 0, false)$ 。
我们发现，如果按照以上的状态转移进行求解，会导致一个问题，就是会有很多重叠子问题，所以需要进行记忆化，比较简单的方法就是用一个三维数组 $f[n][st][lim]$ 来记忆化。
当然，这里有一个技巧，就是 $lim$ 这个变量只有 $true$ 、 $false$ 两种取值，并且当它为 $false$ 时，代表之前枚举的数的高位和所求区间 $[0, x]$ 右端点中的 $x$ 的高位保持完全一致，所以当 $lim = false$ 时，深度优先搜索树的分支最多只有 $1$ 条，所以无须记忆化，每次直接算就可以。如图二-3-2所示的蓝色结点，就是那条唯一分支。

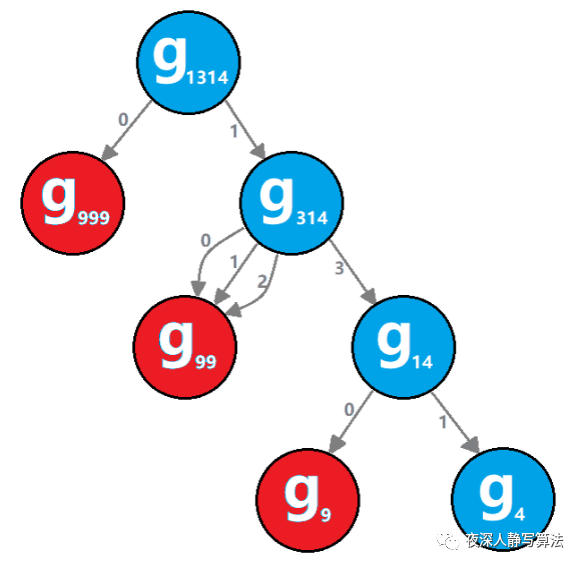
综上所述，我们只需要用 $f[n][st]$ 表示长度为 $n$ ，且每个数字的范围为 $[0, maxv]$ ，且前缀状态为 $st$ 的数字个数（这里 $maxv$ 和进制有关，如果是 $b$ 进制，那么 $maxv = b - 1$ ）。

$f(n, st, false)$ 采用普通深搜， $f(n, st, true)$ 采用记忆化搜索。
对于更加深入的数位DP的实现，可以参考：夜深人静写算法（二十九）- 数位DP。

十、状态压缩DP

给出 $graph$ 为有 $n(n \le 12)$ 个节点（编号为 0, 1, 2, …, $n-1$ ）的无向连通图。 $graph.length = n$ ，且只有节点 $i$ 和 $j$ 连通时， $j$ 不等于 $i$ 时且在列表 $graph[i]$ 中恰好出现一次。返回能够访问所有节点的最短路径的长度。可以在任一节点开始和结束，也可以多次重访节点，并且可以重用边。

这是一个可重复访问的旅行商问题。我们可以设计状态如下： $f(st, en, state)$ 代表从 $st$ 到 $en$ ，且 经过的节点 的状态组合为 $state$ 的最短路径。
状态组合的含义是：经过二进制来压缩得到的一个数字，比如 经过的节点 为 0、1、4，则 $state$ 的二进制表示为：

$(10011)_2$

即 经过的节点 对应到状态 $state$ 二进制表示的位为 1，其余位为 0。
于是，我们明确以下几个定义：初始状态、最终状态、非法状态、中间状态。

初始状态
初始状态一定是我们确定了某个起点，想象一下，假设起点在 $i$ ，那么在一开始的时候，必然 $state = 2^i$ 。于是，我们可以认为起点在 $i$ ，终点在 $i$ ，状态为 $2^i$ 的最短路径为 0。也就是初始状态表示如下：

$f(i, i, 2^i) = 0 \\ \ \\ i \in [0, n)$

最终状态
由于这个问题，没有告诉我们起点和终点，所以起点和终点是不确定的，我们需要通过枚举来得出，所以最终状态起点 $i$ 和终点 $j$ ，状态为 $2^n-1$ （代表所有点都经过，二进制的每一位都为 1）。最终状态表示为：

$f(i, j, 2^n-1) \\ \ \\ i \in [0, n), j \in [0, n)$

非法状态
非法状态就是 不可能从初始状态 通过 状态转移 到达的状态。我们设想一下，如果 $f(i, j, state)$ 中 $state$ 的二进制的第 $i$ 位为 0，或者第 $j$ 位为 0，则这个状态必然是非法的，它代表了两个矛盾的对立面。
我们把非法状态下的最短路径定义成 $inf = 10000000$ 即可。$$f(i, j, state) = inf$$
其中 (state & (1<<i)) == 0或者(state & (1<<j)) == 0代表state的二进制表示的第 $i$ 和 $j$ 位没有 1。

中间状态
除了以上三种状态以外的状态，都成为中间状态。

那么，我们可以通过 记忆化搜索，枚举所有的 $f(i, j, 2^n - 1)$ 的，求出一个最小值就是我们的答案了。状态数： $O(n^22^n)$ ，状态转移： $O(n)$ ，时间复杂度： $O(n^32^n)$ 。

十一、斜率DP

给定 $n(n \le 400000)$ 个数 $a_n$ ，现在需要将它们归类，每类至少 $t(1 < t \le n)$ 个数。归在同一类的花费为每个数字减去最小那个数字之和。希望所有数归类后的总花费最小，求这个最小花费。

首先贪心，排个序先。然后用 $sum[i]$ 代表前 $i$ 个数的和，其中 $sum[0]=0$ ， $dp[i]$ 代表前 $i$ 个数字归完类后的最小花费，则容易列出状态转移方程：

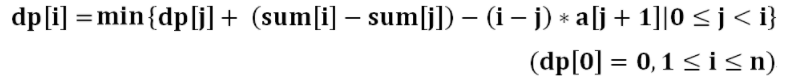
因为是排好序的，所以 $a[j+1]$ 是 $a[j+1:i]$ 这个区间内最小的那个数，这是个 $1D/1D$ 问题，即状态数为 $O(n)$ ，每个状态的转移成本为 $O(n)$ ，所以总的算法复杂度为 $O(n^2)$ 。朴素算法如下：

由于 $n$ 的范围太大，需要优化。算法优化的本质就是让上述代码的第一层循环不变，减少第二层循环的状态转移过程。首先将状态转移方程进行移项，得到如下等式：

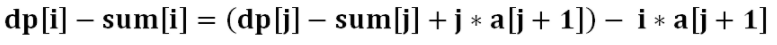
看上去貌似并没有什么变化，这么做的目的是什么呢？再来仔细看下这个式子：

这样一看，基本上就能看懂分类依据了，红色代表自变量为i的函数，绿色代表自变量为j的函数，蓝色则是以 $i$ 和 $j$ 为变量的函数，那么我们做进一步转化，使得该公式更加清晰。

将 $i$ 和 $j$ 为自变量的函数分别用b和y表示， $k=i$ 代表斜率。于是，状态转移方程转化成了以 $a[j+1]$ 为自变量， $i$ 为斜率， $dp[i]-sum[i]$ 为截距的直线方程。

如上图所示，当 $i$ 确定， $j$ 取 $t$ 时，则代表的是一条斜率为 $i$ ，并且过点 $T(a[t+1], dp[t]-sum[t]+t*a[t+1])$ 的直线。

更加一般地，当 $i$ 确定， $j$ 取不同值时，则这个平面上会出现一系列平行的直线，他们的斜率都是 $i$ 。因为 $i$ 是确定的，并且所有直线的斜率就是 $i$ ，所以所有直线相互平行；又由于 $j$ 的不同，直线经过不同的点，所以只要是两条不重合的平行直线，截距必然不同，而截距 $b=dp[i]-sum[i]$ ，即 $dp[i]=b+sum[i]$ ；所以可以得出结论：
dp[i]的最小值一定出现在最下面的那条直线上（因为最下面的直线截距最小）。
接下来，我们分析几条比较重要的性质：
第一条：维护“下凸”折线

如图所示，A、B、C三个点，其中B点位于AC直线之上，即为一个“上凸”点。然后我们连接AC两点，绘制所有的斜率小于K(A,C)的直线（图中绿色直线），发现截距最小的一定是经过点A的直线（想象一下，图中三根绿色的直线一起动起来的情况）；然后绘制所有的斜率大于K(A,C)的直线（图中红色直线），发现截距最小的一定是经过C的直线。于是，可以得出结论，在用A、B、C进行状态转移时，B永远是一个无用的状态转移。
由于任意三点不能出现“上凸”。所以，所有用于状态转移的点必须是一条“下凸”折线，如图所示：

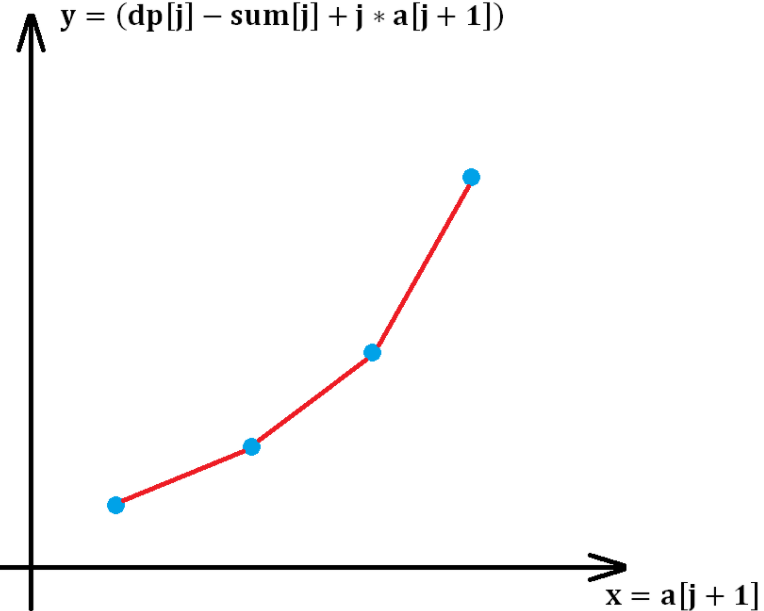
图中每个点都代表了向dp[i]进行状态转移的dp[j]。从图中可以看出，“下凸”折线满足每段折线斜率单调递增。那么如何维护这段“下凸”折线？
我们采用双端队列来维护，由于它存储结构的单调性（斜率单调），又称为“单调队列”。deq[]代表单调队列的数据域，head和tail分别表示它的两个指针，当 head和tail相等则代表单调队列为空，初始化head=tail=0。deq[]中的每个元素存的是原数组的下标，因为通过下标就能计算出坐标图中点的 x-y坐标，也就能计算相邻两点之间的斜率了。
那么每次我们将一个可行的转移状态j放入单调队列之前，先判断它的加入能否保证斜率单调递增，如果不能则将单调队列尾元素删除，依次往复，最后将这个点放入单调队列尾部，这样一条“下凸”折线就算维护完毕了。
细心的读者，会发现这一步操作同样可以用“栈”这种数据结构来完成。接下来，我们继续来探讨为什么用双端队列不用栈。
第二条：“永不录用”点的剔除
“永不录用”这个名字是我自己起的，那么哪些点是“永不录用”点？，还是来看图：

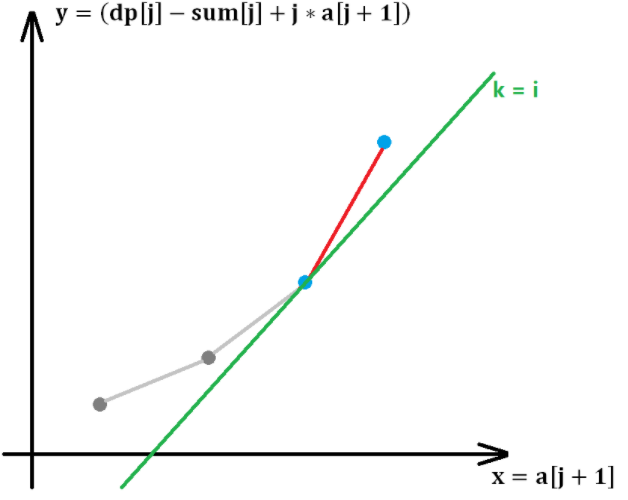
由于每次枚举状态i时是递增的枚举（之前那段代码的第一个for循环），也就是说斜率一定是越来越大，那么从图中可以看出，那些斜率小于i的折线上的点（灰色点）如果要经过斜率为i的直线（图中绿色直线的平行线），则产生的截距必然不会比图中绿色直线的更小，也就是灰色点都可以删除了。
这些可以删除的灰色点就是“永不录用”点。“永不录用”点更加官方的说法，就是单调队列里的折线中，所有斜率小于i的折线的左端点。由于单调队列的斜率单调性，所以删除点的操作可以从左往右进行，这就是为什么之前不用栈来维护的根本原因。如果维护折线用的是栈，则最左边的点势必在栈底，而栈这种数据结构只能获取栈顶元素。