[Python人工智能] 三.TensorFlow基础之Session、变量、传入值和激励函数 丨【百变AI秀】
从本篇文章开始,作者正式开始研究Python深度学习、神经网络及人工智能相关知识。前一篇文章讲解了TensorFlow基础和一元直线预测的案例;本篇文章将详细介绍Session、变量、传入值和激励函数。主要结合作者之前的博客和"莫烦大神"的视频介绍,后面随着深入会讲解具体的项目及应用。
基础性文章,希望对您有所帮助,如果文章中存在错误或不足之处,还请海涵~文章最初想以TensorFlow2.0撰写,但更改太多,而且自己也是初学者,所以想先学深入后续再补充2.0相关知识。同时自己作为人工智能的菜鸟,希望大家能与我在这一笔一划的博客中成长起来,共勉。
前文赏析:
- [Python人工智能] 一.TensorFlow2.0环境搭建及神经网络入门
- [Python人工智能] 二.TensorFlow基础及一元直线预测案例
- [Python人工智能] 三.TensorFlow基础之Session、变量、传入值和激励函数 丨【百变AI秀】
代码下载地址(欢迎大家关注点赞):
一.tensor张量
TensorFlow中文翻译是“向量飞舞”,这也是TensorFlow的基本含义。Tensorflow使用数据流图(data flow graphs)技术来进行数值计算。数据流图是一个有向图,使用节点(一般用圆形或方形描述,表示一个数学操作或数据输入的起点和数据输出的终点)和线(表示数字、矩阵或Tensor张量)来描述数学计算。数据流图可以方便的将各个节点分配到不同的计算设备上完成异步并行计算,非常适合大规模的机器学习应用。如下图所示,通过Gradients不断学习改进我们的权重W和偏置b,从而提升准确度。

Tensor(张量)是tensorflow框架使用的基本数据结构,张量即多维数组,在python中可以理解为嵌套的多维列表。张量的维度称为阶,0阶张量又称为标量,1阶张量又称为向量,2阶张量又称为矩阵。
# 0阶张量 标量
5
# 1阶张量 向量大小为3
[1., 2., 3.]
# 2阶张量 2*3矩阵
[[1., 2., 3.],
[4., 5., 6.]]
# 3阶张量 大小为2*3*2
[[[1., 2.],[3., 4.],[5., 6.]],
[[7., 8.],[9., 10.],[11., 12.]]]
代码如下:
# -*- coding: utf-8 -*-
import tensorflow as tf
#定义变量
a = tf.constant([1, 2, 3], name="a")
b = tf.constant([[1, 2, 3],[4, 5, 6]])
print(a)
print(b)
#创造数组0和1
c = tf.zeros([2, 3])
d = tf.ones([2,3])
print(c)
print(d)
#随机生成一个正态分布
e = tf.random.normal([5,3])
print(e)
输出结果如下图所示:

二.Session
Tensor实际上就是一个多维数组,是TensorFlow的主要数据结构。它们在一个或多个由节点(nodes)和边(edges)组成的图(graphs)中流动。边代表的是tensors,节点代表的是对tensors的操作(operations)。tensors在图中从一个节点流向另一个节点,每次经过一个节点都会接受一次操作。
此外,图必须在会话里被启动,会话将图的操作分发到CPU或GPU之类的设备上,同时提供执行操作(op)的方法,这些方法执行后,将产生的tensor返回。TensorFlow程序通常被组织成一个构建阶段和一个执行阶段:
- 在构建阶段,op的执行步骤被描述成一个图
- 在执行阶段,使用会话执行图中的op
比如,在构建阶段创建一个图来表示和训练神经网络,然后在执行阶段反复执行图中的训练op。TensorFlow中涉及的运算都要放在图中,而图的运行只发生在会话(session)中。开启会话后,就可以用数据去填充节点,并进行运算;关闭会话则不能进行计算。会话提供了操作运行和Tensor求值的环境。
下面举一个简单的例子。我们使用Session对象的run()方法来执行乘法操作,定义两个矩阵matrix1和matrix2,然后再Session中运行。
# -*- coding: utf-8 -*-
"""
Created on Sat Nov 30 16:38:31 2019
@author: Eastmount CSDN YXZ
"""
import tensorflow as tf
# 建立两个矩阵
matrix1 = tf.constant([[3,3]]) #常量 1行2列
matrix2 = tf.constant([[2],
[2]]) #常量 2行1列
# 矩阵乘法 matrix multiply 类似于numpy.dot()函数
product = tf.matmul(matrix1, matrix2)
# 两种利用Session会话控制的方法
# 方法一
sess = tf.Session()
output = sess.run(product) # 执行操作 每run一次TensorFlow才会执行操作
print(output)
sess.close()
# 方法二
with tf.Session() as sess: # 打开Session并且赋值为sess 运行结束会自动close
output = sess.run(product)
print(output)
输出结果如下所示:
[[12]]
[[12]]
三.常量和变量
在TensorFlow中,使用tf.constant来创建常量。
# 创建1*2矩阵常量
c1 = tf.constant([[1., 1.]])
# 创建2*1矩阵常量
c2 = tf.constant([[2.],[2.]])
在TensorFlow中,使用tf.Variable来创建变量。变量(Variable)是特殊的张量,它的值可以是一个任何类型和形状的张量。其中,变量的定义和Python中不太一样,比如state = tf.Variable(),TensorFlow必须要定义成一个变量,它才是一个真正的变量。
# 创建一个0阶变量并初始化为0
state = tf.Variable(0, name='counter')
创建变量时,必须将一个张量作为初始值传入构造函数Variable(),TensorFlow提供了一系列操作符来初始化张量如tf.random_normal和tf.zeros。
# 标准差为0.35的正态分布初始化一个形状(10,20)的变量
w = tf.Variable(tf.random_normal([10, 20], stddev=0.35), name="w")
接着实现一个案例,循环输出变量。该代码需要注意:
- 定义变量一定要初始化,使用global_variables_initializer() 或 initialize_all_variables()
- 定义Session时一定要使用sess.run(init)初始化,然后才能使用
# -*- coding: utf-8 -*-
"""
Created on Sun Dec 1 16:52:18 2019
@author: Eastmount CSDN YXZ
"""
import tensorflow as tf
# 定义变量 初始值为0 变量名字为counter(用于计数)
state = tf.Variable(0, name='counter')
print(state.name)
print(state)
# 定义常量
one = tf.constant(1)
print(one)
# 新变量
result = tf.add(state, one)
# 更新: result变量加载到state中 state当前变量即为result
update = tf.assign(state, result)
# Tensorflow中需要初始化所有变量才能激活
init = tf.global_variables_initializer() # must have if define variable
# Session
with tf.Session() as sess:
sess.run(init)
# 三次循环更新变量
for _ in range(3):
sess.run(update)
print(sess.run(state)) #直接输出state没用 需要run
循环最开始执行sess.run(update),此时的state会加1输出,接着继续执行两次输出2、3。
1
2
3
继续补充一个案例,
import tensorflow as tf
# 定义变量
a = tf.constant([5, 3], name='input_a')
# 计算
b = tf.reduce_prod(a, name='prod_b')
c = tf.reduce_sum(a, name='sum_c')
d = tf.add(b, c, name='add_d')
# Session
with tf.Session() as sess:
print('a:', sess.run(a))
print('b:', sess.run(b))
print('c:', sess.run(c))
print('d:', sess.run(d))
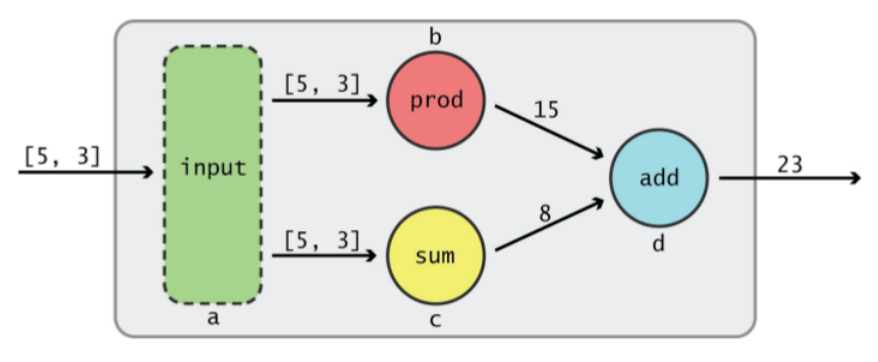
输出结果如下图所示,节点a接收了一个tensor,该tensor从节点a流出后,分别流向了节点b和c,节点b执行的是prod操作5*3,节点c执行的是sum操作5+3。当tensor从节点b流出时变成了15,从节点c流出时变成了8。此时,2个tensor又同时流入节点d,接受的是add操作15+8,最后从节点d流出的tensor就是23。
a: [5 3]
b: 15
c: 8
d: 23
tensor是在graph中流动的过程如下图所示。当我们把图中的一个节点传递给Session.run( )的时候,实际上就是在对TensorFlow说“Hi,我想要这个node的输出,请帮我运行相应的操作来得到它,谢谢!” 这时,Session会找到这个node所依赖的所有操作,然后按照从前到后的顺序依次进行计算,直到得出你所需要的结果。
四.placeholder传入值
placeholder称为传入值或占位符。上述示例在计算图中引入了张量,以常量或变量的形式存储,Tensorflow中还提供了另外一种机制,即先定义占位符,等到真正执行的时候再用具体值去填充或更新占位符的值。
TensorFlow使用tf.placeholder()创建占位符,开始先hold住变量,之后会从外界传入进来,把placeholder值填充进去,Session.run的feed_dict为参数填充值。
# -*- coding: utf-8 -*-
"""
Created on Sun Dec 1 18:21:29 2019
@author: Eastmount CSDN YXZ
"""
import tensorflow as tf
# 传入值 给定type
input1 = tf.placeholder(tf.float32)
input2 = tf.placeholder(tf.float32)
# 输出 乘法运算
output = tf.multiply(input1, input2)
# Session
with tf.Session() as sess:
# placeholder需要传入值,在session.run时传入字典类型
print(sess.run(output, feed_dict={input1:[7.], input2:[2.0]}))
输出结果如下所示,如果你要用placeholder,就意味着你想在运行结果的时候在给输入值。
[14.]
五.激励函数
激励函数(activation function)会让某一部分神经元先激活,然后把激活的信息传递给后面一层的神经系统中。比如,某些神经元看到猫的图片,它会对猫的眼睛特别感兴趣,那当神经元看到猫的眼睛时,它就被激励了,它的数值就会被提高。
激励函数相当于一个过滤器或激励器,它把特有的信息或特征激活,常见的激活函数包括softplus、sigmoid、relu、softmax、elu、tanh等。对于隐藏层,我们可以使用relu、tanh、softplus等非线性关系;对于分类问题,我们可以使用sigmoid(值越小越接近于0,值越大越接近于1)、softmax函数,对每个类求概率,最后以最大的概率作为结果;对于回归问题,可以使用线性函数(linear function)来实验。常见的激励函数参考维基百科:https://en.wikipedia.org/wiki/Activation_function
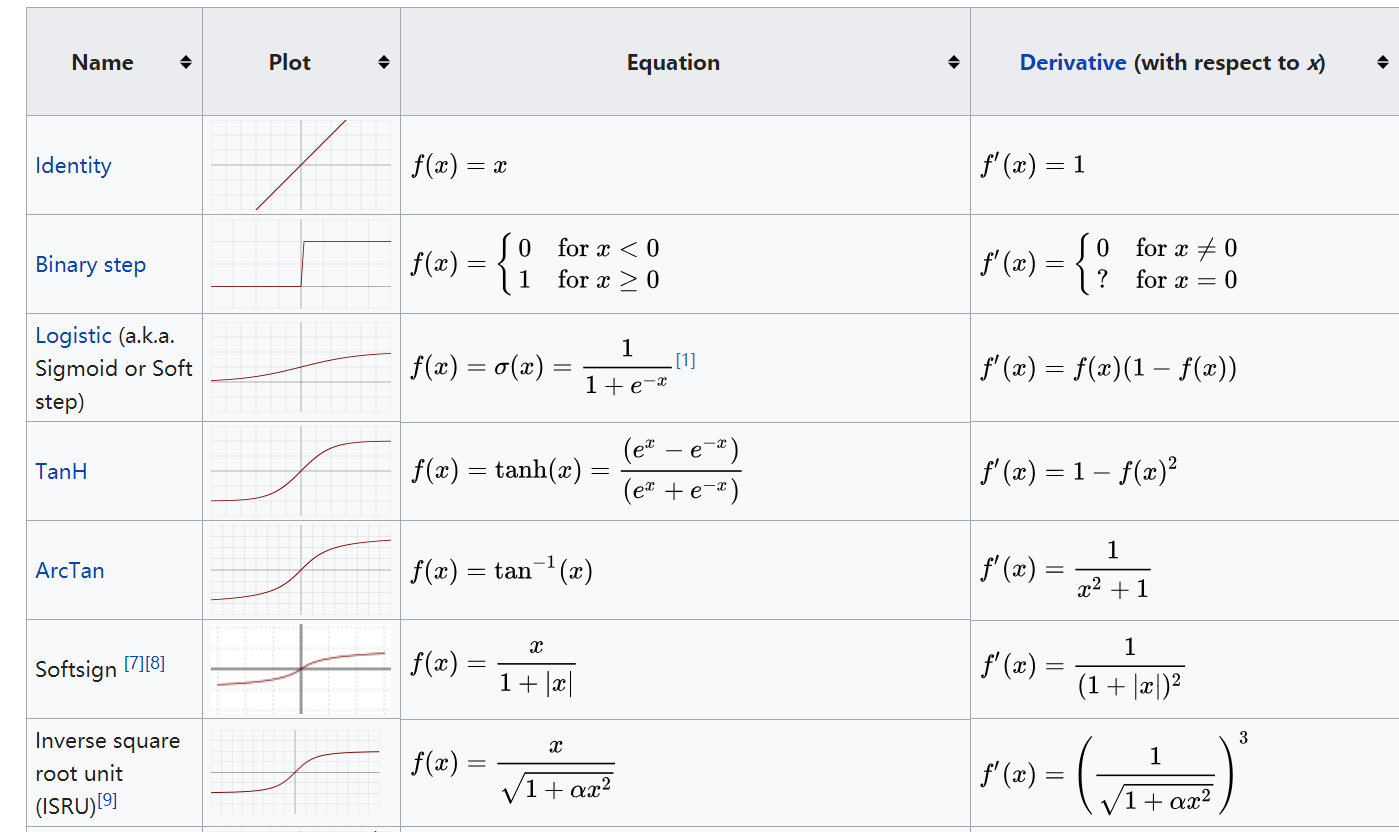
TensorFlow的结构如下,输入值input经过隐藏层layer1和layer2,然后有一个预测值predictions。cross_entropy是计算跟真实值的差距。
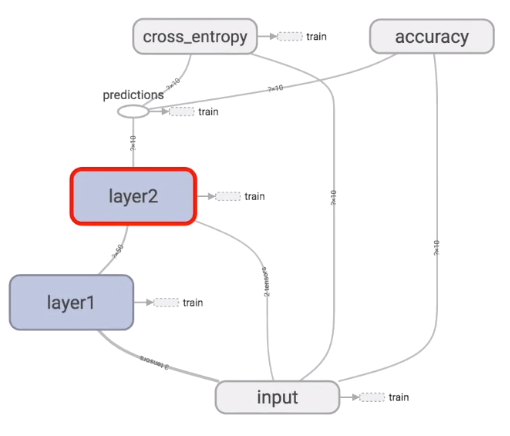
打开layer2,可以看到激励函数在这里面。layer1传进来的值进行加工,加工完之后layer2要输出值Wx_plus_b,该值经过一个激励函数relu,某些部分被激励,然后继续传递到predictions作为预测值。
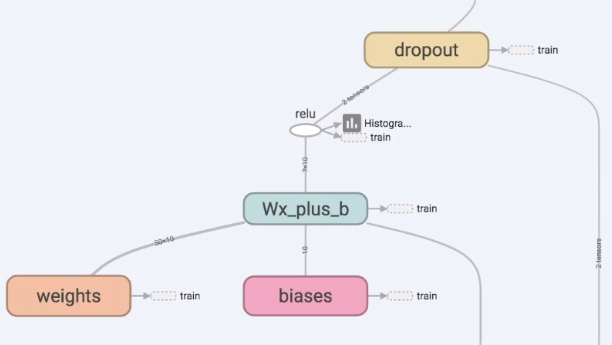
也可以在google或baidu搜索“TensorFlow activation”,激励函数显示如下图所示:
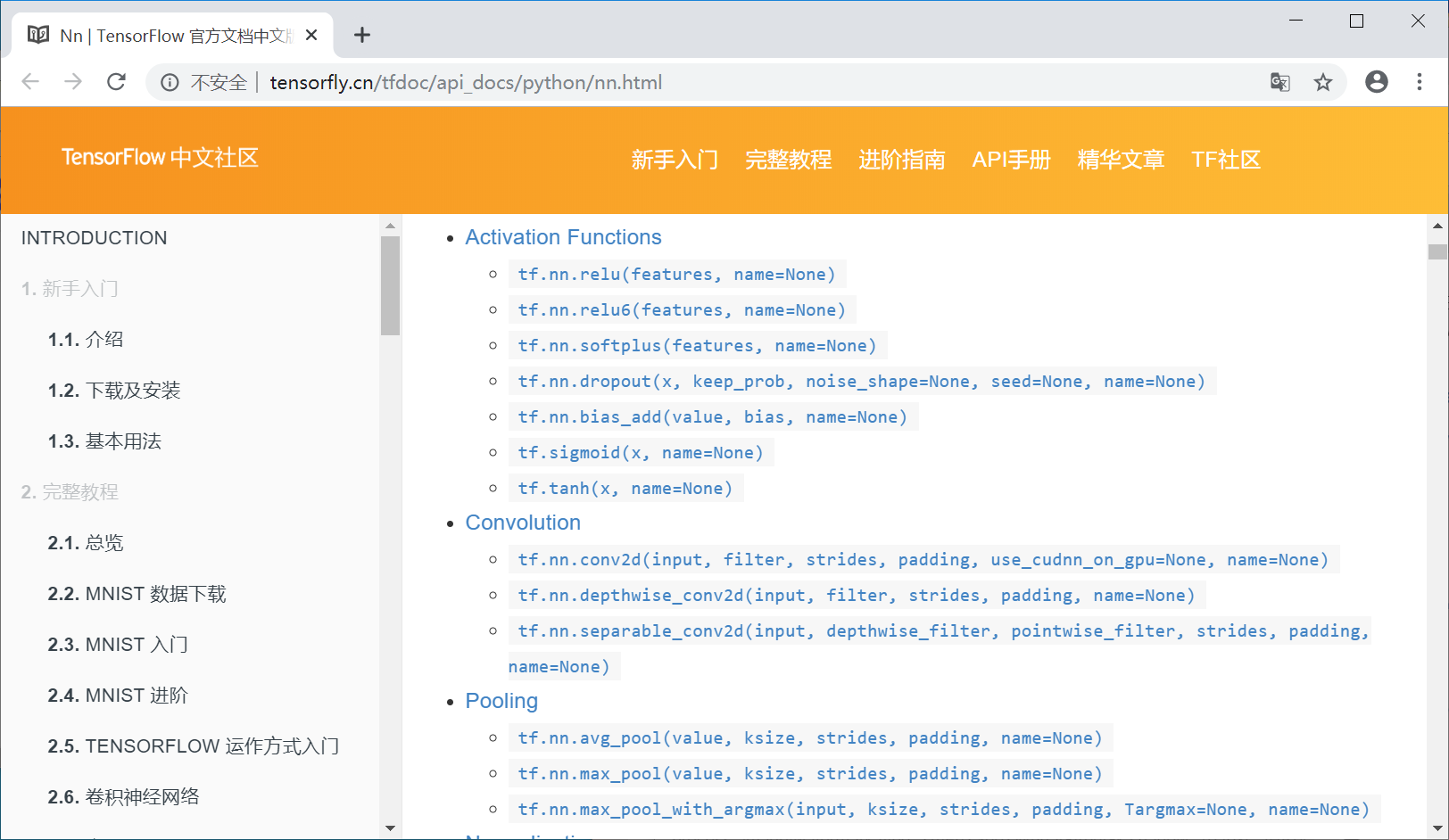
下面补充一个简单的激励函数例子,后续我们会结合具体的案例来运用激励函数解决实际的问题。
import tensorflow as tf
a = tf.constant([-1.0, 2.0])
# 激励函数
with tf.Session() as sess:
b = tf.nn.relu(a)
print(sess.run(b))
c = tf.sigmoid(a)
print(sess.run(c))
输出结果为:
[0. 2.]
[0.26894143 0.880797 ]
其中Sigmoid函数为:
\displaystyle S(x)={\frac {1}{1+e^{-x}}}
这是传统神经网络中最常用的激活函数之一,优点是它输出映射在(0,1)内,单调连续,非常适合用作输出层,并且求导比较容易。缺点是具有软饱和性,一旦输入落入饱和区,一阶导数就变得接近于0,很容易产生梯度消失。
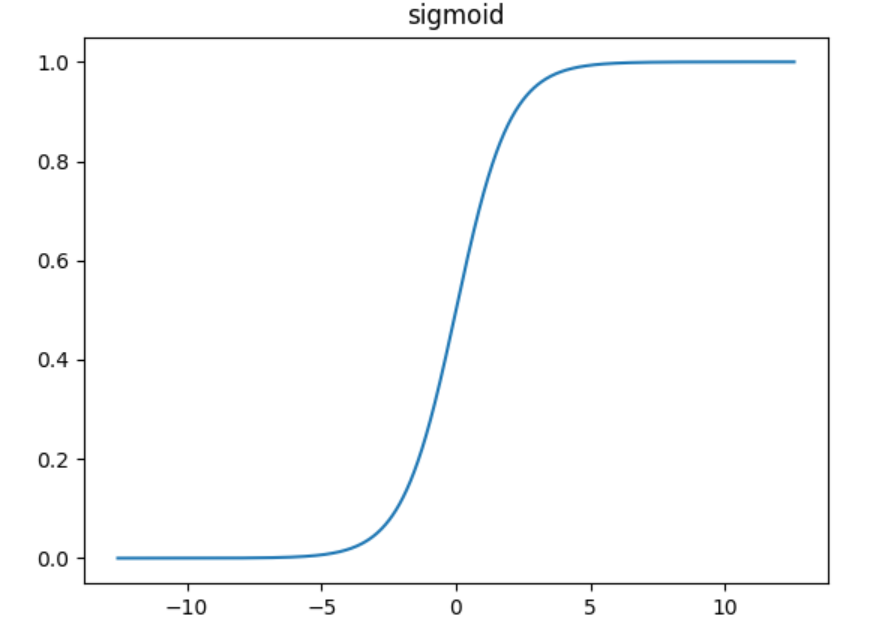
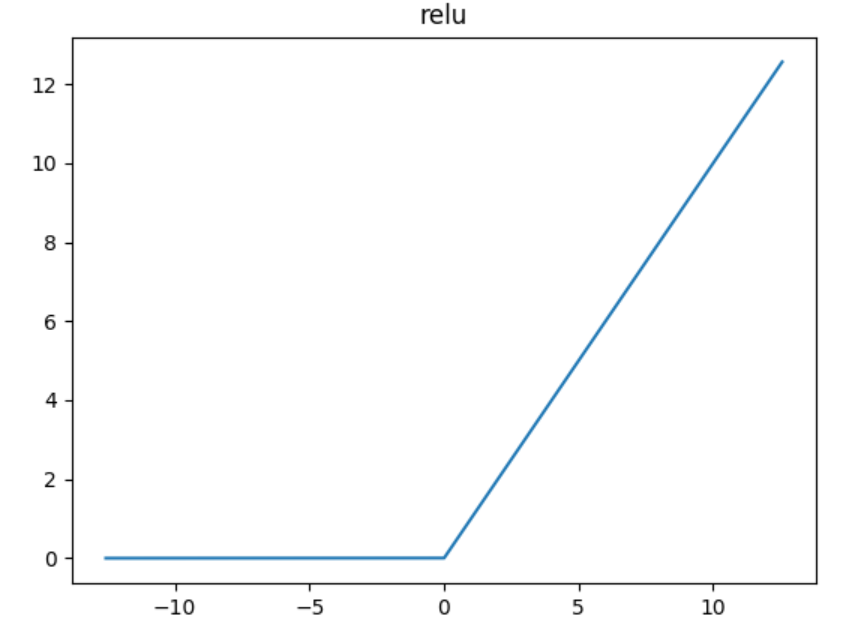
relu函数是目前用的最多也是最受欢迎的激活函数。公式和函数图像如下:
f(x) = max(x, 0)
由图可知,relu在x<0时是硬饱和,由于当x>0时一阶导数为1。所以,relu函数在x>0时可以保持梯度不衰减,从而缓解梯度消失问题,还可以更快的去收敛。但随着训练进行,部分输入会落到硬饱和区,导致对应的权重无法更新。
六.总结
写到这里,这篇基础性的TensorFlow文章就讲述完毕。这是非常基础的一篇深度学习文章,同时文章中存在错误或不足之处,还请海涵~同时,作为人工智能的菜鸟,我希望自己能不断进步并深入,后续将它应用于图像识别、网络安全、对抗样本等领域,一起加油!女神晚上收到了又一封家书,道不尽的思恋,读博不易,写文也不易,且行且珍惜。

感恩能与大家在华为云遇见!
希望能与大家一起在华为云社区共同成长。原文地址:https://blog.csdn.net/Eastmount/article/details/103336214
【百变AI秀】有奖征文火热进行中:https://bbs.huaweicloud.com/blogs/296704
(By:娜璋之家 Eastmount 2021-09-04 夜于武汉)
参考文献:
[1] 神经网络和机器学习基础入门分享 - 作者的文章
[2] 斯坦福机器学习视频NG教授: https://class.coursera.org/ml/class/index
[3] 书籍《游戏开发中的人工智能》、《游戏编程中的人工智能技术》
[4] 网易云莫烦老师视频(强推 我付费支持老师一波):https://study.163.com/course/courseLearn.htm?courseId=1003209007
[5] 神经网络激励函数 - deeplearning
[6] tensorflow架构 - NoMorningstar
[7] 《TensorFlow2.0》低阶 api 入门 - GumKey
[8] TensorFlow之基础知识 - kk123k
[9] Tensorflow基础知识梳理- sinat_36190649
[10] 深度学习之 TensorFlow(二):TensorFlow 基础知识 - 希希里之海
[11] tensorflow基础概念 - lusic01
[12] tensorflow:激活函数(Activation Function) - haoji007
[13] AI => Tensorflow2.0语法 - 张量&基本函数(一)
- 点赞
- 收藏
- 关注作者


评论(0)