【 FPGA 】16点并行DIT FFT的实现
目录
整体架构介绍
16点并行FFT分为4级蝶形运算,每一级蝶形运算有一个基本的蝶形单元:

如下是16点DIT FFT的数据流图:

可见,第0级蝶形运算的输入的顺序是:
x(0)、x(8)、x(4)、x(12)、x(2)、x(10)、x(6)、x(14)、x(1)、x(9)、x(5)、x(13)、x(3)、x(11)、x(7)、x(15);
只有这样排列输入,才能得到最终顺序的输出:
x(0)、x(1)、x(2)、x(3)、x(4)、x(5)、x(6)、x(7)、x(8)、x(9)、x(10)、x(11)、x(12)、x(13)、x(14)、x(15);
旋转因子介绍
蝶形因子通用的表示为: ,从DIT FFT的数据流图可以看出,第0级蝶形运算的旋转因子为
,从DIT FFT的数据流图可以看出,第0级蝶形运算的旋转因子为 ;第1级蝶形运算的旋转因子为:
;第1级蝶形运算的旋转因子为: ,
, ;第2级蝶形运算的蝶形因子为:
;第2级蝶形运算的蝶形因子为: ,
, ,
, ,
, ;第3级蝶形运算的蝶形因子为:
;第3级蝶形运算的蝶形因子为: ,
, ,
, ,
, ,
, ,
, ,
, ,
, 。
。
那么这些蝶形因子在Verilog中如何表示呢?
 ,这样的话:
,这样的话:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
如此:
第0级蝶形因子:
 ;
;
第1级蝶形因子:
 ;
;
 ;
;
第2级蝶形因子:
 ;
;
 ;
;
 ;
;
 ;
;
第3级蝶形因子:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
在Verilog设计中,蝶形因子肯定要使用parameter来定义,定义成参数,如何去做呢?
FPGA擅长进行定点数的运算,所以,我们要想办法将上述蝶形因子进行扩大,例如扩大512倍,得到:
第0级蝶形因子:
 ;
;
第1级蝶形因子:
 ;
;
 ;
;
第2级蝶形因子:
 ;
;
 ;
;
 ;
;
 ;
;
第3级蝶形因子:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
蝶形因子虽然扩大了,但是后面运算还需要注意了,保证同时扩大,同时缩小,得到最终正确结果。
代码文件结构
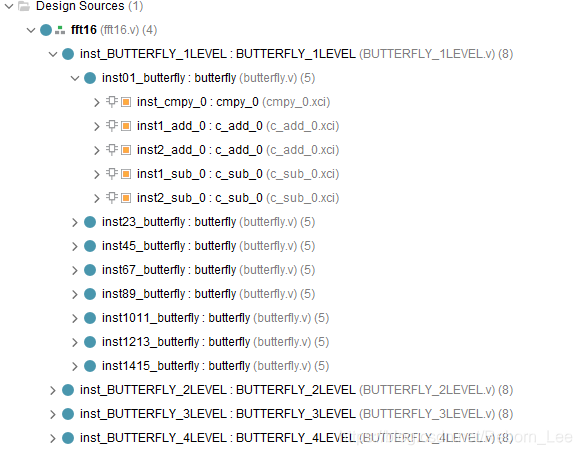
我们对这个16点并行FFT算法进行描述的时候,采用的结构是从层层例化,从该算法的最顶层fft16,到4级蝶形运算,以及每级蝶形运算包含的8个蝶形单元,在到蝶形单元里面的复数乘法,加法器,减法器等等。从顶层开始描述到最底层,到达最底层,其实只用到了一个复数乘法器,一个加法器,一个减法器。蝶形因此采用参数的方式进行传递。
我的程序结构:

蝶形单元用的是IP核:
仿真文件结构:
仿真源统一命名,test_要测试的module;
仿真结果结构:
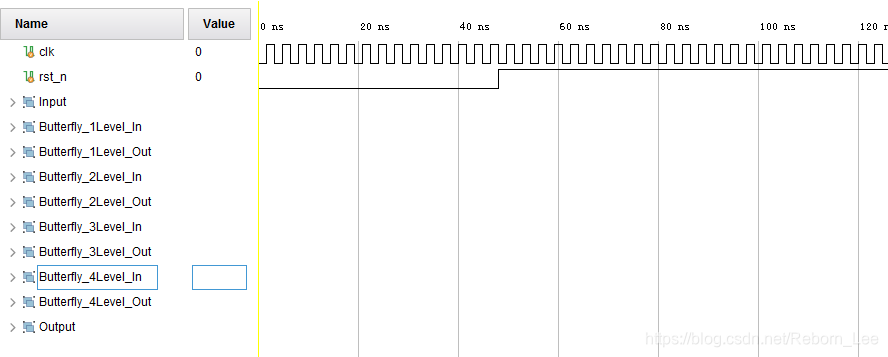
对输入输出建立分组,分组观察每一级输入输出信号,确保输入输出连贯,不要中间某一级输入输出异常,以及前一级与后一级输出输入不对应的错误。
具体要看某一级信号:

重点难点易错点
下面总结的都是个人遇到的问题,不代表你会如此。
重点:是对于蝶形因子的处理,以及代码风格的处理,争取不在顶层多写一行代码,通过层层例化,让代码结构一目了然,易于升级与维护。
难点:在与对每一级结果的位数的处理,每一级的结果如何进行截位,输出位宽设计为多少能够满足要求等等。
另一个难点永远都在于代码的调试,debug耗时耗力,进度跟不上的压力等等。
易错点:
易错点在于仿真时候如何给第一级蝶形运算输入数据,注意第一级蝶形运算的数据并不是顺序排列,而是有一定的规律。
仿真的结果如何判断呢?
可以借助Matlab,例如:
>> a = real(fft([0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0]))
>> b = imag(fft([0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0]))
输入是16点数据,输出是怎么样的呢?
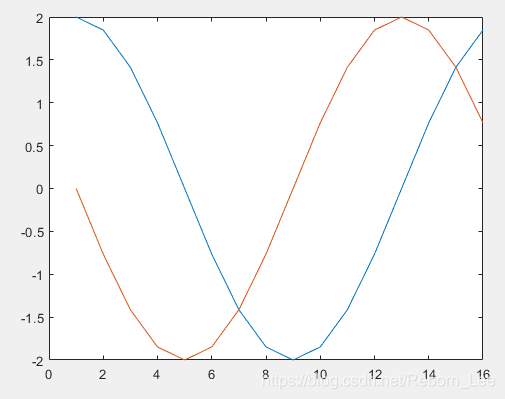
输出呈现出余弦波形的规律,可以定性的进行比较。
心里有个大概。
文章来源: reborn.blog.csdn.net,作者:李锐博恩,版权归原作者所有,如需转载,请联系作者。
原文链接:reborn.blog.csdn.net/article/details/102638821
- 点赞
- 收藏
- 关注作者


评论(0)